Parametric equations and and a parameter interval for the motion of a particle in the xy-plane are given. Identify the particle's path by finding a Cartesian equation for it. Graph the Cartesian equation. Indicate the portion of the graph
traced by the particle and the direction of motion.
- 
A) ; Counterclockwise from to one rotation 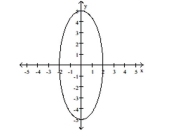
B) ; Counterclockwise from , to , one rotation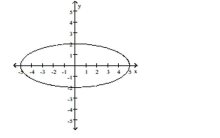
C) ; Counterclockwise from to , one rotation 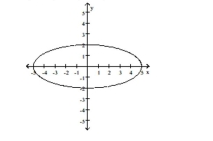
D) ; Counterclockwise from to , one rotation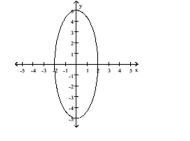
Correct Answer:
Verified
Q4: Graph the pair of parametric equations
Q5: Graph the pair of parametric equations
Q6: Graph the pair of parametric equations
Q7: Parametric equations and and a parameter
Q8: Parametric equations and and a parameter
Q10: Parametric equations and and a parameter
Q11: Find a parametrization for the curve.
-The ray
Q12: Graph the pair of parametric equations
Q13: Graph the pair of parametric equations
Q14: Graph the pair of parametric equations
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents