Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 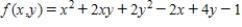
A) 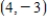 is the point of maximum, 11 is the relative maximum
is the point of maximum, 11 is the relative maximum
B)  is the critical point, it is impossible to determine the relative extrema of the function
is the critical point, it is impossible to determine the relative extrema of the function
C) 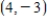 is the point of minimum, -11 is the relative minimum
is the point of minimum, -11 is the relative minimum
D) 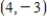 is the critical point, the function has neither a relative maximum nor a relative minimum at this point
is the critical point, the function has neither a relative maximum nor a relative minimum at this point
E) no critical points
Correct Answer:
Verified
Q143: Find the critical point(s) of the function.
Q144: Find the critical point(s) of the function.
Q145: Find the critical point(s) of the function.
Q146: Find the critical point(s) of the function.
Q147: Determine whether the statement is true or
Q149: Find the critical point(s) of the function.
Q150: Find the equation of the least-squares line
Q151: Determine whether the statement is true or
Q152: Find the critical point(s) of the function.
Q153: Find the critical point(s) of the function.
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents