Solved

A Covariance Stationary Time Series Is Weakly Dependent If

Question 20

Multiple Choice

A covariance stationary time series is weakly dependent if:


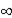A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . 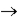as h A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . 0.
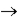
B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . 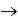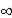A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . .
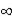C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . .
D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . as h A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . A covariance stationary time series is weakly dependent if: A) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to as h 0. B) the correlation between the independent variable at time 't' and the dependent variable at time 't + h' goes to 0 as h . C) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to 0 as h . D) the correlation between the independent variable at time 't' and the independent variable at time 't + h' goes to as h . .

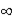Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q15: Unit root processes, such as a random

Q16: Covariance stationary sequences where Corr(xt + xt+h)

Q17: If ut refers to the error term

Q18: Which of the following is assumed in

Q19: The model yt = et +

Q21: The homoskedasticity assumption in time series regression

Q22: If a process is a covariance stationary

Q23: Which of the following is true if

Q24: Under adaptive expectations, the expected current value

Q25: The first difference of an I(1) time

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents