Find the smallest positive integer and the largest negative integer that, by the Upper- and Lower-Bound Theorem, are upper and lower bounds, respectively, for the real zeros of the polynomial function 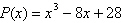 .
.
A) upper bound 3, lower bound -4
B) upper bound 20, lower bound -28
C) upper bound 28, lower bound -28
D) upper bound 4, lower bound -1
E) upper bound 20, lower bound -20
Correct Answer:
Verified
Q16: Sketch the graph of the polynomial function
Q17: Determine the value of k so that
Q18: Determine the x -intercepts of the graph
Q19: The number of ways you can select
Q20: Determine the x -intercepts of the graph
Q22: Find the smallest positive integer and the
Q23: Find the zeros of the polynomial function
Q24: Find all of the zeros of the
Q25: A company constructs boxes from rectangular pieces
Q26: A cube measures n inches on each
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents