A tank contains 200 litres of fluid in which 60 grams of salt is dissolved. A brine solution of 2 grams of salt per litre is pumped into the tank at a rate of 2 litres/minute. The well-stirred solution is then pumped out at the same rate.(a) Write the differential equation in terms of Q(t) and t and write the initial condition to model this problem. (Q(t) should represent the amount of salt in the tank at time t.) (b) Solve the equation in part (a) .(c) How much salt will be present in the tank after a long period of time?
A) (a)  = 2 -
= 2 - 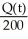 , Q(0) = 60 (b) Q(t) = 200 - 340
, Q(0) = 60 (b) Q(t) = 200 - 340 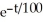 (c) 200 grams
(c) 200 grams
B) (a)  = 4 -
= 4 - 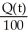 , Q(0) = 60 (b) Q(t) = 400 - 340
, Q(0) = 60 (b) Q(t) = 400 - 340  (c) 400 grams
(c) 400 grams
C) (a) 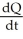 = 400 -
= 400 - 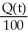 , Q(0) = 60 (b) Q(t) = 40 - 34
, Q(0) = 60 (b) Q(t) = 40 - 34 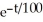 (c) 40 grams
(c) 40 grams
D) (a) 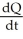 = 400 -
= 400 - 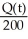 , Q(0) = 60 (b) Q(t) = 4 - 3.4
, Q(0) = 60 (b) Q(t) = 4 - 3.4  (c) 4 grams
(c) 4 grams
E) (a) 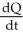 = 200 -
= 200 - 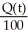 , Q(0) = 60 (b) Q(t) = 20 - 34
, Q(0) = 60 (b) Q(t) = 20 - 34 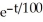 (c) 20 grams
(c) 20 grams
Correct Answer:
Verified
Q35: Find a general solution to the first
Q36: Find the general solution of the differential
Q37: Solve the initial-value problem Q38: Solve the differential equation Q39: Solve the differential equation (3y + 8x Q41: Solve the following initial-value problem:cos(x) Q42: Use Euler's method to determine an approximate Q43: Use Euler's method to determine an approximate Q44: Use the Euler method to determine an Q45: Use Euler's method with step size h![]()
![]()
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents