Solved

Let and F Be Sufficiently Smooth Scalar and Vector Fields

Question 35

Multiple Choice

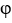Let Let and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity . ( F ) = ( ) . F + ( . F) using the notations grad , div or curl. A) curl ( F) = grad ( ) . F + div (F) B) div ( F) = curl ( ) . F + grad (F) C) div ( F) = grad ( ) . F + div (F) D) grad ( F) = div ( ) . F + curl (F) E) curl ( F) = div ( ) . 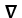F + grad (F) and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity Let and F be sufficiently smooth scalar and vector fields, respectively.Express the well-known identity . ( F ) = ( ) . F + ( . F) using the notations grad , div or curl. A) curl ( F) = grad ( ) . F + div (F) B) div ( F) = curl ( ) . F + grad (F) C) div ( F) = grad ( ) . F + div (F) D) grad ( F) = div ( ) . F + curl (F) E) curl ( F) = div ( ) . F + grad (F) . (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F ) = (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 ) . F + 11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 (11ee7bad_7817_372f_ae82_a36163e56c30_TB9661_11. F) using the notations grad , div or curl.


A) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
B) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = curl (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 grad (F)
C) div (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = grad (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 div (F)
D) grad (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 curl (F)
E) curl (11ee7bad_9f85_f900_ae82_29e1b84eee54_TB9661_11 F) = div (11ee7bad_e8b4_1a82_ae82_cd578f612ee6_TB9661_11 ) . F + 11ee7bad_d4f5_2c01_ae82_0ffef783bd40_TB9661_11 grad (F)

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q30: Find all values of the nonzero

Q31: Verify that the vector field F =

Q32: For what value of the constant C

Q33: Show that there does not exist

Q34: A vector field F satisfying the equation

Q36: Every conservative vector field is irrotational.

Q37: If r = x i + y

Q38: Use Green's Theorem to evaluate the line

Q39: Evaluate the integral Evaluate the</p></div><svg width=

Q40: Use Green's Theorem to compute

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents