Solved

Solve the Initial-Value Problem = K × R with Initial

Question 25

Multiple Choice

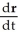Solve the initial-value problem Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve.


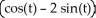A) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 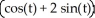i + Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3.
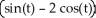B) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 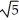i - Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 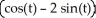j + 3 k,a circle with centre (0, 0, 3) and radius Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. in the plane z = 3.
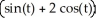C) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. 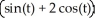i - Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3.
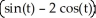D) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. i + Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. in the plane z = 3.
E) r(t) = Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. i + Solve the initial-value problem = k × r with initial condition r(0) = i + 2j + 3k. Describe the solution curve. A) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. B) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. C) r(t) = i - j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. D) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius in the plane z = 3. E) r(t) = i + j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3. j + 3 k,a circle with centre (0, 0, 3) and radius 5 in the plane z = 3.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q20: Assuming u(t) has continuous derivatives of all

Q21: If u and v are differentiable functions

Q22: If r(t) , v(t) and a(t) are

Q23: A particle moves around the elliptical cylinder

Q24: A ball of ice having mass 100

Q26: You are at the origin in the

Q27: A rocket is fired vertically in a

Q28: A rocket with mass 60,000 kilogram (kg),

Q29: Which of the following parametrize the

Q30: Find a parametrization of the ellipse

Unlock this Answer For Free Now!

View this answer and more for free by performing one of the following actions

qr-code

Scan the QR code to install the App and get 2 free unlocks

upload documents

Unlock quizzes for free by uploading documents