Find a polynomial f(x) of lowest possible degree such that the curve y = f(x) , 0 x 1, can be used to join the straight line segments y = 0, x 0, and y = 1, x 1, to form a curve along which a particle can travel at constant speed without experiencing discontinuous acceleration.
A) f(x) = 10  - 15
- 15 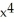 + 6
+ 6 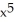
B) f(x) = 4 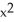 - 7
- 7 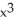 + 4
+ 4 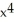
C) f(x) = 2  - 3
- 3 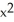 + 2
+ 2 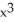
D) f(x) = 18 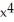 - 30
- 30 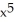 + 13
+ 13 
E) f(x) = 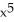 - 3
- 3  + 2
+ 2 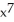
Correct Answer:
Verified
Q68: Find the radius of curvature of
Q69: The speed and the magnitude of the
Q70: Find the tangential and normal components of
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents