Essay
Let f(x) denote the sum of the series 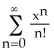 wherever the series converges. Where does the series converge? Calculate
wherever the series converges. Where does the series converge? Calculate  (x) and f(0). What do these results imply that f(x) actually is?
(x) and f(0). What do these results imply that f(x) actually is?
Correct Answer:
Verified
Series converges to ...
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Related Questions
Q82: Q83: Q84: The radius of convergence of the Q85: By suitably manipulating the geometric series Q86: Using the known geometric series representation Unlock this Answer For Free Now! View this answer and more for free by performing one of the following actions Scan the QR code to install the App and get 2 free unlocks Unlock quizzes for free by uploading documents![]()
![]()

