Suppose Newton's Method applied to f(x) =  is used to "find"the root of the equation
is used to "find"the root of the equation 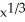 = 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
= 0 with initial guess x0 = r 0. What result does the first iteration of the method yield? The second iteration? The nth iteration? Why do these not converge to the obvious root x = 0 no matter how close the initial guess r was to that root?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q23: Newton's Method with the initial approximation x1
Q24: The function f(x) = ( 
Q25: Find all the roots of the equation
Q26: Give the iteration formula for finding the
Q27: Use Newton's Method to find the roots
Q29: By considering the locations of its critical
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents