Consider the initial value problem 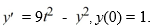 This question relates to using the Euler method to approximate the solution of this problem at t = 0.1 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.1 using a step size of h = 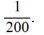 Which of the following equals
Which of the following equals 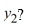
A)
B)
C)
D)
Correct Answer:
Verified
Q14: Given the initial value problem 
Q15: Given the initial value problem 
Q16: Consider the initial value problem 
Q17: Consider the initial value problem
Q18: Consider the initial value problem 
Q20: Consider the initial value problem
Q21: Consider the initial value problem
Q22: Consider the initial value problem 
Q23: Consider the initial value problem
Q24: Consider the initial value problem
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents