Multiple Choice
Into which of the following systems can this homogeneous third-order differential equation be transformed?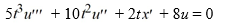
A)
B)
C)
D)
Correct Answer:
Verified
Related Questions
Q1: Into which of the following systems can
Q3: Transform this nonhomogeneous second-order initial value problem
Q4: Consider this system of first-order differential equations:
Q5: Consider this system of first-order differential
Q6: Compute: Q7: Compute: Q8: Consider these matrices: Q9: Consider the matrix Q10: If A is an 2 × 4 Q11: Consider these matrices: Unlock this Answer For Free Now! View this answer and more for free by performing one of the following actions Scan the QR code to install the App and get 2 free unlocks Unlock quizzes for free by uploading documents![]()
![]()
![]()
![]()
D = ![]()

