Consider the first-order nonhomogeneous initial value problem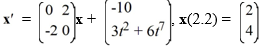
Given a fundamental matrix 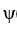 (t) for the system, what is the solution of this initial value problem?
(t) for the system, what is the solution of this initial value problem?
A)
B)
C)
D)
Correct Answer:
Verified
Q87: Consider the first-order nonhomogeneous initial value
Q88: Consider the first-order nonhomogeneous initial value problem
Q89: Consider the first-order nonhomogeneous initial value problem
Q90: Consider the first-order nonhomogeneous initial value problem
Q91: Consider the first-order nonhomogeneous initial value
Q92: Consider the first-order nonhomogeneous initial value
Q93: Consider the first-order nonhomogeneous initial value
Q95: Consider the first-order nonhomogeneous initial value
Q96: Consider the first-order nonhomogeneous initial value
Q97: Express the following third-order nonhomogeneous differential equation
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents