Solve the Problem $52 \mathrm{ft}$ And the Vertical Clearance Must Be $26 \mathrm{ft}$

Solve the problem.
-A railroad tunnel has the shape of half an ellipse. The height of the tunnel at the center is $52 \mathrm{ft}$ and the vertical clearance must be $26 \mathrm{ft}$ at a point $24 \mathrm{ft}$ from the center. Find an equation for the ellipse, where $\mathrm{x}$ and $\mathrm{y}$ are measured in 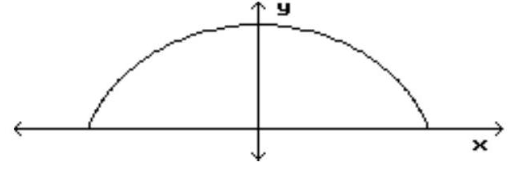$\mathrm{ft}$ .

A) $\frac{x^{2}}{768}+\frac{y^{2}}{676}=1$

B) $\frac{x^{2}}{576}+\frac{y^{2}}{2704}=1$

C) $\frac{x^{2}}{2704}+\frac{y^{2}}{768}=1$

D) $\frac{x^{2}}{768}+\frac{y^{2}}{2704}=1$