(See Problem 2.) Willy's only source of wealth is his chocolate factory. He has the utility function 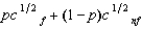, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = . The value of Willy's factory is $800,000 if there is no flood and 0 if there is a flood. 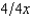Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company $ whether there is a flood or not, but he gets back $x from the company if there is a flood. Willy should buy A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there is a flood or not. B) no insurance since the cost per dollar of insurance exceeds the probability of a flood. C) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood. D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.. E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood

Question

Quizplus · Accepted Answer

Willy's expected utility function can be expressed as:
U(p) = p*ln(800,000 - x) + (1-p)*ln(800,000)
where x is the amount of insurance he buys.
To maximize his expected utility, Willy should choose x such that the marginal utility of wealth from buying insurance is equal to the marginal cost of buying insurance:
MU(800,000 - x)/[800,000 - x + p*x] = MC(x)
where MU is the marginal utility function and MC is the marginal cost function.
Taking the derivative of both sides with respect to x and setting it equal to 0, we get:
[p*(800,000 - x)]/[800,000 - x + p*x]^2 = 1/[2(800,000 - x)]
Solving for x, we get:
x = (200,000*p)/[1+p]
Substituting p = 0.01, we get x = $1,980.
Therefore, Willy should buy $1,980 worth of insurance so that if there is a flood, his wealth will be equal to 99% of what it would be if there is no flood.