(See Problem 11.) Albert's expected utility function is 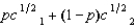 , where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Albert is offered a choice between getting a sure payment of $Z or a lottery in which he receives $400 with probability .30 or $2,500 with probability .70. Albert will choose the sure payment if
, where p is the probability that he consumes c1 and 1 - p is the probability that he consumes c2. Albert is offered a choice between getting a sure payment of $Z or a lottery in which he receives $400 with probability .30 or $2,500 with probability .70. Albert will choose the sure payment if
A) Z > 2,090.50 and the lottery if Z < 2,090.50.
B) Z > 1,040.50 and the lottery if Z < 1,040.50.
C) Z > 2,500 and the lottery if Z < 2,500.
D) Z > 1,681 and the lottery if Z < 1,681.
E) Z > 1,870 and the lottery if Z < 1,870.
Correct Answer:
Verified
Q4: (See Problem 11.) Pete's expected utility function
Q5: In Problem 9, Billy has a von
Q6: In Problem 9, Billy has a von
Q7: (See Problem 11.) Lawrence's expected utility function
Q8: Sally Kink is an expected utility maximizer
Q10: Sally Kink is an expected utility maximizer
Q11: (See Problem 2.) Willy's only source of
Q12: In Problem 9, Billy has a von
Q13: (See Problem 11.) Wilfred's expected utility function
Q14: Sally Kink is an expected utility maximizer
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents