Multiple Choice
If f(x) = 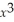 + 3
+ 3 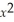
- 24x + 8,then f is
A) decreasing on (-∞, 4) , concave up on (-1, ∞) , and has no relative minimum point.
B) decreasing on (1, 2) , concave up (0, ∞) , and has a relative minimum when x = -4.
C) increasing on (2, ∞) , concave up on (-∞, -1) , and has a relative minimum when x = 2.
D) increasing on (-4, 2) , concave down on (-∞, ∞) , and has a relative maximum when x = 2.
E) decreasing on (-4, 2) , concave down on (-∞, -1) , and has a relative maximum when x = -4.
Correct Answer:
Verified
Related Questions


