A brokerage house offers three stock portfolios. Portfolio I consists of 2 blocks of common stock and 1 municipal bond. Portfolio II consists of 4 blocks of common stock, 2 municipal bonds, and 3 blocks of preferred stock. Portfolio III consists of 2 blocks of common stock, 1 municipal bond, and 3 blocks of preferred stock. A customer wants 16 blocks of common stock, 8 municipal bonds, and 6 blocks of preferred stock. Let x equal the number of units of Portfolio I, y equal the number of units of Portfolio II, and z equal the number of units of Portolio III. If the numbers of the three portfolios offered must be integers, find the general solution that can be used to determine all possible offerings.
A) 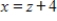 ,
, 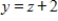 ,
, 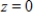
B) 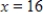 ,
, 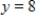 ,
, 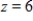
C) 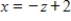 ,
, 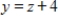 ,
, 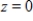
D) 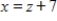 ,
, 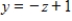 ,
, 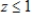
E) 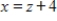 ,
, 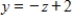 ,
, 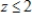
Correct Answer:
Verified
Q130: A trust account manager has $220,000 to
Q137: Use technology to solve the system of
Q138: A system of equations may have a
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents