Use the following steps.
A) Write an equation for the areas using integrals.
B) Differentiate the equation in A and solve the resulting linear equation.
Ans:
A) 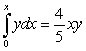 B)
B) 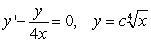
-A pool contains 12 million gal of fresh water. Contaminated water flows into the pool at a rate of 4 million gal/year as the mixture in the pool flows out at the same rate.
The concentration 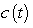 of the chemical in the incoming contaminated water is
of the chemical in the incoming contaminated water is  g/gal, where t is in years.
g/gal, where t is in years.
Find the amount 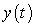 of the chemical in the pool at time
of the chemical in the pool at time 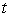 .
.
Correct Answer:
Verified
Q63: Solve the differential equation Q64: Solve the following equations. Q65: The differential equation Q66: The differential equation Q67: The differential equation Q68: Solve the initial value problem Q69: Solve the initial value problem Q71: The curves orthogonal to the solutions of Q72: Solve the differential equation Q73: Solve the initial value problem Unlock this Answer For Free Now! View this answer and more for free by performing one of the following actions Scan the QR code to install the App and get 2 free unlocks Unlock quizzes for free by uploading documents![]()
A) ![]()
![]()
![]()
![]()


![]()


