Find the mass of the solid whose base is the region inside the unit circle  , and the cross sections parallel to the x-axis and perpendicular to the base are semicircles whose diameters are on the base.
, and the cross sections parallel to the x-axis and perpendicular to the base are semicircles whose diameters are on the base.
The density function is 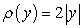 .
. 
Correct Answer:
Verified
Q17: Find the area of the region bounded
Q18: Find the area of the shaded region
Q19: Find the volume of the solid whose
Q20: Find the area of the region bounded
Q21: Compute the volume of the solid whose
Q23: Calculate the population within a 2-mile radius
Q24: Find the volume of the solid obtained
Q25: Calculate the population within a 2-mile radius
Q26: A solid circular cylinder of radius
Q27: Compute the volume of the solid whose
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents