Find the critical point(s) of the function. Then use the second derivative test to classify the nature of each point, if possible. Finally, determine the relative extrema of the function. 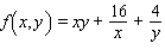
A) (4, 1) is the critical point, the function has neither a relative maximum nor a relative minimum at this point
B) (4, 1) is the critical point, it is impossible to determine the relative extrema of the function
C) (4, 1) is the point of maximum, 12 is the relative maximum
D) (4, 1) is the point of minimum, 12 is the relative minimum
E) no critical points
Correct Answer:
Verified
Q131: Find the critical point(s) of the function.
Q132: Find the critical point(s) of the function.
Q133: Find the critical point(s) of the function.
Q134: Find the critical point(s) of the function.
Q135: Find the critical point(s) of the function.
Q137: An auxiliary electric power station will serve
Q138: An open rectangular box having a volume
Q139: Find the critical point(s) of the function.
Q140: Find the critical point(s) of the function.
Q141: Determine whether the statement is true or
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents