A cylindrical container for storing radioactive waste is to be constructed from lead and have a thickness of 6 in. (see the figure) . If the volume of the outside cylinder is to be 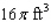 , find the radius and the height of the inside cylinder that will result in a container of maximum storage capacity.
, find the radius and the height of the inside cylinder that will result in a container of maximum storage capacity.  Hint: Show that the storage capacity (inside volume) is given by
Hint: Show that the storage capacity (inside volume) is given by 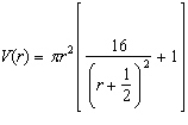
A) r = 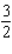 ft.; h = 2 ft.
ft.; h = 2 ft.
B) r = 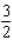 ft.; h = 3 ft.
ft.; h = 3 ft.
C) r = 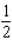 ft.; h = 2 ft.
ft.; h = 2 ft.
D) r = 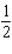 ft.; h = 3 ft.
ft.; h = 3 ft.
Correct Answer:
Verified
Q13: A Norman window has the shape of
Q14: What are the dimensions of a closed
Q15: A wooden beam has a rectangular cross
Q16: A book designer has decided that the
Q17: If an open box has a square
Q19: A rectangular box is to have a
Q20: The management of the UNICO department store
Q21: You are given the graph of some
Q22: A rectangular box is to have a
Q23: A book designer has decided that the
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents