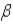If _j, an unbiased estimator of _j, is consistent, then the: A)distribution of _j becomes more and more loosely distributed around _j as the sample size grows. B)distribution of _j becomes more and more tightly distributed around 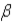_j as the sample size grows. C) distribution of _j tends toward a standard normal distribution as the sample size grows. D) distribution of _j remains unaffected as the sample size grows.

Question

Quizplus · Accepted Answer

Consistency means that as the sample size grows, the estimator converges in probability to the true value of the parameter being estimated. In other words, the distribution of the estimator becomes more and more tightly distributed around the true value as the sample size grows. Therefore, option B is the correct choice. Option A suggests that the distribution becomes more loosely distributed, which contradicts the idea of consistency. Option C suggests that the distribution converges to a standard normal distribution, which is not necessarily true for all estimators. Option D suggests that the distribution remains unaffected, which is also not consistent with consistency. If 11eab06d_2506_fc4b_beed_5d64120d97da_TB2133_11 _j, an unbiased estimator of 11eab06d_2506_fc4c_beed_ebf1c189f882_TB2133_11 _j, is consistent, then the distribution of 11eab06d_2506_fc4d_beed_ad9beb110086_TB2133_11 _j becomes more and more tightly distributed around 11eab06d_2507_235e_beed_6ddd714edcfc_TB2133_11 _j as the sample size grows.

If j, an Unbiased Estimator of j, Is

If _j, an Unbiased Estimator of _j, Is