Your textbook uses the following example of simultaneous causality bias of a two equation system:
Yi = β0 + β1Xi + ui
Xi = 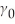 +
+ 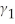 Yi + vi
Yi + vi
To be more specific,think of the first equation as a demand equation for a certain good,where Y is the quantity demanded and X is the price.The second equation then represents the supply equation,with a third equation establishing that demand equals supply.Sketch the market outcome over a few periods and explain why it is impossible to identify the demand and supply curves in such a situation.Next assume that an additional variable enters the demand equation: income.In a new graph,draw the initial position of the demand and supply curves and label them D0 and S0.Now allow for income to take on four different values and sketch what happens to the two curves.Is there a pattern that you see which suggests that you might be able to identify one of the two equations with real-life data?
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q40: One of the most frequently used summary
Q41: Your professor wants to measure the class's
Q42: Assume that you had found correlation of
Q43: Assume that a simple economy could be
Q44: Your textbook states that correlation of the
Q46: Explain why the OLS estimator for the
Q48: Your textbook has analyzed simultaneous equation systems
Q49: Give at least three examples where you
Q53: A professor in your microeconomics lectures derived
Q59: Think of three different economic examples where
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents