Let p be the success probability of a Bernoulli random variable Y,i.e. ,p = Pr(Y = 1).It can be shown that 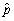 ,the fraction of successes in a sample,is asymptotically distributed N(p,
,the fraction of successes in a sample,is asymptotically distributed N(p, 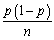 .Using the estimator of the variance of
.Using the estimator of the variance of 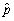 ,
, 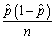 ,construct a 95% confidence interval for p.Show that the margin for sampling error simplifies to 1/
,construct a 95% confidence interval for p.Show that the margin for sampling error simplifies to 1/ 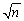 if you used 2 instead of 1.96 assuming,conservatively,that the standard error is at its maximum.Construct a table indicating the sample size needed to generate a margin of sampling error of 1%,2%,5% and 10%.What do you notice about the increase in sample size needed to halve the margin of error? (The margin of sampling error is 1.96×SE(
if you used 2 instead of 1.96 assuming,conservatively,that the standard error is at its maximum.Construct a table indicating the sample size needed to generate a margin of sampling error of 1%,2%,5% and 10%.What do you notice about the increase in sample size needed to halve the margin of error? (The margin of sampling error is 1.96×SE( 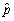 ))
))
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q41: Your textbook states that when you test
Q42: At the Stock and Watson (http://www.pearsonhighered.com/stock_watson)website go
Q42: During the last few days before a
Q44: Let Y be a Bernoulli random variable
Q48: The development office and the registrar have
Q48: A manufacturer claims that a certain brand
Q49: Imagine that you had sampled 1,000,000 females
Q50: Some policy advisors have argued that education
Q53: The accompanying table lists the height
Q61: Consider two estimators: one which is biased
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents