Suppose a Simple Random Sample Is Selected from a Population $\mu$

Suppose a simple random sample is selected from a population with a mean if $\mu$ and a variance of $\sigma$ ².The central limit theorem tells us that

A) the sample mean 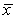gets closer to the population mean $\mu$ as the sample size increases.
B) if the sample size n is sufficiently large,the sample will be approximately Normal.
C) the mean of 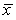will be $\mu$ if the sample size n is sufficiently large.
D) if the sample size is sufficiently large,the distribution of 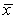will be approximately Normal with a mean of $\mu$ and a standard deviation of
.
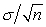E) the distribution of 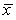will be Normal only if the population from which the sample is selected is also Normal.