Bayer Pharmaceutical produces three kinds of cold formulas: formula I, formula II, and formula III. It takes 2.5 hr to produce 1,000 bottles of formula I, 3 hr to produce 1,000 bottles of formula II, and 4 hr to produce 1,000 bottles of formula III. The profits for each 1,000 bottles of formula I, formula II, and formula III are $180, $200, and $300, respectively. For a certain production run, there are enough ingredients on hand to make at most 8,000 bottles of formula I, 15,000 bottles of formula II, and 7,000 bottles of formula III. Furthermore, the time for the production run is limited to a maximum of 65 hr. How many bottles of each formula should be produced in this production run so that the profit is maximized?
A) Minimize P = 180x + 200y + 300z subject to 
B) Minimize P = 180x + 200y + 300z subject to 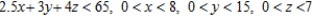
C) Minimize P = 180x + 200y + 300z subject to 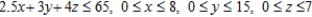
D) Maximize P = 180x + 200y + 300z subject to 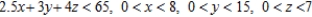
E) Maximize P = 180x + 200y + 300z subject to 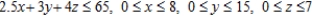
Correct Answer:
Verified
Q126: Find the optimal (maximum and/or minimum) value(s)
Q127: Ace Novelty manufactures Gaint Pandas and Saint
Q128: A division of the Winston Furniture Company
Q129: Patricia has at most $36,000 to invest
Q130: A hunger-relief organization has earmarked between $2
Q132: A division of the Winston Furniture Company
Q133: Perth Mining Company operates two mines for
Q134: As a part of a campaign to
Q135: Solve the linear programming problem by the
Q136: A corporation has a division that produces
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents