Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 2 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $2, and the profit for each model B grate is $1.50. 1,000 lb of cast iron and 20 labor-hours are available for the production of grates each day. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 200 grates per day. How many grates of each model should the division produce daily to maximize Kane's profits?
Use the method of corners to solve the problem. Find the range of values that the coefficient of x can assume without changing the optimal solution. Identify the binding and nonbinding constraints.
A) Produce 100 grates of model A, 100 grates of model B; maximum profit of $504; Range: 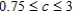 ; Constraints 2 and 3 are binding; constraint 1 is not.
; Constraints 2 and 3 are binding; constraint 1 is not.
B) Produce 200 grates of model A, 100 grates of model B; maximum profit of $500; Range: 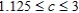 ; Constraints 1 and 2 are binding; constraint 3 is not.
; Constraints 1 and 2 are binding; constraint 3 is not.
C) Produce 100 grates of model A, 200 grates of model B; maximum profit of $500; Range: 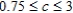 ; Constraints 1 and 2 are binding; constraint 3 is not.
; Constraints 1 and 2 are binding; constraint 3 is not.
Correct Answer:
Verified
Q189: Soundex produces two models of clock radios.
Q190: Perth Mining Company operates two mines for
Q191: You are given a linear programming problem.
Q192: Consider the production problem: One company wishes
Q193: Use the method of corners to solve
Q195: Soundex produces two models of clock radios.
Q196: A farmer plans to plant two crops,
Q197: A company manufactures two products, A and
Q198: Ace Novelty wishes to produce two types
Q199: Soundex produces two models of clock radios.
Unlock this Answer For Free Now!
View this answer and more for free by performing one of the following actions

Scan the QR code to install the App and get 2 free unlocks

Unlock quizzes for free by uploading documents