
Basic Econometrics 5th Edition by Damodar Gujarati,Dawn Porter
النسخة 5الرقم المعياري الدولي: 978-0073375779
Basic Econometrics 5th Edition by Damodar Gujarati,Dawn Porter
النسخة 5الرقم المعياري الدولي: 978-0073375779 تمرين 1
"If two random variables are statistically independent, the coefficient of correlation between the two is zero. But the converse is not necessarily true; that is, zero correlation does not imply statistical independence. However, if two variables are normally distributed, zero correlation necessarily implies statistical independence." Verify this statement for the following joint probability density function of two normally distributed variables Y 1 and Y 2 (this joint probability density function is known as the bivariate normal probability density function): 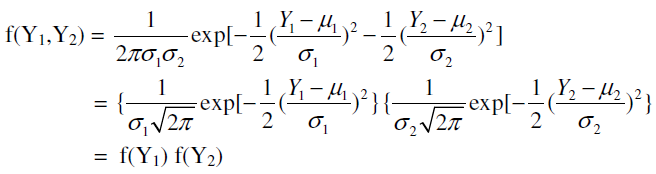
4 See Appendix A for a general discussion of the properties of the maximum likelihood estimators as well as for the distinction between asymptotic unbiasedness and consistency. Roughly speaking, in asymptotic unbiasedness we try to find out the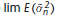 as n tends to infinity, where n is the sample size on which the estimator is based, whereas in consistency we try to find out how
as n tends to infinity, where n is the sample size on which the estimator is based, whereas in consistency we try to find out how 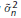 behaves as n increases indefinitely. Notice that the unbiasedness property is a repeated sampling property of an estimator based on a sample of given size, whereas in consistency we are concerned with the behavior of an estimator as the sample size increases indefinitely.
behaves as n increases indefinitely. Notice that the unbiasedness property is a repeated sampling property of an estimator based on a sample of given size, whereas in consistency we are concerned with the behavior of an estimator as the sample size increases indefinitely.
where µ 1 = mean of Y 1
µ 2 = mean of Y 2
1 = standard deviation of Y 1
2 = standard deviation of Y 2
= coefficient of correlation between Y 1 and Y 2
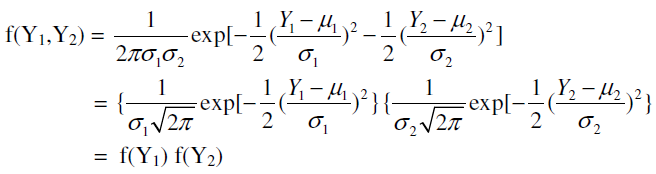
4 See Appendix A for a general discussion of the properties of the maximum likelihood estimators as well as for the distinction between asymptotic unbiasedness and consistency. Roughly speaking, in asymptotic unbiasedness we try to find out the
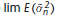 as n tends to infinity, where n is the sample size on which the estimator is based, whereas in consistency we try to find out how
as n tends to infinity, where n is the sample size on which the estimator is based, whereas in consistency we try to find out how 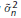 behaves as n increases indefinitely. Notice that the unbiasedness property is a repeated sampling property of an estimator based on a sample of given size, whereas in consistency we are concerned with the behavior of an estimator as the sample size increases indefinitely.
behaves as n increases indefinitely. Notice that the unbiasedness property is a repeated sampling property of an estimator based on a sample of given size, whereas in consistency we are concerned with the behavior of an estimator as the sample size increases indefinitely.where µ 1 = mean of Y 1
µ 2 = mean of Y 2
1 = standard deviation of Y 1
2 = standard deviation of Y 2
= coefficient of correlation between Y 1 and Y 2
التوضيح
The objective of the following analysis ...
Basic Econometrics 5th Edition by Damodar Gujarati,Dawn Porter
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








