
Introduction to Econometrics 3rd Edition by James Stock, James Stock
النسخة 3الرقم المعياري الدولي: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, James Stock
النسخة 3الرقم المعياري الدولي: 978-9352863501 تمرين 2
This exercise fills in the details of the derivation of the asymptotic distribution of 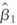 given in Appendix 4.3.
given in Appendix 4.3.
a. Use Equation (17.19) to derive the expression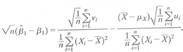
where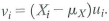
b. Use the central limit theorem, the law of large numbers, and Slutsky s theorem to show that the final term in the equation converges in probability to zero.
c. Use the Cauchy-Schwarz inequality and the third least squaies assumption in Key Concept 17.1 to prove that var( v i ) . Does the term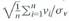 satisfy the central limit theorem
satisfy the central limit theorem
d. Apply the central limit theorem and Slutsky's theorem to obtain the result in Equation (17.12).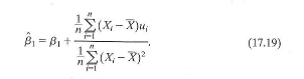

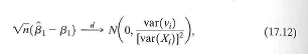
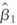 given in Appendix 4.3.
given in Appendix 4.3.a. Use Equation (17.19) to derive the expression
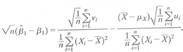
where
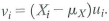
b. Use the central limit theorem, the law of large numbers, and Slutsky s theorem to show that the final term in the equation converges in probability to zero.
c. Use the Cauchy-Schwarz inequality and the third least squaies assumption in Key Concept 17.1 to prove that var( v i ) . Does the term
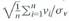 satisfy the central limit theorem
satisfy the central limit theorem d. Apply the central limit theorem and Slutsky's theorem to obtain the result in Equation (17.12).
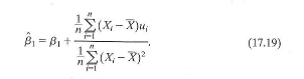

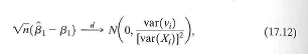
التوضيح
a) The given equation is Multiply by th...
Introduction to Econometrics 3rd Edition by James Stock, James Stock
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








