
Introduction to Econometrics 3rd Edition by James Stock, James Stock
النسخة 3الرقم المعياري الدولي: 978-9352863501
Introduction to Econometrics 3rd Edition by James Stock, James Stock
النسخة 3الرقم المعياري الدولي: 978-9352863501 تمرين 22
Consider the problem of minimizing the sum of squared residuals subject to the constraint that Rb = r, where R is q × ( k + 1) with rank cj. Let 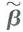 be the value of b that solves the constrained minimization problem.
be the value of b that solves the constrained minimization problem.
a. Show that the Lagrangian for the minimization problem is L(b , ) = ( Y- Xb ) ' ( Y-Xb ) + ' ( Rb - r ), where is a q × 1 vector of Lagrange multipliers.
b. Show that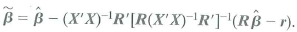
c. Show that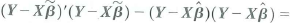

d. Show that F in Equation (18.36) is equivalent to the homoskeskasticity-only F -statistic in Equation (7.13).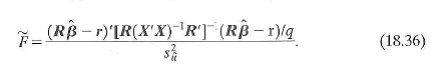

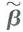 be the value of b that solves the constrained minimization problem.
be the value of b that solves the constrained minimization problem.a. Show that the Lagrangian for the minimization problem is L(b , ) = ( Y- Xb ) ' ( Y-Xb ) + ' ( Rb - r ), where is a q × 1 vector of Lagrange multipliers.
b. Show that
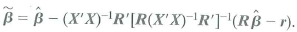
c. Show that
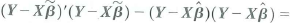

d. Show that F in Equation (18.36) is equivalent to the homoskeskasticity-only F -statistic in Equation (7.13).

التوضيح
a) The minimization is However it is co...
Introduction to Econometrics 3rd Edition by James Stock, James Stock
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








