
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609 تمرين 7
Let Y denote a Bernoulli( ) random variable with 0 1. Suppose we are interested in estimating the odds ratio, = /(1- ), which is the probability of success over the the probability of failure. Given a random sample {Y 1 , …, Y n }, we know that an unbiased and consistent estimator of is 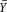 , the proportion of successes in n trials. A natural estimator of is G =
, the proportion of successes in n trials. A natural estimator of is G = 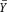 /(1 -
/(1 - 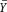 ), the proportion of successes over the proportion of failures in the sample.
), the proportion of successes over the proportion of failures in the sample.
(i) Why is G not an unbiased estimator of
(ii) Use PLIM.2(iii)
PLIM.2 If plim ( T n ) = and plim ( U n ) = , then
(i) plim( T n _+ U n ) = + ;
(ii) plim( T n U n ) = ;
(iii) plim( T n / U n ) = / , provided 0.
to show that G is a consistent estimator of .
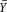 , the proportion of successes in n trials. A natural estimator of is G =
, the proportion of successes in n trials. A natural estimator of is G = 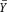 /(1 -
/(1 - 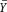 ), the proportion of successes over the proportion of failures in the sample.
), the proportion of successes over the proportion of failures in the sample.(i) Why is G not an unbiased estimator of
(ii) Use PLIM.2(iii)
PLIM.2 If plim ( T n ) = and plim ( U n ) = , then
(i) plim( T n _+ U n ) = + ;
(ii) plim( T n U n ) = ;
(iii) plim( T n / U n ) = / , provided 0.
to show that G is a consistent estimator of .
التوضيح
It is given that a natural estimator of ...
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








