
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609 تمرين 7
Several statistics are commonly used to detect nonnormality in underlying population distributions. Here we will study one that measures the amount of skewness in a distribution. Recall that any normally distributed random variable is symmetric about its mean; therefore, if we standardize a symmetrically distributed random variable, say z =(y =µ y )/ y , where µ y =E(y) and y = sd(y), then z has mean zero, variance one, and E(z 3 )= 0. Given a sample of data {y i : i _ 1,..., n}, we can standardize y i in the sample by using 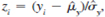 , where
, where 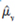 is the sample mean and
is the sample mean and 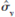 is the sample standard deviation. (We ignore the fact that these are estimates based on the sample.) A sample statistic that measures skewness is
is the sample standard deviation. (We ignore the fact that these are estimates based on the sample.) A sample statistic that measures skewness is 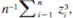 3, or where n is replaced with (n - t. If y has a normal distribution in the population, the skewness measure in the sample for the standardized values should not differ significantly from zero.
3, or where n is replaced with (n - t. If y has a normal distribution in the population, the skewness measure in the sample for the standardized values should not differ significantly from zero.
(i) First use the data set 401KSUBS.RAW, keeping only observations with fsize = 1. Find the skewness measure for inc. Do the same for log(inc). Which variable has more skewness and therefore seems less likely to be normally distributed
(ii) Next use BWGHT2.RAW. Find the skewness measures for bwght and log(bwght). What do you conclude
(iii) Evaluate the following statement: "The logarithmic transformation always makes a positive variable look more normally istributed."
(iv) If we are interested in the normality assumption in the context of regression, should we be evaluating the unconditional distributions of y and log(y) Explain.
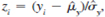 , where
, where 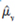 is the sample mean and
is the sample mean and 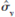 is the sample standard deviation. (We ignore the fact that these are estimates based on the sample.) A sample statistic that measures skewness is
is the sample standard deviation. (We ignore the fact that these are estimates based on the sample.) A sample statistic that measures skewness is 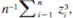 3, or where n is replaced with (n - t. If y has a normal distribution in the population, the skewness measure in the sample for the standardized values should not differ significantly from zero.
3, or where n is replaced with (n - t. If y has a normal distribution in the population, the skewness measure in the sample for the standardized values should not differ significantly from zero.(i) First use the data set 401KSUBS.RAW, keeping only observations with fsize = 1. Find the skewness measure for inc. Do the same for log(inc). Which variable has more skewness and therefore seems less likely to be normally distributed
(ii) Next use BWGHT2.RAW. Find the skewness measures for bwght and log(bwght). What do you conclude
(iii) Evaluate the following statement: "The logarithmic transformation always makes a positive variable look more normally istributed."
(iv) If we are interested in the normality assumption in the context of regression, should we be evaluating the unconditional distributions of y and log(y) Explain.
التوضيح

هذا السؤال ليس له إجابة موثقة من أحد الخبراء بعد، دع الذكاء الاصطناعي Copilot في كويز بلس يساعدك في إيجاد الحل.
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








