
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609 تمرين 11
Use the data in 401KSUBS.RAW for this exercise.
(i) Compute the average, standard deviation, minimum, and maximum values of nettfa in the sample.
(ii) Test the hypothesis that average nettfa does not differ by 401(k) eligibility status; use a two-sided alternative. What is the dollar amount of the estimated difference
(iii) From part (ii) of Computer Exercise, it is clear that e401k is not exogenous in a simple regression model; at a minimum, it changes by income and age. Estimate a multiple linear regression model for nettfa that includes income, age, and e401k as explanatory variables. The income and age variables should appear as quadratics. Now, what is the estimated dollar effect of 401(k) eligibility
(iv) To the model estimated in part (iii), add the interactions e401k • (age _ 41) and e401k • (age _ 41) 2. Note that the average age in the sample is about 41, so that in the new model, the coefficient on e401k is the estimated effect of 401(k) eligibilityat the average age. Which interaction term is significant
(v) Comparing the estimates from parts (iii) and (iv), do the estimated effects of 401(k) eligibility at age 41 differ much Explain.
(vi) Now, drop the interaction terms from the model, but define five family size dummy variables: fsize1, fsize2, fsize3, fsize4, and fsize5. The variable fsize5 is unity for families with five or more members. Include the family size dummies in the model estimated from part (iii); be sure to choose a base group. Are the family dummies significant at the 1% level
(vii) Now, do a Chow test for the model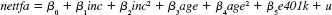
across the five family size categories, allowing for intercept differences. The restricted sum of squared residuals, SSR r , is obtained from part (vi) because that regression assumes all slopes are the same. The unrestricted sum of squared residuals is SSR ur = SSR 1 = SSR 2 =... = SSR 5 , where SSR f is the sum of squared residuals for the equation estimated using only family size f. You should convince yourself that there are 30 parameters in the unrestricted model (5 intercepts plus 25 slopes) and 10 parameters in the restricted model (5 intercepts plus 5 slopes). Therefore, the number of restrictions being tested is q = 20, and the df for the unrestricted model is 9,275 _ 30 = 9,245.
Exercise There has been much interest in whether the presence of 401(k) pension plans, available to many U.S. workers, increases net savings. The data set 401KSUBS.RAW contains information on net financial assets (nettfa), family income (inc), a binary variable for eligibility in a 401(k) plan (e401k), and several other variables.
(i) What fraction of the families in the sample are eligible for participation in a 401(k) plan
(ii) Estimate a linear probability model explaining 401(k) eligibility in terms of income, age, and gender. Include income and age in quadratic form, and report the results in the usual form.
(iii) Would you say that 401(k) eligibility is independent of income and age What about gender Explain.
(iv) Obtain the fitted values from the linear probability model estimated in part (ii). Are any fitted values negative or greater than one
(v) Using the fitted values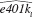 from part (iv), define
from part (iv), define  and
and 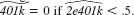 Out of 9,275 families, how many are predicted to be eligible for a 401(k) plan
Out of 9,275 families, how many are predicted to be eligible for a 401(k) plan
(vi) For the 5,638 families not eligible for a 401(k), what percentage of these are predicted not to have a 401(k), using the predictor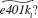 For the 3,637 families eligible for a 401(k) plan, what percentage are predicted to have one (It is helpful if your econometrics package has a "tabulate" command.)
For the 3,637 families eligible for a 401(k) plan, what percentage are predicted to have one (It is helpful if your econometrics package has a "tabulate" command.)
(vii) The overall percent correctly predicted is about 64.9%. Do you think this is a complete description of how well the model does, given your answers in part (vi)
(viii) Add the variable pira as an explanatory variable to the linear probability model. Other things equal, if a family has someone with an individual retirement account, how much higher is the estimated probability that the family is eligible for a 401(k) plan Is it statistically different from zero at the 10% level
(i) Compute the average, standard deviation, minimum, and maximum values of nettfa in the sample.
(ii) Test the hypothesis that average nettfa does not differ by 401(k) eligibility status; use a two-sided alternative. What is the dollar amount of the estimated difference
(iii) From part (ii) of Computer Exercise, it is clear that e401k is not exogenous in a simple regression model; at a minimum, it changes by income and age. Estimate a multiple linear regression model for nettfa that includes income, age, and e401k as explanatory variables. The income and age variables should appear as quadratics. Now, what is the estimated dollar effect of 401(k) eligibility
(iv) To the model estimated in part (iii), add the interactions e401k • (age _ 41) and e401k • (age _ 41) 2. Note that the average age in the sample is about 41, so that in the new model, the coefficient on e401k is the estimated effect of 401(k) eligibilityat the average age. Which interaction term is significant
(v) Comparing the estimates from parts (iii) and (iv), do the estimated effects of 401(k) eligibility at age 41 differ much Explain.
(vi) Now, drop the interaction terms from the model, but define five family size dummy variables: fsize1, fsize2, fsize3, fsize4, and fsize5. The variable fsize5 is unity for families with five or more members. Include the family size dummies in the model estimated from part (iii); be sure to choose a base group. Are the family dummies significant at the 1% level
(vii) Now, do a Chow test for the model
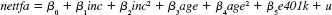
across the five family size categories, allowing for intercept differences. The restricted sum of squared residuals, SSR r , is obtained from part (vi) because that regression assumes all slopes are the same. The unrestricted sum of squared residuals is SSR ur = SSR 1 = SSR 2 =... = SSR 5 , where SSR f is the sum of squared residuals for the equation estimated using only family size f. You should convince yourself that there are 30 parameters in the unrestricted model (5 intercepts plus 25 slopes) and 10 parameters in the restricted model (5 intercepts plus 5 slopes). Therefore, the number of restrictions being tested is q = 20, and the df for the unrestricted model is 9,275 _ 30 = 9,245.
Exercise There has been much interest in whether the presence of 401(k) pension plans, available to many U.S. workers, increases net savings. The data set 401KSUBS.RAW contains information on net financial assets (nettfa), family income (inc), a binary variable for eligibility in a 401(k) plan (e401k), and several other variables.
(i) What fraction of the families in the sample are eligible for participation in a 401(k) plan
(ii) Estimate a linear probability model explaining 401(k) eligibility in terms of income, age, and gender. Include income and age in quadratic form, and report the results in the usual form.
(iii) Would you say that 401(k) eligibility is independent of income and age What about gender Explain.
(iv) Obtain the fitted values from the linear probability model estimated in part (ii). Are any fitted values negative or greater than one
(v) Using the fitted values
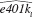 from part (iv), define
from part (iv), define  and
and 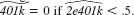 Out of 9,275 families, how many are predicted to be eligible for a 401(k) plan
Out of 9,275 families, how many are predicted to be eligible for a 401(k) plan (vi) For the 5,638 families not eligible for a 401(k), what percentage of these are predicted not to have a 401(k), using the predictor
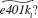 For the 3,637 families eligible for a 401(k) plan, what percentage are predicted to have one (It is helpful if your econometrics package has a "tabulate" command.)
For the 3,637 families eligible for a 401(k) plan, what percentage are predicted to have one (It is helpful if your econometrics package has a "tabulate" command.)(vii) The overall percent correctly predicted is about 64.9%. Do you think this is a complete description of how well the model does, given your answers in part (vi)
(viii) Add the variable pira as an explanatory variable to the linear probability model. Other things equal, if a family has someone with an individual retirement account, how much higher is the estimated probability that the family is eligible for a 401(k) plan Is it statistically different from zero at the 10% level
التوضيح

هذا السؤال ليس له إجابة موثقة من أحد الخبراء بعد، دع الذكاء الاصطناعي Copilot في كويز بلس يساعدك في إيجاد الحل.
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








