
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
النسخة 4الرقم المعياري الدولي: 978-0324660609 تمرين 13
Use the data set in BEAUTY.RAW, which contains a subset of the variables (but more usable observations than in the regressions) reported by Hamermesh and Biddle (1994).
(i) Find the separate fractions of men and women that are classified as having above average looks. Are more people rated as having above average or below average looks
(ii) Test the null hypothesis that the population fractions of above-average-looking women and men are the same. Report the one-sided p -value that the fraction is higher for women. ( Hint: Estimating a simple linear probability model is easiest.)
(iii) Now estimate the model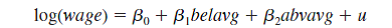
separately for men and women, and report the results in the usual form. In both cases, interpret the coefficient on belavg. Explain in words what the hypothesis H 0 :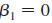 against H 1 :
against H 1 :  means, and find the p -values for men and women.
means, and find the p -values for men and women.
(iv) Is there convincing evidence that women with above average looks earn more than women with average looks Explain.
(v) For both men and women, add the explanatory variables educ , exper , exper 2 , union , goodhlth , black , married , south , bigcity , smllcity , and service. Do the effects of the "looks" variables change in important ways
(vi) Use the SSR form of the Chow F statistic to test whether the slopes of the regression functions in part (v) differ across men and women. Be sure to allow for an intercept shift under the null.
(i) Find the separate fractions of men and women that are classified as having above average looks. Are more people rated as having above average or below average looks
(ii) Test the null hypothesis that the population fractions of above-average-looking women and men are the same. Report the one-sided p -value that the fraction is higher for women. ( Hint: Estimating a simple linear probability model is easiest.)
(iii) Now estimate the model
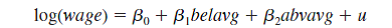
separately for men and women, and report the results in the usual form. In both cases, interpret the coefficient on belavg. Explain in words what the hypothesis H 0 :
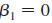 against H 1 :
against H 1 :  means, and find the p -values for men and women.
means, and find the p -values for men and women.(iv) Is there convincing evidence that women with above average looks earn more than women with average looks Explain.
(v) For both men and women, add the explanatory variables educ , exper , exper 2 , union , goodhlth , black , married , south , bigcity , smllcity , and service. Do the effects of the "looks" variables change in important ways
(vi) Use the SSR form of the Chow F statistic to test whether the slopes of the regression functions in part (v) differ across men and women. Be sure to allow for an intercept shift under the null.
التوضيح
Consider the provided data set "BEAUTY" ...
Introductory Econometrics 4th Edition by Jeffrey Wooldridge
لماذا لم يعجبك هذا التمرين؟
أخرى 8 أحرف كحد أدنى و 255 حرفاً كحد أقصى
حرف 255








