Deck 17: Behavioral Economics and Risk Taking
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/95
Play
Full screen (f)
Deck 17: Behavioral Economics and Risk Taking
1
The hypothetical species Homo economicus is acutely aware of opportunities in the environment and:
A)strives to maximize the benefits received from each course of action while minimizing the costs.
B)strives to minimize the benefits received from each course of action while maximizing the costs.
C)strives to equalize the benefits received and costs incurred from each course of action.
D)takes an action only if the benefits to society of this action outweigh the costs to society of this action.
E)never takes action because of the understanding that all individual actions are to the detriment of society.
A)strives to maximize the benefits received from each course of action while minimizing the costs.
B)strives to minimize the benefits received from each course of action while maximizing the costs.
C)strives to equalize the benefits received and costs incurred from each course of action.
D)takes an action only if the benefits to society of this action outweigh the costs to society of this action.
E)never takes action because of the understanding that all individual actions are to the detriment of society.
A
2
Most economic theory proceeds as though economic actors are all rational,self-interested decision-makers.Economists refer to this hypothetical rational,self-interested decision-maker as:
A)Homo consumus.
B)Homo microcus.
C)Homo demandcurvius.
D)Homo economicus.
E)Homo elasticious.
A)Homo consumus.
B)Homo microcus.
C)Homo demandcurvius.
D)Homo economicus.
E)Homo elasticious.
D
3
Behavioral economics studies how __________ influences the decision-making process.
A)the weather pattern
B)rational economic action
C)human psychology
D)the financial sector
E)macroeconomics
A)the weather pattern
B)rational economic action
C)human psychology
D)the financial sector
E)macroeconomics
C
4
A relatively new area in the field of economics called __________ studies people who appear to make choices that do not seem rational in an economic sense.
A)business-cycle economics
B)financial economics
C)behavioral economics
D)labor economics
E)entrepreneurial economics
A)business-cycle economics
B)financial economics
C)behavioral economics
D)labor economics
E)entrepreneurial economics

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
5
For mathematical convenience,assuming that people are fully rational and self-interested:
A)clearly does not mean that people really are fully rational and self-interested all the time.
B)clearly means that people really are fully rational and self-interested all the time.
C)is a practice never followed by economists but is often followed by psychologists.
D)is a practice always followed by behavioral economists.
E)is a practice that is banned in most states by professional ethics laws.
A)clearly does not mean that people really are fully rational and self-interested all the time.
B)clearly means that people really are fully rational and self-interested all the time.
C)is a practice never followed by economists but is often followed by psychologists.
D)is a practice always followed by behavioral economists.
E)is a practice that is banned in most states by professional ethics laws.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
6
Most state lotteries:
A)have positive expected values.
B)have negative expected values.
C)have expected values equal to zero.
D)do not have expected values because state lotteries are not games of chance.
E)do not have expected values because most state lotteries are operated by government agencies.
A)have positive expected values.
B)have negative expected values.
C)have expected values equal to zero.
D)do not have expected values because state lotteries are not games of chance.
E)do not have expected values because most state lotteries are operated by government agencies.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
7
Behavioral economics studies:
A)economy-wide phenomena such as real output,inflation,unemployment,and business cycles.
B)the decision-making processes of rational,self-interested economic actors.
C)all aspects of the markets and institutions that make up the financial system.
D)the implications of trade among individuals,firms,and countries.
E)how human psychology influences the decision-making process.
A)economy-wide phenomena such as real output,inflation,unemployment,and business cycles.
B)the decision-making processes of rational,self-interested economic actors.
C)all aspects of the markets and institutions that make up the financial system.
D)the implications of trade among individuals,firms,and countries.
E)how human psychology influences the decision-making process.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
8
The traditional economic model conceptualizes the economy as made up of infinitely calculating,unemotional maximizers that have been called:
A)Homo consumus.
B)Homo economicus.
C)Homo microcus.
D)Homo demandcurvius.
E)Homo elasticious.
A)Homo consumus.
B)Homo economicus.
C)Homo microcus.
D)Homo demandcurvius.
E)Homo elasticious.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
9
In 2002,Daniel Kahneman was awarded the Nobel Prize in Economics for "having integrated insights from psychological research into economic science,especially concerning human judgment and decision-making under uncertainty." Source: "The Price in Economics 2002: Press Release." Nobelprize.org.12 Oct 2012.www.nobelprize.org/nobel_prizes/economics/laureates/2002/press.html
Based on this information,which academic field would Daniel Kahneman most likely identify with?
A)economics
B)industrial-organizational sociology
C)evolutionary biology
D)English
E)behavioral economics
Based on this information,which academic field would Daniel Kahneman most likely identify with?
A)economics
B)industrial-organizational sociology
C)evolutionary biology
D)English
E)behavioral economics

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
10
A consumer who adheres to bounded rationality is:
A)a fully rational consumer who behaves like an all-knowing supercomputer when making cost-benefit calculations.
B)a completely irrational consumer who is unable to use logic to compare costs and benefits.
C)neither capable of performing the problem-solving that traditional economic theory assumes nor is inclined to do so.
D)rational only in situations that involve market prices.
E)never rational in situations that involve market prices.
A)a fully rational consumer who behaves like an all-knowing supercomputer when making cost-benefit calculations.
B)a completely irrational consumer who is unable to use logic to compare costs and benefits.
C)neither capable of performing the problem-solving that traditional economic theory assumes nor is inclined to do so.
D)rational only in situations that involve market prices.
E)never rational in situations that involve market prices.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
11
Behavioral economics seeks to dethrone __________ and replace him with something "more human."
A)Homo rationalimus
B)Homo economicus
C)Homo macrus
D)Homo sapiens
E)Homo stevejobsimus
A)Homo rationalimus
B)Homo economicus
C)Homo macrus
D)Homo sapiens
E)Homo stevejobsimus

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
12
When comparing the standard models in the respective fields of economics and psychology,it is clear that:
A)both economists and psychologists always assume that people behave in a fully rational way.
B)both economists and psychologists always assume that people do not act in a fully rational way.
C)neither economists nor psychologists always assume that people behave in a fully rational way.
D)economists generally assume that people behave in a rational way,whereas psychologists generally do not.
E)psychologists generally assume that people behave in a rational way,whereas economists generally do not.
A)both economists and psychologists always assume that people behave in a fully rational way.
B)both economists and psychologists always assume that people do not act in a fully rational way.
C)neither economists nor psychologists always assume that people behave in a fully rational way.
D)economists generally assume that people behave in a rational way,whereas psychologists generally do not.
E)psychologists generally assume that people behave in a rational way,whereas economists generally do not.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
13
__________ is the field of economics that studies how human psychology influences the decision-making process.
A)Public finance
B)Psychology
C)Behavioral economics
D)Sociology
E)Macroeconomics
A)Public finance
B)Psychology
C)Behavioral economics
D)Sociology
E)Macroeconomics

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following is an example of a game of chance?
A)Jeremiah plays basketball with his girlfriend.
B)Joan works eight hours at Taco Bell.
C)Jacqueline buys a lottery ticket.
D)John runs in a marathon.
E)Jalisha purchases salsa dancing shoes.
A)Jeremiah plays basketball with his girlfriend.
B)Joan works eight hours at Taco Bell.
C)Jacqueline buys a lottery ticket.
D)John runs in a marathon.
E)Jalisha purchases salsa dancing shoes.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
15
Behavioral economists draw on insights from __________ to explore how people behave in economic settings.
A)experimental psychology
B)experimental biology
C)evolutionary biology
D)astrology
E)theoretical physics
A)experimental psychology
B)experimental biology
C)evolutionary biology
D)astrology
E)theoretical physics

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
16
Whenever consumers make decisions without perfect information,the decision reflects:
A)perfect rationality.
B)perfect irrationality.
C)bounded rationality.
D)unbounded rationality.
E)confounded rationality.
A)perfect rationality.
B)perfect irrationality.
C)bounded rationality.
D)unbounded rationality.
E)confounded rationality.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
17
In 1990,Richard Thaler,a behavioral economist,said the following with respect to the standard economic model: The problem seems to be that while economists have gotten increasingly sophisticated and clever,consumers have remained decidedly human.
Which statement below best describes what Thaler implies in this sentence?
A)The standard economic model should be dumbed down so that more citizens can understand it.
B)The standard economic model fails to account for the fact that human beings generally do not act like Homo economicus.
C)Economists should educate citizens to become more sophisticated and clever so that their actions better fit the standard economic model.
D)The behavioral economic model needs to be abandoned.
E)Human nature is neither clever nor sophisticated.
Which statement below best describes what Thaler implies in this sentence?
A)The standard economic model should be dumbed down so that more citizens can understand it.
B)The standard economic model fails to account for the fact that human beings generally do not act like Homo economicus.
C)Economists should educate citizens to become more sophisticated and clever so that their actions better fit the standard economic model.
D)The behavioral economic model needs to be abandoned.
E)Human nature is neither clever nor sophisticated.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
18
In 2011,Edward Cartwright,a behavioral economist,gave credit to the Nobel Prize-winning economist Herbert Simon for launching what Cartwright calls the "you cannot be serious attack" on the standard economic model.Cartwright cites a paper published by Simon in 1955 where the author uses the standard economic model to solve elegantly how a rational person should behave.After solving an equation for this rational person's optimal behavior,Simon states: My first empirical proposition is that there is a complete lack of evidence that,in actual human choice situations of any complexity,these computations can be,or are in fact,performed.
Source: "A Behavior Model of Rational Choice." The Quarterly Journal of Economics (1955),page 104.
This statement by Simon can be best described as a call to:
A)governments for increased education spending so that more decision-makers can and will perform the computations that Simon is referring to.
B)citizens to do their part to reduce the complexity of all human choice situations.
C)economists to replace Homo economicus in economic thinking with something more humanlike.
D)economists to continue to use Homo economicus to guide their understanding of the complex nature of human decision-making.
E)the United States Department of Economic Rationality to impose a new bylaw prohibiting the use of the standard economic model in academic research papers.
Source: "A Behavior Model of Rational Choice." The Quarterly Journal of Economics (1955),page 104.
This statement by Simon can be best described as a call to:
A)governments for increased education spending so that more decision-makers can and will perform the computations that Simon is referring to.
B)citizens to do their part to reduce the complexity of all human choice situations.
C)economists to replace Homo economicus in economic thinking with something more humanlike.
D)economists to continue to use Homo economicus to guide their understanding of the complex nature of human decision-making.
E)the United States Department of Economic Rationality to impose a new bylaw prohibiting the use of the standard economic model in academic research papers.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
19
The standard economic model assumes people can be approximated by __________,who is assumed to be fully rational,calculating,and selfish; has unlimited computational ability; and never makes systematic mistakes.
A)Homo consumus
B)Homo microcus
C)Homo demandcurvius
D)Homo economicus
E)Homo elasticious
A)Homo consumus
B)Homo microcus
C)Homo demandcurvius
D)Homo economicus
E)Homo elasticious

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following activities involve Mary playing a game of chance?
A)Mary works eight hours at Dairy Queen and earns a total of $60.
B)Mary spends $250 on a used video game console.
C)Mary wins a $1,000 Visa gift card in a competitive food-eating competition.
D)Mary wins a $500 prize in a business-plan competition.
E)Mary deposits $5 in a slot machine and does not win anything.
A)Mary works eight hours at Dairy Queen and earns a total of $60.
B)Mary spends $250 on a used video game console.
C)Mary wins a $1,000 Visa gift card in a competitive food-eating competition.
D)Mary wins a $500 prize in a business-plan competition.
E)Mary deposits $5 in a slot machine and does not win anything.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win the 1-oz.gold bar?
A)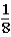
B)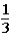
C)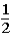
D)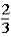
E)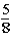
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win the 1-oz.gold bar?
A)
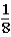
B)
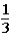
C)
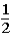
D)
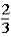
E)
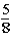

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win the 5-oz.gold bar?
A)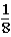
B)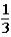
C)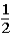
D)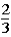
E)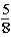
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win the 5-oz.gold bar?
A)
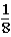
B)
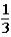
C)
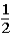
D)
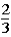
E)
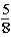

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
In the context of behavioral economics,the belief that outcomes that have not occurred in the recent past are more likely to occur soon,and that recent outcomes are unlikely to be repeated in the near future is best referred to as the:
A)gambler's fallacy.
B)base-rate fallacy.
C)existential fallacy.
D)hot-hand fallacy.
E)broken-window fallacy.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
In the context of behavioral economics,the belief that outcomes that have not occurred in the recent past are more likely to occur soon,and that recent outcomes are unlikely to be repeated in the near future is best referred to as the:
A)gambler's fallacy.
B)base-rate fallacy.
C)existential fallacy.
D)hot-hand fallacy.
E)broken-window fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the expected value of the game? Assume that the market price of gold is $1,000.00 per ounce.
A)$4,000.00
B)$2,333.33
C)$3,666.67
D)$5,000.00
E)$1,000.00
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the expected value of the game? Assume that the market price of gold is $1,000.00 per ounce.
A)$4,000.00
B)$2,333.33
C)$3,666.67
D)$5,000.00
E)$1,000.00

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If the contestant changes buckets from the original bucket to one of the other buckets remaining,the expected value of the game rises from:
A)$10.00 to $32.50.
B)$32.50 to $43.75.
C)$43.75 to $66.25.
D)$66.25 to $67.50.
E)$100.00 to $167.50.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If the contestant changes buckets from the original bucket to one of the other buckets remaining,the expected value of the game rises from:
A)$10.00 to $32.50.
B)$32.50 to $43.75.
C)$43.75 to $66.25.
D)$66.25 to $67.50.
E)$100.00 to $167.50.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose a casino is offering a game of chance where Sally can bet $5 on the flip of a fair coin.If the casino employee flips tails,Sally loses the $5 that she bet.If the casino employee flips heads,Sally receives a payout of $11 (the $5 she originally bet plus another $6).If Sally sits in the casino and plays this game 1,000 times consecutively over a period of 12 hours,she:
A)will likely end up with less money than she started with.
B)will likely end up with more money than she started with.
C)will likely end up with the same amount of money that she started with.
D)is equally likely to end up with more money or less money than she started with.
E)will definitely end up with less money than she started with.
A)will likely end up with less money than she started with.
B)will likely end up with more money than she started with.
C)will likely end up with the same amount of money that she started with.
D)is equally likely to end up with more money or less money than she started with.
E)will definitely end up with less money than she started with.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
The contestant changes buckets from the original bucket to the other bucket remaining.This change of buckets changes the probability that the contestant will win the 5-oz.gold bar from _____________.
A)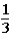 to
to 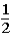
B)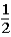 to
to 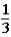
C)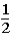 to
to 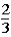
D)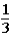 to
to 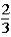
E)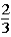 to
to 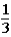
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
The contestant changes buckets from the original bucket to the other bucket remaining.This change of buckets changes the probability that the contestant will win the 5-oz.gold bar from _____________.
A)
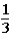 to
to 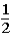
B)
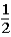 to
to 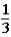
C)
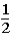 to
to 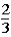
D)
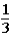 to
to 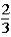
E)
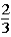 to
to 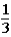

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If the contestant changes buckets from the original bucket to one of the other buckets remaining,what is the probability that the contestant will win the $100 bill?
A)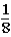
B)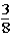
C)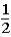
D)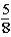
E)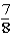
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If the contestant changes buckets from the original bucket to one of the other buckets remaining,what is the probability that the contestant will win the $100 bill?
A)
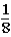
B)
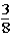
C)
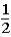
D)
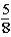
E)

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win the 1-oz.gold bar?
A)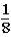
B)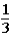
C)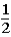
D)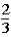
E)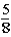
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win the 1-oz.gold bar?
A)
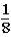
B)
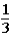
C)
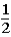
D)
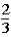
E)
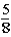

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win the stack of $100 bills?
A)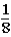
B)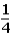
C)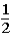
D)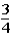
E)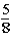
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win the stack of $100 bills?
A)
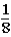
B)
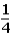
C)
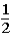
D)
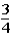
E)
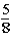

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant will receive the gold bar that is under his or her bucket. The host of the game show asks the contestant to choose one of the three buckets.The contestant chooses bucket #1.After the contestant makes a choice,the host lifts up bucket #2 to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose (bucket #1)and the bucket that was not uncovered by the host (bucket #3).
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.The contestant changes buckets from the original bucket (bucket #1)to the other bucket remaining (bucket #3).When the contestant originally made the choice of bucket #1,the probability of the 5-oz.gold bar being under that bucket was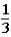 .This means that the probability of the 5-oz.gold bar being under either bucket #1 or bucket #2 was
.This means that the probability of the 5-oz.gold bar being under either bucket #1 or bucket #2 was 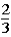 .When the host lifted bucket #2 to reveal a 1-oz.gold bar under it,the probability of the 5-oz.gold bar being under bucket #3 is now ____________,while the probability of the 5-oz.gold bar being under bucket number #1 is still _____________.
.When the host lifted bucket #2 to reveal a 1-oz.gold bar under it,the probability of the 5-oz.gold bar being under bucket #3 is now ____________,while the probability of the 5-oz.gold bar being under bucket number #1 is still _____________.
A)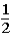 ;
; 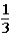
B)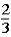 ;
; 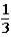
C)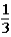 ;
; 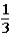
D)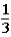 ;
; 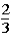
E)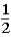 ;
; 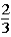
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant will receive the gold bar that is under his or her bucket. The host of the game show asks the contestant to choose one of the three buckets.The contestant chooses bucket #1.After the contestant makes a choice,the host lifts up bucket #2 to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose (bucket #1)and the bucket that was not uncovered by the host (bucket #3).
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.The contestant changes buckets from the original bucket (bucket #1)to the other bucket remaining (bucket #3).When the contestant originally made the choice of bucket #1,the probability of the 5-oz.gold bar being under that bucket was
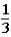 .This means that the probability of the 5-oz.gold bar being under either bucket #1 or bucket #2 was
.This means that the probability of the 5-oz.gold bar being under either bucket #1 or bucket #2 was 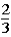 .When the host lifted bucket #2 to reveal a 1-oz.gold bar under it,the probability of the 5-oz.gold bar being under bucket #3 is now ____________,while the probability of the 5-oz.gold bar being under bucket number #1 is still _____________.
.When the host lifted bucket #2 to reveal a 1-oz.gold bar under it,the probability of the 5-oz.gold bar being under bucket #3 is now ____________,while the probability of the 5-oz.gold bar being under bucket number #1 is still _____________.A)
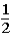 ;
; 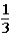
B)
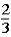 ;
; 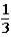
C)
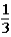 ;
; 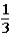
D)
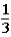 ;
; 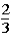
E)
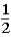 ;
; 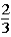

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
32
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win exactly one $5 bill?
A)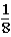
B)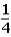
C)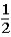
D)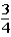
E)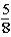
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket chosen,what is the probability that the contestant will win exactly one $5 bill?
A)
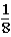
B)
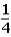
C)
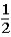
D)
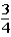
E)
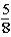

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose a casino is offering a game of chance where Frank can bet $6 on the flip of a fair coin.If the casino employee flips tails,Frank loses the $6 that he bet.If the casino employee flips heads,Frank receives a payout of $11 (the $6 he originally bet plus another $5).If Frank sits in the casino and plays this game 1,000 times consecutively over a period of 12 hours,he:
A)will likely end up with less money than he started with.
B)will likely end up with more money than he started with.
C)will likely end up with the same amount of money that he started with.
D)is equally likely to end up with more money or less money than he started with.
E)will definitely end up with less money than he started with.
A)will likely end up with less money than he started with.
B)will likely end up with more money than he started with.
C)will likely end up with the same amount of money that he started with.
D)is equally likely to end up with more money or less money than he started with.
E)will definitely end up with less money than he started with.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win the 5-oz.gold bar?
A)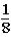
B)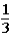
C)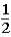
D)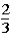
E)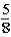
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win the 5-oz.gold bar?
A)
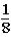
B)
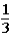
C)
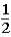
D)
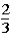
E)
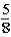

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win the stack of $100 bills?
A)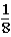
B)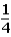
C)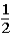
D)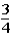
E)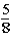
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win the stack of $100 bills?
A)
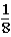
B)
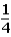
C)
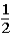
D)
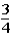
E)
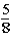

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If the contestant changes buckets from the original bucket to one of the other buckets remaining,what is the expected value of the game?
A)$32.50
B)$40.00
C)$43.75
D)$66.25
E)$100.00
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If the contestant changes buckets from the original bucket to one of the other buckets remaining,what is the expected value of the game?
A)$32.50
B)$40.00
C)$43.75
D)$66.25
E)$100.00

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is exactly one $100 bill.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the expected value of the game?
A)$5.00
B)$95.00
C)$62.50
D)$28.75
E)$76.25
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is exactly one $100 bill.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the expected value of the game?
A)$5.00
B)$95.00
C)$62.50
D)$28.75
E)$76.25

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,the expected value of the game is __________; if the contestant does not change buckets and sticks with the original bucket chosen,the expected value of the game is ___________.Assume that the market price of gold is $1,000.00 per ounce.
A)$4,000.00; $4,000.00
B)$2,333.33; $3666.67
C)$3,666.67; $2333.33
D)$5,000.00; $1,000.00
E)$1,000.00; $5,000.00
Imagine a game show on television where one lucky contestant is presented with three upside-down buckets that are numbered 1,2,and 3.Under one of the buckets is a 5-oz.gold bar.Under each of the other two buckets is a 1-oz.gold bar.After the game ends,the contestant receives the gold bar that is under his or her bucket.
The host of the game show asks the contestant to choose one of the three buckets.After the contestant makes a choice,the host lifts up one of the remaining two buckets to reveal a 1-oz.gold bar under it.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,the expected value of the game is __________; if the contestant does not change buckets and sticks with the original bucket chosen,the expected value of the game is ___________.Assume that the market price of gold is $1,000.00 per ounce.
A)$4,000.00; $4,000.00
B)$2,333.33; $3666.67
C)$3,666.67; $2333.33
D)$5,000.00; $1,000.00
E)$1,000.00; $5,000.00

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win exactly one $5 bill?
A)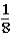
B)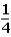
C)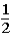
D)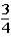
E)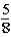
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a large pile of $100 bills.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant changes buckets from the original bucket to the other bucket remaining,what is the probability that the contestant will win exactly one $5 bill?
A)
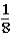
B)
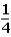
C)
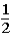
D)
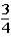
E)
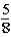

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
40
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is exactly one $100 bill.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket,what is the expected value of the game?
A)$5.00
B)$95.00
C)$62.50
D)$28.75
E)$76.25
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is exactly one $100 bill.Under each of the other three buckets is exactly one $5 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts up two of the remaining three buckets to reveal a $5 bill under each of them.At this point,only two buckets remain uncovered: the bucket that the contestant originally chose and the bucket that was not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to the only other bucket remaining.
If the contestant does not change buckets and stays with the original bucket,what is the expected value of the game?
A)$5.00
B)$95.00
C)$62.50
D)$28.75
E)$76.25

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If 12 consecutive tosses of a fair coin have all been tails,some individuals tend to think that the next one "must be heads." This is an example of the:
A)casino's fallacy.
B)dealer's fallacy.
C)gambler's fallacy.
D)masked-man fallacy.
E)hot-hand fallacy.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If 12 consecutive tosses of a fair coin have all been tails,some individuals tend to think that the next one "must be heads." This is an example of the:
A)casino's fallacy.
B)dealer's fallacy.
C)gambler's fallacy.
D)masked-man fallacy.
E)hot-hand fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
42
The opposite of the gambler's fallacy is the:
A)hot-hand fallacy.
B)historian's fallacy.
C)fallacy of single cause.
D)dealer's fallacy.
E)mind-projection fallacy.
A)hot-hand fallacy.
B)historian's fallacy.
C)fallacy of single cause.
D)dealer's fallacy.
E)mind-projection fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
In the context of behavioral economics,the belief that outcomes that have not occurred in the recent past are __________ likely to occur soon,and that recent outcomes are __________ to be repeated in the near future is best referred to as the gambler's fallacy.
A)more; likely
B)more; unlikely
C)less; likely
D)less; unlikely
E)less; never going
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
In the context of behavioral economics,the belief that outcomes that have not occurred in the recent past are __________ likely to occur soon,and that recent outcomes are __________ to be repeated in the near future is best referred to as the gambler's fallacy.
A)more; likely
B)more; unlikely
C)less; likely
D)less; unlikely
E)less; never going

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
44
When people want to maintain their current lifestyles and are reluctant to change,they may exhibit what is known as the:
A)hot-hand fallacy.
B)gambler's fallacy.
C)status quo bias.
D)hot-hand bias.
E)gambler's bias.
A)hot-hand fallacy.
B)gambler's fallacy.
C)status quo bias.
D)hot-hand bias.
E)gambler's bias.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose a student tosses a fair coin consecutively seven times and gets tails each time.Which belief about the probability of getting tails on the next toss is not consistent with the hot-hand fallacy?
A)The probability of getting heads on the next toss is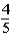 .
.
B)The probability of getting heads on the next toss is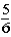 .
.
C)The probability of getting heads on the next toss is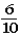 .
.
D)The probability of getting heads on the next toss is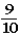 .
.
E)The probability of getting heads on the next toss is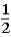 .
.
A)The probability of getting heads on the next toss is
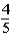 .
.B)The probability of getting heads on the next toss is
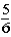 .
.C)The probability of getting heads on the next toss is
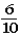 .
.D)The probability of getting heads on the next toss is
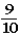 .
.E)The probability of getting heads on the next toss is
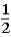 .
.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
46
___________ occur when the ordering of the questions that are asked influences the answers.
A)Rational expectations
B)Hot-hand effects
C)Fairness effects
D)Priming effects
E)Quasi-rational effects
A)Rational expectations
B)Hot-hand effects
C)Fairness effects
D)Priming effects
E)Quasi-rational effects

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
47
If 12 consecutive tosses of a fair coin have all been tails,some individuals tend to think that the next one "must be tails." This is an example of the:
A)casino's fallacy.
B)dealer's fallacy.
C)gambler's fallacy.
D)masked-man fallacy.
E)hot-hand fallacy.
A)casino's fallacy.
B)dealer's fallacy.
C)gambler's fallacy.
D)masked-man fallacy.
E)hot-hand fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose a student tosses a fair coin consecutively ten times and gets tails each time.Which belief about the probability of getting heads on the next toss is not consistent with the gambler's fallacy?
A)The probability of getting heads on the next toss is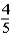 .
.
B)The probability of getting heads on the next toss is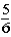 .
.
C)The probability of getting heads on the next toss is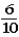 .
.
D)The probability of getting heads on the next toss is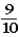 .
.
E)The probability of getting heads on the next toss is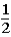 .
.
A)The probability of getting heads on the next toss is
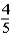 .
.B)The probability of getting heads on the next toss is
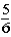 .
.C)The probability of getting heads on the next toss is
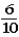 .
.D)The probability of getting heads on the next toss is
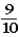 .
.E)The probability of getting heads on the next toss is
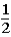 .
.
Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose a student tosses a fair coin consecutively ten times and gets tails each time.If the student concludes that the next toss will be heads because heads "is due," the student has committed the:
A)hot-hand fallacy.
B)casino's fallacy.
C)gambler's fallacy.
D)dealer's fallacy.
E)NBA fallacy.
A)hot-hand fallacy.
B)casino's fallacy.
C)gambler's fallacy.
D)dealer's fallacy.
E)NBA fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
50
A finding of no significant difference in 401(k)plan participation after the plan change provides evidence that employee 401(k)participation decisions are made ___________ effects do not exist in the context of 401(k)plan participation.
A)rationally and rational
B)irrationally and priming
C)rationally and framing
D)irrationally and framing
E)rationally and fairness
A)rationally and rational
B)irrationally and priming
C)rationally and framing
D)irrationally and framing
E)rationally and fairness

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
51
In the 1990s,researchers Clotfelter,Cook,and Terrel analyzed data from a particular game that was offered in both the Maryland and New Jersey state lotteries.In the game,participants place a bet and then guess a three-digit number.After all bets have been placed,a three-digit number is randomly drawn by state lottery representatives.If a bettor correctly guesses the number drawn,the bettor wins a large prize.Consistent with the ___________,the researchers found clear evidence that lottery players bet less often on a number that had won in the recent past.
A)hot-hand fallacy
B)gambler's fallacy
C)casino's fallacy
D)genetic fallacy
E)naturalistic fallacy
A)hot-hand fallacy
B)gambler's fallacy
C)casino's fallacy
D)genetic fallacy
E)naturalistic fallacy

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
52
If 25 consecutive tosses of a fair coin have all been heads,some individuals tend to think that the next one "must be heads." This is an example of the:
A)hot-hand fallacy.
B)continuum fallacy.
C)broken-window fallacy.
D)definist fallacy.
E)gambler's fallacy.
A)hot-hand fallacy.
B)continuum fallacy.
C)broken-window fallacy.
D)definist fallacy.
E)gambler's fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
53
In the 1990s,researchers Clotfelter,Cook,and Terrel analyzed data from a particular game of chance that was offered in both the Maryland and New Jersey state lotteries.In the game,participants place a bet and then guessed a three-digit number.After all bets have been placed,a three-digit number is randomly drawn by state lottery representatives.If a bettor correctly guesses the number drawn,the bettor wins a large prize.The researchers found clear evidence that lottery players bet less on a number that had won in the recent past.This finding indicates that the __________ is not at work.
A)hot-hand fallacy
B)gambler's fallacy
C)casino's fallacy
D)genetic fallacy
E)naturalistic fallacy
A)hot-hand fallacy
B)gambler's fallacy
C)casino's fallacy
D)genetic fallacy
E)naturalistic fallacy

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
54
Corey and Trevor are playing a coin-tossing game where each player,in turn,tosses a fair coin consecutively ten times.The winner of the game is the player who tosses the most consecutive tails.Corey decides to go first and tosses tails five times in a row.Ricky and Julian are observing the game and have the following conversation before Corey attempts the sixth toss: Ricky: "The probability of Corey tossing tails has to be greater than 75% because he is on a roll!"
Julian: "No,Ricky,the probability of Corey tossing tails has to be less than 25% because he is due to toss heads."
Ricky's statement is an example of __________,and Julian's statement is an example of ____________.
A)the hot-hand fallacy; the hot-hand fallacy
B)the gambler's fallacy; the gambler's fallacy
C)the hot-hand fallacy; the gambler's fallacy
D)the gambler's fallacy; the hot-hand fallacy
E)neither the gambler's fallacy nor the hot-hand fallacy; the gambler's fallacy
Julian: "No,Ricky,the probability of Corey tossing tails has to be less than 25% because he is due to toss heads."
Ricky's statement is an example of __________,and Julian's statement is an example of ____________.
A)the hot-hand fallacy; the hot-hand fallacy
B)the gambler's fallacy; the gambler's fallacy
C)the hot-hand fallacy; the gambler's fallacy
D)the gambler's fallacy; the hot-hand fallacy
E)neither the gambler's fallacy nor the hot-hand fallacy; the gambler's fallacy

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
55
In behavioral economics,the status quo bias is often accompanied by ___________,which exists when a person places more value on avoiding losses than attempting to realize gains.
A)loss aversion
B)gain aversion
C)the ambiguity effect
D)the availability heuristic
E)the bandwagon effect
A)loss aversion
B)gain aversion
C)the ambiguity effect
D)the availability heuristic
E)the bandwagon effect

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
56
Nancy tosses a fair coin five times and gets heads each time.When her son Shane asks her about the probability of getting tails on the next (sixth)toss,Nancy says the following: "This is a fair coin,so I should toss heads approximately 50% of the time.Because I have tossed heads 100% of the time for my first five tosses,then the probability of me tossing tails on the sixth toss must be greater than 50%." Nancy's statement is an example of the:
A)hot-hand fallacy.
B)association fallacy.
C)gambler's fallacy.
D)dealer's fallacy.
E)Showtime fallacy.
A)hot-hand fallacy.
B)association fallacy.
C)gambler's fallacy.
D)dealer's fallacy.
E)Showtime fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
57
Corey and Trevor are playing a coin-tossing game where each player,in turn,tosses a fair coin consecutively ten times.The winner of the game is the player who tosses the most consecutive tails.Corey decides to go first and tosses tails five times in a row.Ricky and Julian are observing the game,and Ricky whispers the following to Julian before Corey attempts the sixth toss: "The probability of Corey tossing tails has to be greater than 75% because he is on a roll!" Ricky's statement is an example of the:
A)Rickyism fallacy.
B)fallacy of single cause.
C)Sunnyvale fallacy
D)hot-hand fallacy.
E)gambler's fallacy.
A)Rickyism fallacy.
B)fallacy of single cause.
C)Sunnyvale fallacy
D)hot-hand fallacy.
E)gambler's fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
58
Bart and Lisa are playing a coin-tossing game where each player tosses a fair coin 20 times consecutively.The winner of the game is the player who tosses the most consecutive tails.Bart decides to go first and tosses tails five times in a row.Marge and Homer are observing the game and make the following observations before Bart attempts the sixth toss: Marge: "The probability of Bart tossing tails has to be greater than 75% because he is on a roll!"
Homer: "No,Marge,the probability of Bart tossing tails has to be less than 25% because he hasn't tossed heads in the last five tosses and he is due to toss heads!"
A behavioral economist would conclude that Marge's statement is an example of the __________,and Homer's statement is an example of the ___________.
A)continuum fallacy; hot-hand fallacy
B)hot-hand fallacy; broken-window fallacy
C)gambler's fallacy; hot-hand fallacy
D)hot-hand fallacy; gambler's fallacy
E)behavior fallacy; broken-window fallacy
Homer: "No,Marge,the probability of Bart tossing tails has to be less than 25% because he hasn't tossed heads in the last five tosses and he is due to toss heads!"
A behavioral economist would conclude that Marge's statement is an example of the __________,and Homer's statement is an example of the ___________.
A)continuum fallacy; hot-hand fallacy
B)hot-hand fallacy; broken-window fallacy
C)gambler's fallacy; hot-hand fallacy
D)hot-hand fallacy; gambler's fallacy
E)behavior fallacy; broken-window fallacy

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the following scenario to answer the questions that follow.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If 25 consecutive tosses of a fair coin have all been heads,some individuals tend to think that the next one "must be tails." This is an example of the:
A)hot-hand fallacy.
B)continuum fallacy.
C)broken-window fallacy.
D)definist fallacy.
E)gambler's fallacy.
Imagine a game show on television where one lucky contestant is presented with four upside-down buckets that are numbered 1,2,3,and 4.Under one of the buckets is a $100 bill.Under each of the other three buckets is a $10 bill.After the game ends,the contestant will receive the amount of money that is under his or her bucket.
The host of the game show asks the contestant to choose one of the four buckets.After the contestant makes a choice,the host lifts one of the remaining three buckets to reveal a $10 bill under it.At this point,three buckets remain uncovered: the bucket that the contestant originally chose and the two buckets that were not uncovered by the host.
The host subsequently asks the contestant if he or she would like to keep the original bucket or change buckets to one of the two other buckets remaining.
If 25 consecutive tosses of a fair coin have all been heads,some individuals tend to think that the next one "must be tails." This is an example of the:
A)hot-hand fallacy.
B)continuum fallacy.
C)broken-window fallacy.
D)definist fallacy.
E)gambler's fallacy.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
60
A ___________ effect occurs when an answer depends on how a question is asked or when a decision is influenced by the way alternatives are presented.
A)framing
B)hot-hand
C)Hayekian
D)priming
E)behaviorist
A)framing
B)hot-hand
C)Hayekian
D)priming
E)behaviorist

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
61
___________ exists when a person places more value on avoiding losses than attempting to realize gains.
A)The availability heuristic
B)Loss aversion
C)The trait ascription bias
D)The halo effect
E)The availability cascade
A)The availability heuristic
B)Loss aversion
C)The trait ascription bias
D)The halo effect
E)The availability cascade

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
62
The standard economic model of consumer choice assumes that people are __________.
A)risk averse.
B)risk loving.
C)risk neutral.
D)fairness averse.
E)fairness loving.
A)risk averse.
B)risk loving.
C)risk neutral.
D)fairness averse.
E)fairness loving.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
63
John and Rebecca are playing an ultimatum game where John is given $100.00 and asked to propose a way of splitting it with Rebecca.When Rebecca learns John's proposal,she chooses whether to accept or reject the split.If Rebecca accepts the split,both players receive the money according to John's split proposal.If Rebecca rejects the split,both players receive nothing.This game will be played only once,so John does not have to worry about reciprocity when making his choice. Suppose that John proposes a split such that John will receive $99.99 and Rebecca will receive $0.01.Traditional economic theory predicts that Rebecca will:
A)accept the $0.01 because she values receiving $0.01 more than receiving nothing.
B)accept the $0.01 because she wishes to punish John for proposing such an unfair split.
C)reject the $0.01 because she wishes to punish John for proposing such an unfair split.
D)reject the $0.01 and also would have rejected a split such that John receives $50.00 and Rebecca receives $50.00.
E)sometimes accept the $0.01 and sometimes reject the $0.01,depending on her mood at the time.
A)accept the $0.01 because she values receiving $0.01 more than receiving nothing.
B)accept the $0.01 because she wishes to punish John for proposing such an unfair split.
C)reject the $0.01 because she wishes to punish John for proposing such an unfair split.
D)reject the $0.01 and also would have rejected a split such that John receives $50.00 and Rebecca receives $50.00.
E)sometimes accept the $0.01 and sometimes reject the $0.01,depending on her mood at the time.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
64
At the beginning of a semester,a group of five students (Jim,Andy,Beth,Brandy,and Duane)were asked to order a snack that the teacher will deliver to the students free of charge before the first class of the tenth week of the semester.The three choices were an apple,a banana,or a Snickers candy bar.The teacher collected the orders and found that two students have ordered an apple,two students have ordered a banana,and one student has ordered a Snickers candy bar.The four students who ordered either an apple or a banana cited health consciousness as the reason for their choice. Immediately before the orders are scheduled to be delivered,the teacher informs the students that they can switch their choice and order something else from the original menu if they wish,or they can receive what they originally ordered.Which of the following scenarios is the best example of inconsistent intertemporal decision-making?
A)Jim originally ordered an apple and did not change his choice when prompted.
B)Andy ordered a banana and switched to an apple when prompted.
C)Beth ordered an apple and switched to a banana when prompted.
D)Brandy ordered a banana and switched to a Snickers candy bar when prompted.
E)Duane ordered a Snickers candy bar and did not change his choice when prompted.
A)Jim originally ordered an apple and did not change his choice when prompted.
B)Andy ordered a banana and switched to an apple when prompted.
C)Beth ordered an apple and switched to a banana when prompted.
D)Brandy ordered a banana and switched to a Snickers candy bar when prompted.
E)Duane ordered a Snickers candy bar and did not change his choice when prompted.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
65
Assume that Aaron and Jane are two experimental subjects who practice bounded rationality.If Aaron were to offer an unfair proposal,he would likely receive a payoff of __________,but if he were to offer a fair proposal,he would likely receive a payoff of __________.
A)$0; $0
B)$0; $999
C)$999; $0
D)$500; $0
E)$0; $500
A)$0; $0
B)$0; $999
C)$999; $0
D)$500; $0
E)$0; $500

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
66
The ___________ game is a common game that behavioral economists use in an experimental setting to study how fairness enters into the rational decision-making process.
A)ultimatum
B)prisoner's dilemma
C)behavioral economics
D)gambler's dilemma
E)hawk-dove
A)ultimatum
B)prisoner's dilemma
C)behavioral economics
D)gambler's dilemma
E)hawk-dove

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
67
Which general observation can be inferred from the observation of real people playing the ultimatum game?
A)People care about looks.
B)People care about body image.
C)People care about voice tone.
D)People care about fairness.
E)People care about respect.
A)People care about looks.
B)People care about body image.
C)People care about voice tone.
D)People care about fairness.
E)People care about respect.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
68
Stephen C.has been purchasing Fruity Pebbles brand cereal each week for the past two years,even though a different brand,such as Captain Crunch or Rice Krispies,would in all likelihood bring him more utility per dollar spent.A behavioral economist would suspect Stephen C.is suffering from the ___________ bias.
A)choice-supportive
B)status quo
C)egocentric
D)time-saving
E)outcome
A)choice-supportive
B)status quo
C)egocentric
D)time-saving
E)outcome

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
69
If Aaron were to offer an unfair proposal,experimental results show that Jane would likely punish him by making herself:
A)worse off by $1 and rejecting his offer.
B)better off by $1 and rejecting his offer.
C)worse off by $999 and rejecting his offer.
D)worse off by $500 and rejecting his offer.
E)worse off by $1,000 and rejecting his offer.
A)worse off by $1 and rejecting his offer.
B)better off by $1 and rejecting his offer.
C)worse off by $999 and rejecting his offer.
D)worse off by $500 and rejecting his offer.
E)worse off by $1,000 and rejecting his offer.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
70
The ___________ game is an economic experiment in which two players decide how to divide a pot of money.
A)prisoner's dilemma
B)hawk-dove
C)behavioral economics
D)ultimatum
E)hot-hand dilemma
A)prisoner's dilemma
B)hawk-dove
C)behavioral economics
D)ultimatum
E)hot-hand dilemma

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
71
Proponents of fairness would likely believe that:
A)the poor should pay higher tax rates on their personal income than the rich do,a tax structure known as regressive taxation.
B)the rich should pay higher tax rates on their personal income than the poor do,a tax structure known as progressive taxation.
C)the poor should pay higher entrance fees to national parks whenever an entrance fee applies.
D)a bigger,less-equal economic pie is more favorable than a smaller,more-equal economic pie.
E)if the poor can receive free baby formula and diapers from the government,then the rich should also be able to receive free baby formula and diapers from the government.
A)the poor should pay higher tax rates on their personal income than the rich do,a tax structure known as regressive taxation.
B)the rich should pay higher tax rates on their personal income than the poor do,a tax structure known as progressive taxation.
C)the poor should pay higher entrance fees to national parks whenever an entrance fee applies.
D)a bigger,less-equal economic pie is more favorable than a smaller,more-equal economic pie.
E)if the poor can receive free baby formula and diapers from the government,then the rich should also be able to receive free baby formula and diapers from the government.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
72
If Aaron could be 100% certain that Jane was rational,did not care about fairness,and always made decisions to maximize her payoff regardless of the situation she might find herself in,Aaron would likely offer a(n):
A)unfair proposal and ultimately receive a payoff of $500.
B)unfair proposal and ultimately receive a payoff of $999.
C)unfair proposal and ultimately receive a payoff of $0.
D)fair proposal and ultimately receive a payoff of $500.
E)fair proposal and ultimately receive a payoff of $0.
A)unfair proposal and ultimately receive a payoff of $500.
B)unfair proposal and ultimately receive a payoff of $999.
C)unfair proposal and ultimately receive a payoff of $0.
D)fair proposal and ultimately receive a payoff of $500.
E)fair proposal and ultimately receive a payoff of $0.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
73
The ___________ bias leads decision-makers to try to protect what they have,even when an objective evaluation of their circumstances suggests that a change would be beneficial.
A)egocentric
B)choice-supportive
C)time-saving
D)status quo
E)outcome
A)egocentric
B)choice-supportive
C)time-saving
D)status quo
E)outcome

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
74
Jackie and Rhonda are playing an ultimatum game where Jackie is given $100 and asked to propose a way of splitting it with Rhonda.When Rhonda learns Jackie's proposal,Rhonda chooses whether to accept or reject the split.If Rhonda accepts the split,both players receive the money according to Jackie's split proposal.If Rhonda rejects the split,both players receive nothing.This game will be played only once,so Rhonda does not have to worry about reciprocity when making her choice.Traditional economic theory presumes that:
A)both players are irrational and wish to minimize the payoff to the other player.
B)both players are irrational and wish to maximize their own payoff.
C)both players are rational and wish to minimize their own payoff.
D)both players are rational and wish to maximize their own payoff.
E)the player that proposes the split is fully rational and wishes to maximize his or her own playoff,whereas the player that chooses to accept or reject the split is irrational and wishes to maximize the other player's payoff.
A)both players are irrational and wish to minimize the payoff to the other player.
B)both players are irrational and wish to maximize their own payoff.
C)both players are rational and wish to minimize their own payoff.
D)both players are rational and wish to maximize their own payoff.
E)the player that proposes the split is fully rational and wishes to maximize his or her own playoff,whereas the player that chooses to accept or reject the split is irrational and wishes to maximize the other player's payoff.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
75
People who are risk averse:
A)prefer a sure thing over a gamble with a higher expected value.
B)choose the outcome with the highest expected value.
C)choose the outcome with the lowest expected value.
D)prefer gambles with lower expected values,but potentially higher winnings,over a sure thing.
E)do not partake in any risky activities.
A)prefer a sure thing over a gamble with a higher expected value.
B)choose the outcome with the highest expected value.
C)choose the outcome with the lowest expected value.
D)prefer gambles with lower expected values,but potentially higher winnings,over a sure thing.
E)do not partake in any risky activities.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
76
The ___________ is a cognitive bias that leads people to prefer things to change as little as possible.
A)status quo bias
B)gambler's bias
C)hot-hand fallacy
D)gambler's fallacy
E)hot-hand bias
A)status quo bias
B)gambler's bias
C)hot-hand fallacy
D)gambler's fallacy
E)hot-hand bias

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
77
In 1980,the Schlitz Brewing Company conducted several beer taste tests on live television during NFL football games.One hundred confirmed Budweiser drinkers (who had each signed an affidavit stating that he drank at least 12 bottles of Budweiser each week)were each served a glass of both Schlitz and Budweiser in unmarked containers.After tasting both beers,the members of the group were asked which beer they preferred.Between 45% and 55% of the participants responded that they preferred Schlitz even though they were confirmed Budweiser drinkers. Which bias can likely explain why the participants in the group displayed such strong brand allegiance to Budweiser prior to the taste test?
A)the availability heuristic
B)the trait ascription bias
C)the availability cascade
D)status quo bias
E)the Rupertorian effect
A)the availability heuristic
B)the trait ascription bias
C)the availability cascade
D)status quo bias
E)the Rupertorian effect

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
78
Amanda and Brenda are considering playing a game called Matching Twenties.In this game,Amanda and Brenda will each place a $20 bill on the table.Both players will then toss a fair coin.If both Amanda and Brenda toss heads or both Amanda and Brenda toss tails,Amanda wins the $40 on the table.If one woman tosses heads and the other tosses tails,Brenda wins the $40 on the table. Amanda decides that she is not willing to play this game because a loss of $20 to Brenda would cause her to lose more utility than she would gain if she won $20 from Brenda.Which concept best explains Amanda's choice not to play the game?
A)hedonic editing
B)gain aversion
C)loss aversion
D)signaling
E)gain-loss asymmetry
A)hedonic editing
B)gain aversion
C)loss aversion
D)signaling
E)gain-loss asymmetry

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
79
For the past five years,John S.has been purchasing Citizens of Humanity brand jeans each time he needs a new pair of jeans,even though a different brand,such as RocaWear or Ecko,would in all likelihood bring him more utility per dollar spent.A behavioral economist would suspect John S.is suffering from the ___________ bias.
A)egocentric
B)choice-supportive
C)time-saving
D)status quo
E)outcome
A)egocentric
B)choice-supportive
C)time-saving
D)status quo
E)outcome

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck
80
Mario knows that,over the long run,it is in his best interest to save at least 10% of his paycheck for retirement.However,each time he receives his weekly paycheck of $1,000,he ends up spending it all and not depositing any to a retirement account.Mario has resolved to contact his employer's human resources department to set up a 401(k)work-sponsored retirement account where the 10% would be deducted automatically from his paycheck before it is issued to him each week.It is apparent from this information that Mario realized that:
A)his intertemporal decisions are inconsistent and he had to take action to make them consistent.
B)his intertemporal decisions are consistent and he had to take action to make them inconsistent.
C)it is better for him to handle sending money to a retirement account than to rely on his employer to send the money to a retirement account on his behalf.
D)he should not be saving for retirement after all because his short-run preferences to spend his entire paycheck are perfectly indicative of his long-run preferences.
E)he should not worry about the future anymore because it will take care of itself.
A)his intertemporal decisions are inconsistent and he had to take action to make them consistent.
B)his intertemporal decisions are consistent and he had to take action to make them inconsistent.
C)it is better for him to handle sending money to a retirement account than to rely on his employer to send the money to a retirement account on his behalf.
D)he should not be saving for retirement after all because his short-run preferences to spend his entire paycheck are perfectly indicative of his long-run preferences.
E)he should not worry about the future anymore because it will take care of itself.

Unlock Deck
Unlock for access to all 95 flashcards in this deck.
Unlock Deck
k this deck



