Deck 8: Rotational Motion of Solid Objects

Question 1

A flywheel is used to minimize changes in rotational velocity as the torque or the load changes. The rotational inertia of a flywheel should be chosen to be

A) anything-it doesn't matter.
B) as small as possible.
C) as large as possible.

Answer 1

as large as possible.

Question 2

You stand with your heels against a wall and bend ninety degrees forward at the waist.

A) You fall forward because your center of gravity moves ahead of your base of support.
B) You fall forward because of the momentum you gain when you move.
C) You are able to maintain your balance.
D) You fall forward because the muscles in your feet aren't strong enough to stop you.

Answer 2

You fall forward because your center of gravity moves ahead of your base of support.

Question 3

In a stable stack of identical boards at the edge of a table, the center of gravity of the top board

A) must lie above the table.
B) need not lie over anything.
C) must lie above the bottom board.
D) must lie above the next lower board.

Answer 3

must lie above the next lower board.

Question 4

The bigger diameter gears on the rear wheel of a multi-speed bike allow the rider to

A) increase the moment of inertia of the wheel.
B) exert more force on the wheel.
C) exert more torque on the wheel.
D) decrease the moment of inertia of the wheel.

Question 5

A torque acting on a body tends to produce

A) equilibrium.
B) linear velocity.
C) a new center of gravity.
D) angular rotation.

Question 6

Using a longer-handled wrench to loosen a tight nut allows you to

A) exert more force on the nut.
B) apply more torque to the nut.
C) increase the moment of inertia of the nut.
D) pull harder on the wrench.

Question 7

A constant torque is applied to a flywheel. Which of the following mechanical quantities will be constant?

A) Rotational energy
B) Angular momentum
C) Rotational velocity
D) Rotational acceleration
E) Linear velocity of a particle on the rim

Question 8

When a bicycle pedal is at the top of its motion, you can exert the greatest torque on the crank by

A) pushing straight down on the pedal with your foot.
B) hooking your toes under the pedal and pulling upward.
C) pushing straight forward on the pedal with your foot.

Question 9

Three different bodies-a uniform sphere, a uniform disk, and a hoop-all have same radius and same mass. The body with the largest rotational inertia will be

A) the sphere.
B) the disk.
C) the hoop.
D) none, as all have the same value of rotational inertia.

Question 10

The rotational inertia of an object depends on

A) its color.
B) how fast it is spinning.
C) how its mass is distributed about the spin axis.
D) the amount of torque applied to it.
E) none of these.

Question 11

Because the rotational inertia is higher, it is hardest in springboard diving to perform a forward somersault in

A) the straight position (no bending at knees or waist).
B) the pike position (bending at the waist but not the knees).
C) the tuck position (bending at both the waist and knees).

Question 12

A figure skater is spinning with her arms extended. She now pulls her arms close to her body. What happens?

A) Her angular acceleration decreases.
B) Her rotational inertia decreases.
C) The net external torque on her increases.
D) Her lever arm gets shorter.

Question 13

A hoop and a sphere have the same diameter and the same mass. Which one will have a larger rotational inertia?

A) The hoop.
B) The sphere.
C) Both will require the same time to reach the bottom.

Question 14

A dancer begins performing a pirouette with arms extended. (A pirouette is a complete spin about a vertical axis.) This motion is completed most easily when the rotational inertia is decreased by

A) bending at the waist at a right angle.
B) extending the arms and one leg straight out to the sides.
C) holding the arms straight up and extending one foot straight out to the side.
D) bringing the arms and legs in a line with the body.

Question 15

An isolated object is initially spinning at a constant speed. Then, although no external forces act upon it, its rotational speed increases. This must be due to

A) an increase in the moment of inertia.
B) an increase in the mass.
C) an increase in the angular momentum.
D) a decrease in the moment of inertia.
E) impossible, angular momentum conservation is violated.

Question 16

Three horses are side-by-side on a merry-go-round: one at the edge, one near the axis, and one in between. Each horse has the same angular speed. Which horse has the greatest linear speed?

A) The horse at the edge.
B) The horse in the middle.
C) The horse nearest the axis.
D) The linear speed is the same for all three horses.

Question 17

An object is moving in a horizontal circle, in a clockwise direction (as viewed from above). In which direction does its angular momentum vector point?

A) To the viewer's left
B) Away from the viewer
C) Toward the viewer
D) From the ball toward the center of the circle

Question 18

A solid disk and a hollow disk with the same mass and diameter are released together (from rest) to roll down an incline. The solid disk reaches the bottom first. From this information we can say that the angular acceleration was

A) larger for the hollow disk.
B) larger for the solid disk.
C) the same for both disks.
D) impossible to know without a measurement of time.

Question 19

A football thrown with a spinning motion is more stable than one thrown without spin because

A) there is no net torque on a spinning object.
B) air flows more easily around spinning objects.
C) the torque generated by the spinning action is conserved.
D) the angular momentum of a spinning object can only be changed by applying a torque.

Question 20

The angular momentum of an isolated object can be changed only by

A) changing its rotational inertia.
B) applying a torque.
C) applying a force along the axis of rotation.

Question 21

Which of the following is an appropriate unit for describing rotational acceleration?

A) m/s²
B) rad/min
C) rev/min
D) rev/m/s
E) rev/min²

Question 22

A solid disk and a hoop have different diameters but identical masses. Which one has a larger rotational inertia?

A) The solid disk.
B) The hoop.
C) It is impossible to know without knowing the diameters.
D) It is impossible to know without knowing the torques acting on the two objects.

Question 23

The angular momentum of a rotating body is conserved when

A) no net torque acts on the body.
B) no net force acts on the body.
C) when the body has a constant angular acceleration.
D) the shape of the body does not change.

Question 24

A merry-go-round, having a radius of 2.5 m, is set in motion starting from rest, by students applying a force of 500 N tangential to the rim of the wheel. After five seconds of torque, the students let go and measure the rotational speed: 1.25 rad/s. The rotational inertia of the merry-go-round is

A) 7.5 $\times$ 10² kg m².
B) 1.7 $\times$ 10³ kg m².
C) 2.5 $\times$ 10³ kg m².
D) 5.0 $\times$ 10³ kg m².
E) 1.0 $\times$ 10⁴ kg m².

Question 25

A gyroscope consists of a wheel mounted on an axle aligned along a north-south direction. The south end of the axle is suspended by a rope attached to the ceiling, and the north end is manually held at rest. The wheel is spinning rapidly, so that its angular momentum vector points north. Suddenly the north end is released. Since there is spin, the north end of the axle will begin to move

A) north.
B) east.
C) down.
D) west.
E) south.

Question 26

If you push directly on the handle of a closed door and it does not swing open, then

A) its rotational inertia must be much larger than your torque.
B) the net torque on the door must be zero.
C) the lever arm must be very small.
D) the angular momentum of the door is larger than your force.

Question 27

A moving bicycle exhibits less stability when the angular momentum of the wheels is less, which means

A) its forward speed is also slower.
B) its forward speed is faster.
C) the inverse of the forward speed equals the torque.

Question 28

The armature (or spinning portion) of a motor is accelerated uniformly from rest to a rotational velocity of 1500 rev/min in 10 seconds. The rotational acceleration of the motor is

A) 150 rad/s².
B) 15.7 rad/s².
C) 31.4 rad/s².
D) 75 rad/s².
E) zero.

Question 29

If there is a net torque on a wheel, then

A) there must be a net force on the wheel.
B) the wheel must have a nonzero angular acceleration.
C) the wheel cannot be spinning.
D) the angular momentum of the wheel cannot change direction.

Question 30

In using a long steel rod as a lever to move a large rock, where should the fulcrum be placed for a person to use the least amount of force to move the rock?

A) Close to the person.
B) Exactly halfway between the person and the rock.
C) Anywhere in between; it makes no difference.
D) Close to the rock.

Question 31

Torque in the metric system is measured in units of

A) N.
B) N s.
C) N rad.
D) N/m.
E) N m.

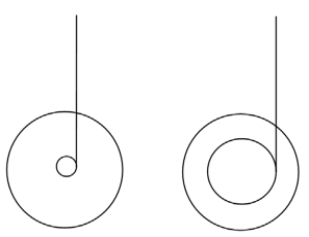
Question 32

The figure above shows two yo-yos that have the same mass and rotational inertia. The one on the right has a thicker axle than the one on the left. The torque produced by gravity is

A) larger for the yo-yo on the right.
B) larger for the yo-yo on the left.
C) the same for both yo-yos.
D) zero; there is no net torque on the yo-yos.

Question 33

A top of rotational inertia 4.0 kg m² receives a torque of 2.4 Nm from a physics professor. The angular acceleration of the body will be

A) 1.2 rev/s².
B) 6.0 rad/s².
C) 1.0 rad/s².
D) 6.0 rev/s².
E) 0.6 rad/s².

Question 34

If the net force on a body is zero, the net torque on the body is

A) always zero.
B) not necessarily zero.
C) certainly not zero.

Question 35

When an ice skater twirling on the point of a skate draws her arms in she ends up whirling faster. This is because

A) rotational energy is conserved.
B) linear momentum is conserved.
C) angular momentum is conserved.
D) a net external torque acts on the skater.

Question 36

A student plays on a see-saw with her experimental android robot, Robby. The student has a weight of 300 N and is seated 2.8 m from the axis of rotation. Robby balances her when he is seated 0.7 m from the axis. Robby's weight is

A) 1000 N.
B) 500 N.
C) 667 N.
D) 725 N.
E) 1200 N.

Question 37

It is possible using the analogies between linear motion and rotational motion to write an expression for rotational kinetic energy. The formula for rotational kinetic energy (assuming $\tau$ is torque, $\alpha$ is angular acceleration, I is rotational inertia, and $\omega$ is angular velocity) is

A) ½ $\tau$ $\alpha$ ².
B) ½ I $\alpha$ ².
C) ½ I $\omega$ ².
D) ½ $\tau$ $\omega$ ².

Question 38

A wheel is spinning on an axle. The linear velocity of a point on the rim is simply the product of the radius times the rotational velocity, as long as the rotational velocity is measured in units of

A) deg/s.
B) rev/min.
C) rad/s.
D) rev/s.
E) deg/min.

Question 39

The rotational velocity of a 45 rev/min phonograph record in rad/s is approximately

A) 45 rad/s.
B) 4.7 rad/s.
C) 0.75 rad/s.
D) 283 rad/s.
E) 15.7 rad/s.

Question 40

If the net torque on a body is zero, the net force on the body is

A) always zero.
B) not necessarily zero.
C) certainly not zero.

Question 41

If a solid disk and a hoop are to have the same mass and rotational inertia, then the hoop must have a _________ radius.

Question 42

The advantage that a lever can give you is that

A) with a small force, you can move a large weight.
B) with a small lever, you can move a large weight.
C) with a large force, you can torque a large weight.
D) with a small torque, you can lift a large weight.

Question 43

Holding out your hands sideways helps you keep your balance along a narrow set of stepping-stones because

A) the arms outward balance your weight.
B) arms inward only add to your weight.
C) with arms outward, you've increased your total rotational inertia relative to the pivot point: your feet.
D) moving the arms outward puts a counter-torque on the stepping-stones.
Fill in the Blank Questions

Question 44

The stability of a bicycle is due to angular momentum of the wheels when the bicycle is moving forward. The stability is due to the net angular momentum vector, which

A) points upward, perpendicular to the surface of Earth, thereby canceling the weight of the bicycle and rider.
B) points to the rider's left.
C) increases when the bicycle slows down due to conservation of energy.
D) is actually zero, since the back wheel cancels the angular momentum of the front wheel.

Question 45

Just as torque is the rotational analogue of force in linear motion, rotational inertia is the rotational analogue of _______ in linear motion.

Question 46

When a mechanic uses an extension arm on his wrench to loosen a stubborn nut, he is exerting additional torque because of an increase in the _________________ (two words) of the force.

Question 47

The angular momentum of a rotating body is constant when the net _______________ on the body is zero.

Question 48

When a planet moves closer to the Sun in an elliptical orbit, its rotational inertia

A) does not change because the mass of the planet is constant.
B) gets smaller because its distance from the Sun is smaller.
C) gets smaller because the lever arm is shorter.
D) gets larger because the angular momentum must be conserved.
E) gets larger because the planet has more angular acceleration.

Question 49

If an object has an angular acceleration larger than zero, its angular __________ must be changing with time.

Question 50

In principle, a first-grader could measurably move the Earth if

A) she pushed her hardest on the Earth.
B) she had a long enough lever.
C) she ran her fastest opposite the spin of the Earth.
D) she was at the North Pole and had a bicycle wheel spinning opposite the spin of Earth.

Question 51

If the net force on a body is zero the net torque _______________________ (is always, is not necessarily, cannot be) zero.

Question 52

Even a little first-grader can stay up on a bicycle if he can get his bicycle moving fast enough because

A) the angular momentum of the wheels wants to stay horizontal, due to conservation of angular momentum.
B) the first-grader's weight causes a torque too small to make the bicycle fall sideways when moving.
C) pedaling faster is easier once you are stable, and more pedaling increases net angular momentum.
D) All of these.

Question 53

A spinning wheel has an angular momentum that points toward the east. If an eastward force is applied to the edge of the wheel,

A) the angular momentum of the wheel will change direction but not magnitude.
B) the angular momentum will get larger.
C) the angular momentum will get smaller.
D) the angular momentum of the wheel will not change.

Question 54

A merry-go-round is set into motion with a child on board. The rotational speed of the merry-go-round _____________ as the child moves inward along a radius.