Deck 4: Probability and Probability Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/150
Play
Full screen (f)
Deck 4: Probability and Probability Models
1
If events A and B are independent, then P(A|B) is always equal to zero.
False
2
A subjective probability is a probability assessment that is based on experience, intuitive judgment, or expertise.
True
3
Events that have no sample space outcomes in common, and therefore cannot occur simultaneously, are referred to as independent events.
False
4
Bayes' Theorem is always based on two states of nature and three experimental outcomes.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
5
An event is a collection of sample space outcomes.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
6
A probability model is a mathematic representation of a random phenomenon.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
7
Two mutually exclusive events having positive probabilities are ________ dependent.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
8
If events A and B are mutually exclusive, then P(A|B) is always equal to zero.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
9
A manager has just received the expense checks for six of her employees. She randomly distributes the checks to the six employees. What is the probability that exactly five of them will receive the correct checks (checks with the correct names)?
A) 1
B) 1/2
C) 1/6
D) 0
E) 1/3
A) 1
B) 1/2
C) 1/6
D) 0
E) 1/3

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
10
Mutually exclusive events have a nonempty intersection.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
11
In which of the following are the two events A and B always independent?
A) A and B are mutually exclusive.
B) The probability of event A is influenced by the probability of event B.
C) The intersection of A and B is zero.
D) P(A|B) = P(B|A).
E) The probability of event A is not influenced by whether event B occurs, or P(A|B) = P(A).
A) A and B are mutually exclusive.
B) The probability of event A is influenced by the probability of event B.
C) The intersection of A and B is zero.
D) P(A|B) = P(B|A).
E) The probability of event A is not influenced by whether event B occurs, or P(A|B) = P(A).

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
12
There are two types of probability distributions: discrete and binomial.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
13
A ________ is a measure of the chance that an uncertain event will occur.
A) random experiment
B) sample space
C) probability
D) complement
E) population
A) random experiment
B) sample space
C) probability
D) complement
E) population

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
14
The probability of an event is the sum of the probabilities of the sample space outcomes that correspond to the event.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
15
In any probability situation, either an event or its complement must occur.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
16
Two events are independent if the probability of one event is influenced by whether or not the other event occurs.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
17
If events A and B are mutually exclusive, then P(A∩B) is always equal to zero.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
18
A random variable is a numerical value that is determined by the outcome of an experiment.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
19
Bayes' Theorem uses prior probabilities with additional information to compute posterior probabilities.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
20
The method of assigning probabilities when all outcomes are equally likely to occur is called the classical method.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
21
The ________ of an event is a number that measures the likelihood that an event will occur when an experiment is carried out.
A) outcome
B) probability
C) intersection
D) observation
A) outcome
B) probability
C) intersection
D) observation

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
22
A(n) ________ probability is a probability assessment that is based on experience, intuitive judgment, or expertise.
A) experimental
B) relative frequency
C) objective
D) subjective
A) experimental
B) relative frequency
C) objective
D) subjective

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
23
Probabilities must be assigned to each sample space outcome so that the probabilities of all the sample space outcomes add up to ________.
A) 1
B) between 0 and 1
C) between −1 and 1
D) 0
A) 1
B) between 0 and 1
C) between −1 and 1
D) 0

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
24
The set of all possible outcomes for an experiment is called a(n) ________.
A) sample space
B) event
C) experiment
D) probability
A) sample space
B) event
C) experiment
D) probability

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
25
If two events are independent, we can ________ their probabilities to determine the intersection probability.
A) divide
B) add
C) multiply
D) subtract
A) divide
B) add
C) multiply
D) subtract

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
26
A ________ is the probability that one event will occur given that we know that another event already has occurred.
A) sample space outcome
B) subjective probability
C) complement of events
D) long-run relative frequency
E) conditional probability
A) sample space outcome
B) subjective probability
C) complement of events
D) long-run relative frequency
E) conditional probability

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
27
If events A and B are independent, then the probability of simultaneous occurrence of event A and event B can be found with ________.
A) P(A)·P(B)
B) P(A)·P(B|A)
C) P(B)·P(A|B)
D) All of these choices are correct.
A) P(A)·P(B)
B) P(A)·P(B|A)
C) P(B)·P(A|B)
D) All of these choices are correct.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
28
Events that have no sample space outcomes in common, and therefore cannot occur simultaneously, are ________.
A) independent
B) mutually exclusive
C) intersections
D) unions
A) independent
B) mutually exclusive
C) intersections
D) unions

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
29
Probabilities must be assigned to sample space outcomes so that the probability assigned to each sample space outcome must be between ________, inclusive.
A) 0 and 100
B) −100 and 100
C) 0 and 1
D) −1 and 1
A) 0 and 100
B) −100 and 100
C) 0 and 1
D) −1 and 1

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
30
If events A and B are independent, then P(A|B) is equal to ________.
A) P(B)
B) P(A∩B)
C) P(A)
D) P(AUB)
A) P(B)
B) P(A∩B)
C) P(A)
D) P(AUB)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
31
If P(A) > 0 and P(B) > 0 and events A and B are independent, then ________.
A) P(A) = P(B)
B) P(A|B) = P(A)
C) P(A∩B) = 0
D) P(A∩B) = P(A) P(B∪A)
A) P(A) = P(B)
B) P(A|B) = P(A)
C) P(A∩B) = 0
D) P(A∩B) = P(A) P(B∪A)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
32
A probability may be interpreted as a long-run ________ frequency.
A) observational
B) relative
C) experimental
D) conditional
A) observational
B) relative
C) experimental
D) conditional

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
33
When the probability of one event is influenced by whether or not another event occurs, the events are said to be ________.
A) independent
B) dependent
C) mutually exclusive
D) experimental
A) independent
B) dependent
C) mutually exclusive
D) experimental

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
34
A(n) ________ is a collection of sample space outcomes.
A) experiment
B) event
C) set
D) probability
A) experiment
B) event
C) set
D) probability

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
35
A(n) ________ is the set of all of the distinct possible outcomes of an experiment.
A) sample space
B) union
C) intersection
D) observation
A) sample space
B) union
C) intersection
D) observation

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
36
P(AUB) = P(A) + P(B) − P(A∩B) represents the formula for the ________.
A) conditional probability
B) addition rule
C) addition rule for two mutually exclusive events
D) multiplication rule
A) conditional probability
B) addition rule
C) addition rule for two mutually exclusive events
D) multiplication rule

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
37
The simultaneous occurrence of events A and B is represented by the notation ________.
A) AUB
B) A|B
C) A∩B
D) B|A
A) AUB
B) A|B
C) A∩B
D) B|A

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
38
When the probability of one event is not influenced by whether or not another event occurs, the events are said to be ________.
A) independent
B) dependent
C) mutually exclusive
D) experimental
A) independent
B) dependent
C) mutually exclusive
D) experimental

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
39
A process of observation that has an uncertain outcome is referred to as a(n) ________.
A) probability
B) frequency
C) conditional probability
D) experiment
A) probability
B) frequency
C) conditional probability
D) experiment

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
40
The ________ of two events X and Y is another event that consists of the sample space outcomes belonging to either event X or event Y or both events X and Y.
A) complement
B) union
C) intersection
D) conditional probability
A) complement
B) union
C) intersection
D) conditional probability

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
41
What is the probability of rolling a value higher than eight with a pair of fair dice?
A) 6/36
B) 18/36
C) 10/36
D) 8/36
E) 12/36
A) 6/36
B) 18/36
C) 10/36
D) 8/36
E) 12/36

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
42
Determine whether these two events are mutually exclusive: someone born in the United States and a U.S. citizen.
A) mutually exclusive
B) not mutually exclusive
A) mutually exclusive
B) not mutually exclusive

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
43
Consider a standard deck of 52 playing cards, a randomly selected card from the deck, and the following events: R = red, B = black, A = ace, N = nine, D = diamond, and C = club. Are R and C mutually exclusive?
A) Yes, mutually exclusive.
B) No, not mutually exclusive.
A) Yes, mutually exclusive.
B) No, not mutually exclusive.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
44
Determine whether these two events are mutually exclusive: unmarried person and a person with an employed spouse.
A) mutually exclusive
B) not mutually exclusive
A) mutually exclusive
B) not mutually exclusive

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
45
The probability model describing an experiment consists of
A) sample space.
B) probabilities of the sample space outcomes.
C) sample space and probabilities of the sample space outcomes.
D) independent events.
E) random variables.
A) sample space.
B) probabilities of the sample space outcomes.
C) sample space and probabilities of the sample space outcomes.
D) independent events.
E) random variables.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
46
Consider a standard deck of 52 playing cards, a randomly selected card from the deck, and the following events: R = red, B = black, A = ace, N = nine, D = diamond, and C = club. Are R and A mutually exclusive?
A) Yes, mutually exclusive.
B) No, not mutually exclusive.
A) Yes, mutually exclusive.
B) No, not mutually exclusive.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
47
A lot contains 12 items, and 4 are defective. If three items are drawn at random from the lot, what is the probability they are not defective?
A) 0.3333
B) 0.2545
C) 0.5000
D) 0.2963
E) 0.0370
A) 0.3333
B) 0.2545
C) 0.5000
D) 0.2963
E) 0.0370

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
48
Consider a standard deck of 52 playing cards, a randomly selected card from the deck, and the following events: R = red, B = black, A = ace, N = nine, D = diamond, and C = club. Are A and N mutually exclusive?
A) Yes, mutually exclusive.
B) No, not mutually exclusive.
A) Yes, mutually exclusive.
B) No, not mutually exclusive.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
49
What is the probability of at least one tail in the toss of three fair coins?
A) 1/8
B) 4/8
C) 5/8
D) 7/8
E) 6/8
A) 1/8
B) 4/8
C) 5/8
D) 7/8
E) 6/8

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
50
What is the probability that a king appears in drawing a single card from a deck of 52 cards?
A) 4/13
B) 1/13
C) 1/52
D) 1/12
E) 2/13
A) 4/13
B) 1/13
C) 1/52
D) 1/12
E) 2/13

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
51
What is the probability of rolling a seven with a pair of fair dice?
A) 6/36
B) 3/36
C) 1/36
D) 8/36
E) 7/36
A) 6/36
B) 3/36
C) 1/36
D) 8/36
E) 7/36

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
52
Determine whether these two events are mutually exclusive: voter who favors gun control and an unregistered voter.
A) mutually exclusive
B) not mutually exclusive
A) mutually exclusive
B) not mutually exclusive

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
53
Determine whether these two events are mutually exclusive: consumer with an unlisted phone number and a consumer who does not drive.
A) mutually exclusive
B) not mutually exclusive
A) mutually exclusive
B) not mutually exclusive

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
54
Determine whether these two events are mutually exclusive: someone with three sisters and someone with four siblings.
A) mutually exclusive
B) not mutually exclusive
A) mutually exclusive
B) not mutually exclusive

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
55
The ________ of two events A and B is the event that consists of the sample space outcomes belonging to both event A and event B.
A) union
B) intersection
C) complement
D) mutual exclusivity
A) union
B) intersection
C) complement
D) mutual exclusivity

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
56
Consider a standard deck of 52 playing cards, a randomly selected card from the deck, and the following events: R = red, B = black, A = ace, N = nine, D = diamond, and C = club. Are D and C mutually exclusive?
A) Yes, mutually exclusive.
B) No, not mutually exclusive.
A) Yes, mutually exclusive.
B) No, not mutually exclusive.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
57
Consider a standard deck of 52 playing cards, a randomly selected card from the deck, and the following events: R = red, B = black, A = ace, N = nine, D = diamond, and C = club. Are N and C mutually exclusive?
A) Yes, mutually exclusive.
B) No, not mutually exclusive.
A) Yes, mutually exclusive.
B) No, not mutually exclusive.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
58
What is the probability that an even number appears on the toss of a die?
A) 0.5
B) 0.33
C) 0.25
D) 0.67
E) 1.00
A) 0.5
B) 0.33
C) 0.25
D) 0.67
E) 1.00

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
59
The ________ of event X consists of all sample space outcomes that do not correspond to the occurrence of event X.
A) independence
B) complement
C) conditional probability
D) dependence
A) independence
B) complement
C) conditional probability
D) dependence

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
60
If we consider the toss of four coins as an experiment, how many outcomes does the sample space consist of?
A) 8
B) 4
C) 16
D) 32
E) 2
A) 8
B) 4
C) 16
D) 32
E) 2

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
61
Container 1 has 8 items, 3 of which are defective. Container 2 has 5 items, 2 of which are defective. If one item is drawn from each container, what is the probability that both items are not defective?
A) 0.3750
B) 0.3846
C) 0.1500
D) 0.6154
E) 0.2000
A) 0.3750
B) 0.3846
C) 0.1500
D) 0.6154
E) 0.2000

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
62
A machine is made up of 3 components: an upper part, a middle part, and a lower part. The machine is then assembled. 5 percent of the upper parts are defective, 4 percent of the middle parts are defective, and 1 percent of the lower parts are defective. What is the probability that a machine is not defective?
A) 0.1000
B) 0.9029
C) 0.8000
D) 0.0002
E) 0.7209
A) 0.1000
B) 0.9029
C) 0.8000
D) 0.0002
E) 0.7209

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
63
A card is drawn from a standard deck. What is the probability the card is an ace, given that it is a club?
A) 1/52
B) 1/13
C) 4/13
D) 1/4
A) 1/52
B) 1/13
C) 4/13
D) 1/4

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
64
A group has 12 men and 4 women. If 3 people are selected at random from the group, what is the probability that they are all men?
A) 0.4219
B) 0.5143
C) 0.3929
D) 0.0156
E) 0.0045
A) 0.4219
B) 0.5143
C) 0.3929
D) 0.0156
E) 0.0045

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
65
A pair of dice is thrown. What is the probability that one of the faces is a 3, given that the sum of the two faces is 9?
A) 1/3
B) 1/36
C) 1/6
D) 1/2
E) 1/4
A) 1/3
B) 1/36
C) 1/6
D) 1/2
E) 1/4

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
66
A coin is tossed 6 times. What is the probability that at least one head occurs?
A) 63/64
B) 1/64
C) 1/36
D) 5/6
E) 1/2
A) 63/64
B) 1/64
C) 1/36
D) 5/6
E) 1/2

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
67
A card is drawn from a standard deck. Given that a face card is drawn, what is the probability it will be a king?
A) 1/3
B) 1/13
C) 4/13
D) 1/12
E) 1/4
A) 1/3
B) 1/13
C) 4/13
D) 1/12
E) 1/4

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
68
Container 1 has 8 items, 3 of which are defective. Container 2 has 5 items, 2 of which are defective. If one item is drawn from each container, what is the probability that the item from Container 1 is defective and the item from Container 2 is not defective?
A) 0.3846
B) 0.2250
C) 0.3750
D) 0.6154
E) 0.1500
A) 0.3846
B) 0.2250
C) 0.3750
D) 0.6154
E) 0.1500

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
69
At a college, 70 percent of the students are women, and 50 percent of the students receive a grade of C. 25 percent of the students are neither female nor C students. Use this contingency table. 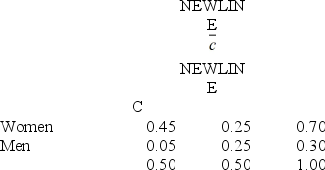 If a student is male, what is the probability he is a C student?
If a student is male, what is the probability he is a C student?
A) 0.05
B) 0.10
C) 0.30
D) 0.17
E) 0.50
 If a student is male, what is the probability he is a C student?
If a student is male, what is the probability he is a C student?A) 0.05
B) 0.10
C) 0.30
D) 0.17
E) 0.50

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
70
What is the probability of winning four games in a row, if the probability of winning each game individually is 1/2?
A) 1/4
B) 1/8
C) 1/2
D) 3/16
E) 1/16
A) 1/4
B) 1/8
C) 1/2
D) 3/16
E) 1/16

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
71
At a college, 70 percent of the students are women, and 50 percent of the students receive a grade of C. 25 percent of the students are neither female nor C students. Use this contingency table. 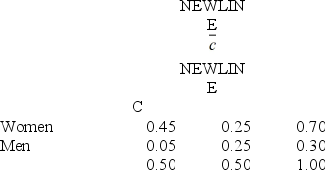 What is the probability that a student is female and a C student?
What is the probability that a student is female and a C student?
A) .45
B) .50
C) .70
D) .25
E) .05
 What is the probability that a student is female and a C student?
What is the probability that a student is female and a C student?A) .45
B) .50
C) .70
D) .25
E) .05

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
72
Given a standard deck of cards, what is the probability of drawing a face card, given that it is a red card?
A) 0.115
B) 0.500
C) 0.231
D) 0.462
E) 0.308
A) 0.115
B) 0.500
C) 0.231
D) 0.462
E) 0.308

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
73
Given the standard deck of cards, what is the probability of drawing a red card, given that it is a face card?
A) 0.500
B) 0.115
C) 0.231
D) 0.077
E) 0.308
A) 0.500
B) 0.115
C) 0.231
D) 0.077
E) 0.308

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
74
A machine is produced by a sequence of operations. On average, one out of every 1000 machines produced is defective. What is the probability that two machines selected at random are both nondefective?
A) 0.000999
B) 0.001
C) 0.002
D) 0.998
E) 0.500
A) 0.000999
B) 0.001
C) 0.002
D) 0.998
E) 0.500

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
75
Container 1 has 8 items, 3 of which are defective. Container 2 has 5 items, 2 of which are defective. If one item is drawn from each container, what is the probability that only one of the items is defective?
A) 0.2250
B) 0.6250
C) 0.2500
D) 0.4750
E) 0.1500
A) 0.2250
B) 0.6250
C) 0.2500
D) 0.4750
E) 0.1500

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
76
A family has two children. What is the probability that both are girls, given that at least one is a girl?
A) 1/8
B) 1/4
C) 1/2
D) 1/3
E) 1/6
A) 1/8
B) 1/4
C) 1/2
D) 1/3
E) 1/6

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
77
At a college, 70 percent of the students are women, and 50 percent of the students receive a grade of C. 25 percent of the students are neither female nor C students. Construct a contingency table.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
78
At a college, 70 percent of the students are women, and 50 percent of the students receive a grade of C. 25 percent of the students are neither female nor C students. Use this contingency table. 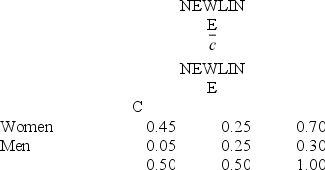 What is the probability that a student is male and not a C student?
What is the probability that a student is male and not a C student?
A) .45
B) .50
C) .70
D) .25
E) .05
 What is the probability that a student is male and not a C student?
What is the probability that a student is male and not a C student?A) .45
B) .50
C) .70
D) .25
E) .05

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
79
A person is dealt 5 cards from a deck of 52 cards. What is the probability they are all clubs?
A) 0.2500
B) 0.0962
C) 0.0769
D) 0.0010
E) 0.0005
A) 0.2500
B) 0.0962
C) 0.0769
D) 0.0010
E) 0.0005

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
80
Independently, a coin is tossed, a card is drawn from a deck, and a die is thrown. What is the probability of observing a head on the coin, an ace on the card, and a five on the die?
A) 0.0064
B) 0.1000
C) 0.7436
D) 0.0096
E) 0.5000
A) 0.0064
B) 0.1000
C) 0.7436
D) 0.0096
E) 0.5000

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck



