Deck 7: Multivariate Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/30
Play
Full screen (f)
Deck 7: Multivariate Models
1
What is the appropriate Box-Pierce test statistic?
A) 4.78
B) 47.83
C) 59.05
D) 5.91
A) 4.78
B) 47.83
C) 59.05
D) 5.91
47.83
2
Consider a series that follows an MA(1) with zero mean and a moving average coefficient of 0.4. What is the value of the autocorrelation function at lag 1?
A) 0.4
B) 1
C) 0.34
D) It is not possible to determine the value of the autocovariances without knowing the disturbance variance.
A) 0.4
B) 1
C) 0.34
D) It is not possible to determine the value of the autocovariances without knowing the disturbance variance.
0.34
3
Which of the following statements are true?
(I) An MA(q) can be expressed as an AR(infinity) if it is invertible
(ii) An AR(p) can be written as an MA(infinity) if it is stationary
(iii) The (unconditional) mean of an ARMA process will depend only on the intercept and on the AR coefficients and not on the MA coefficients
(iv) A random walk series will have zero pacf except at lag 1
A) (ii) and (iv) only
B) (i) and (iii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv).
(I) An MA(q) can be expressed as an AR(infinity) if it is invertible
(ii) An AR(p) can be written as an MA(infinity) if it is stationary
(iii) The (unconditional) mean of an ARMA process will depend only on the intercept and on the AR coefficients and not on the MA coefficients
(iv) A random walk series will have zero pacf except at lag 1
A) (ii) and (iv) only
B) (i) and (iii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv).
(i), (ii), (iii), and (iv).
4
Which of these is not a consequence of working with non-stationarity variables?
A) Shocks will be persistent
B) Unjustifiably high R2
C) The standard assumptions for asymptotic analysis will be invalid
D) It leads to data mining
A) Shocks will be persistent
B) Unjustifiably high R2
C) The standard assumptions for asymptotic analysis will be invalid
D) It leads to data mining

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
5
A process, xt, which has a constant mean and variance, and zero autocovariance for all non-zero lags is best described as
A) A white noise process
B) A covariance stationary process
C) An autocorrelated process
D) A moving average process
A) A white noise process
B) A covariance stationary process
C) An autocorrelated process
D) A moving average process

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
6
Which autocorrelation coefficients are significantly different from zero at the 5% level?
A) The first and fifth autocorrelation coefficient
B) The first, second, third and fifth autocorrelation coefficient
C) The first, third and fifth autocorrelation coefficient
D) The second and fourth autocorrelation coefficient
A) The first and fifth autocorrelation coefficient
B) The first, second, third and fifth autocorrelation coefficient
C) The first, third and fifth autocorrelation coefficient
D) The second and fourth autocorrelation coefficient

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
7
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
Consider the following AR(2) model. What is the optimal 2-step ahead forecast for y if all information available is up to and including time t, if the values of y at time t, t-1 and t-2 are -0.3, 0.4 and -0.1 respectively, and the value of u at time t-1 is 0.3? yt = -0.1 + 0.75yt-1 - 0.125yt-2 + ut
A) -0.1
B) 0.27
C) -0.34
D) 0.30
Consider the following AR(2) model. What is the optimal 2-step ahead forecast for y if all information available is up to and including time t, if the values of y at time t, t-1 and t-2 are -0.3, 0.4 and -0.1 respectively, and the value of u at time t-1 is 0.3? yt = -0.1 + 0.75yt-1 - 0.125yt-2 + ut
A) -0.1
B) 0.27
C) -0.34
D) 0.30

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the following model estimated for a time series yt = 0.3 + 0.5 yt-1 - 0.4 t-1 + t
Where t is a zero mean error process.
What is the (unconditional) mean of the series, yt ?
A) 0.6
B) 0.3
C) 0.0
D) 0.4
Where t is a zero mean error process.
What is the (unconditional) mean of the series, yt ?
A) 0.6
B) 0.3
C) 0.0
D) 0.4

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the following MA(3) process., yt = 0.1 + 0.4ut-1 + 0.2ut-2 - 0.1ut-3 + ut
What is the optimal forecast for yt, 3 steps into the future (i.e. for time t+2 if all information until time t-1 is available), if you have the following data?
Ut-1 = 0.3; ut-2 = -0.6; ut-3 = -0.3
A) 0.4
B) 0.0
C) 0.07
D) -0.1
What is the optimal forecast for yt, 3 steps into the future (i.e. for time t+2 if all information until time t-1 is available), if you have the following data?
Ut-1 = 0.3; ut-2 = -0.6; ut-3 = -0.3
A) 0.4
B) 0.0
C) 0.07
D) -0.1

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the following single exponential smoothing model: St = Xt + (1- ) St-1
You are given the following data:
=0)1, Xt=0.5,St-1=0.2 If we believe that the true DGP can be approximated by the exponential smoothing model, what would be an appropriate 2-step ahead forecast for X? (i.e. a forecast of Xt+2 made at time t)
If we believe that the true DGP can be approximated by the exponential smoothing model, what would be an appropriate 2-step ahead forecast for X? (i.e. a forecast of Xt+2 made at time t)
A) 0.2
B) 0.23
C) 0.5
D) There is insufficient information given in the question to form more than a one step ahead forecast.
You are given the following data:
=0)1, Xt=0.5,St-1=0.2
 If we believe that the true DGP can be approximated by the exponential smoothing model, what would be an appropriate 2-step ahead forecast for X? (i.e. a forecast of Xt+2 made at time t)
If we believe that the true DGP can be approximated by the exponential smoothing model, what would be an appropriate 2-step ahead forecast for X? (i.e. a forecast of Xt+2 made at time t)A) 0.2
B) 0.23
C) 0.5
D) There is insufficient information given in the question to form more than a one step ahead forecast.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
11
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
What is the optimal three-step ahead forecast from the AR(2) model given in question 14?
A) -0.1
B) 0.27
C) -0.34
D) -0.31
What is the optimal three-step ahead forecast from the AR(2) model given in question 14?
A) -0.1
B) 0.27
C) -0.34
D) -0.31

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following conditions must hold for the autoregressive part of an ARMA model to be stationary?
A) All roots of the characteristic equation must lie outside the unit circle
B) All roots of the characteristic equation must lie inside the unit circle
C) All roots must be smaller than unity
D) At least one of the roots must be bigger than one in absolute value.
A) All roots of the characteristic equation must lie outside the unit circle
B) All roots of the characteristic equation must lie inside the unit circle
C) All roots must be smaller than unity
D) At least one of the roots must be bigger than one in absolute value.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
13
If a series, yt, follows a random walk (with no drift), what is the optimal 1-step ahead forecast for y?
A) The current value of y.
B) Zero.
C) The historical unweighted average of y.
D) An exponentially weighted average of previous values of y.
A) The current value of y.
B) Zero.
C) The historical unweighted average of y.
D) An exponentially weighted average of previous values of y.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following statements are true concerning time-series forecasting?
(I) All time-series forecasting methods are essentially extrapolative.
(ii) Forecasting models are prone to perform poorly following a structural break in a series.
(iii) Forecasting accuracy often declines with prediction horizon.
(iv) The mean squared errors of forecasts are usually very highly correlated with the profitability of employing those forecasts in a trading strategy.
A) (i), (ii), (iii), and (iv)
B) (i), (ii) and (iii) only
C) (ii), (iii) only
D) (ii) and (iv) only
(I) All time-series forecasting methods are essentially extrapolative.
(ii) Forecasting models are prone to perform poorly following a structural break in a series.
(iii) Forecasting accuracy often declines with prediction horizon.
(iv) The mean squared errors of forecasts are usually very highly correlated with the profitability of employing those forecasts in a trading strategy.
A) (i), (ii), (iii), and (iv)
B) (i), (ii) and (iii) only
C) (ii), (iii) only
D) (ii) and (iv) only

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
15
Three characteristics of a weakly stationary process are
(I)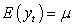 (II)
(II) 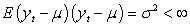 (III)
(III) 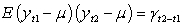
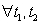 What do the mathematical expressions I, II and III imply?
What do the mathematical expressions I, II and III imply?
A) Constant variance, constant mean and constant autocovariance, respectively
B) Constant autocovariance structure, constant mean and constant variance, respectively
C) Constant mean, constant autocorrelation and constant autocovariance, respectively
D) Constant mean, constant variance and constant autocovariance structure, respectively
Use the following to answer questions 19 and 20. Suppose that you have estimated the first five autocorrelation coefficients using a series of length 81 observations and found them to be
(I)
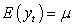 (II)
(II) 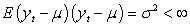 (III)
(III) 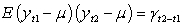
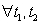 What do the mathematical expressions I, II and III imply?
What do the mathematical expressions I, II and III imply?A) Constant variance, constant mean and constant autocovariance, respectively
B) Constant autocovariance structure, constant mean and constant variance, respectively
C) Constant mean, constant autocorrelation and constant autocovariance, respectively
D) Constant mean, constant variance and constant autocovariance structure, respectively
Use the following to answer questions 19 and 20. Suppose that you have estimated the first five autocorrelation coefficients using a series of length 81 observations and found them to be


Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the following picture and suggest the model from the following list that best characterises the process: 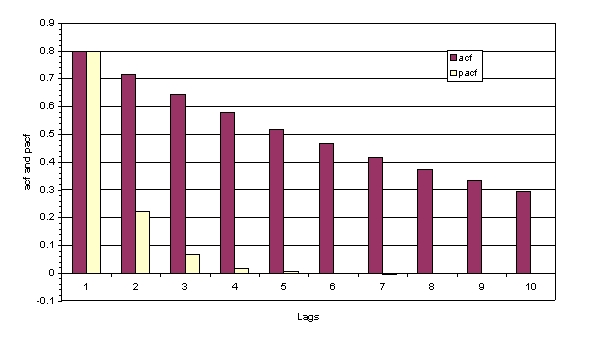
A) An AR(1)
B) An AR(2)
C) An ARMA(1,1)
D) An MA(3)

A) An AR(1)
B) An AR(2)
C) An ARMA(1,1)
D) An MA(3)

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
17
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
Suppose you had to guess at the most likely value of a one hundred step-ahead forecast for the AR(2) model given in question 14 - what would your forecast be?
A) -0.1
B) 0.7
C) -0.27
D) 0.75
Suppose you had to guess at the most likely value of a one hundred step-ahead forecast for the AR(2) model given in question 14 - what would your forecast be?
A) -0.1
B) 0.7
C) -0.27
D) 0.75

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
18
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
Which of the following models can be estimated using ordinary least squares? (i) An AR(1)
(ii) An ARMA(2,0)
(iii) An MA(1)
(iv) An ARMA(1,1)
A) (i) only
B) (i) and (ii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv).
Which of the following models can be estimated using ordinary least squares? (i) An AR(1)
(ii) An ARMA(2,0)
(iii) An MA(1)
(iv) An ARMA(1,1)
A) (i) only
B) (i) and (ii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv).

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following sets of characteristics would usually best describe an autoregressive process of order 3 )?
A) A slowly decaying acf, and a pacf with 3 significant spikes
B) A slowly decaying pacf and an acf with 3 significant spikes
C) A slowly decaying acf and pacf
D) An acf and a pacf with 3 significant spikes
A) A slowly decaying acf, and a pacf with 3 significant spikes
B) A slowly decaying pacf and an acf with 3 significant spikes
C) A slowly decaying acf and pacf
D) An acf and a pacf with 3 significant spikes

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
20
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
If a series, y, is described as "mean-reverting", which model from the following list is likely to produce the best long-term forecasts for that series y?
A) A random walk
B) The long term mean of the series
C) A model from the ARMA family
D) A random walk with drift
If a series, y, is described as "mean-reverting", which model from the following list is likely to produce the best long-term forecasts for that series y?
A) A random walk
B) The long term mean of the series
C) A model from the ARMA family
D) A random walk with drift

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
21
Which of these is an appropriate way to determine the order of an ARMA model required to capture the dynamic features of a given data?
A) Graphically plotting the time series of the data
B) Determining the number of parameters that maximises the information criteria
C) Determining the number of parameters that minimises the information criteria
D) None of the above
A) Graphically plotting the time series of the data
B) Determining the number of parameters that maximises the information criteria
C) Determining the number of parameters that minimises the information criteria
D) None of the above

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
22
What type of a process is ? 
A) An autoregressive model
B) An autoregressive moving average model
C) An autoregressive integrated moving average model
D) A periodic lag model

A) An autoregressive model
B) An autoregressive moving average model
C) An autoregressive integrated moving average model
D) A periodic lag model

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
23
Use the following to answer questions
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
Based on the MAE and MSE forecast evaluation metrics, which of these statements are true?
A) Model A outperforms Model B at forecasting the house price index
B) Model A underperforms Model B at forecasting the house price index
C) Model A and Model B perform equally well at forecasting the house price index
D) We cannot tell which model does best
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
Based on the MAE and MSE forecast evaluation metrics, which of these statements are true?
A) Model A outperforms Model B at forecasting the house price index
B) Model A underperforms Model B at forecasting the house price index
C) Model A and Model B perform equally well at forecasting the house price index
D) We cannot tell which model does best

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
24
A rolling window forecasting framework is one where
A) The initial estimation date is fixed but additional observations are added one at a time to the estimation period
B) The length of the in-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation
C) The initial estimation date changes as additional observations are added one at a time to the estimation period
D) The length of the out-of-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation.
A) The initial estimation date is fixed but additional observations are added one at a time to the estimation period
B) The length of the in-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation
C) The initial estimation date changes as additional observations are added one at a time to the estimation period
D) The length of the out-of-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation.

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
25
A model where the current value of a variable depends upon only the values that the variable took in previous periods plus an error term is called
A) An autoregressive model
B) An autoregressive moving average model
C) An autoregressive integrated moving average model
D) A periodic lag model
A) An autoregressive model
B) An autoregressive moving average model
C) An autoregressive integrated moving average model
D) A periodic lag model

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
26
Is the following process stationary? 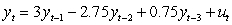
A) Yes
B) No
C) Partly stationary
D) Cannot say
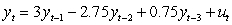
A) Yes
B) No
C) Partly stationary
D) Cannot say

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the following MA(2) process where the errors follow a standard normal distribution. What is the variance of? 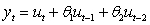
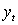
A)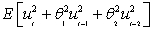
B)
C)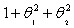
D) All of the above
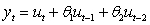
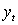
A)
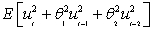
B)

C)
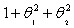
D) All of the above

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
28
Use the following to answer questions
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
What are the closest to the mean absolute errors from models A and B?
A) 0.58 and 0.98, respectively
B) 0.98 and 0.58, respectively
C) 0.45 and 1.95, respectively
D) 1.95 and 0.45, respectively
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
What are the closest to the mean absolute errors from models A and B?
A) 0.58 and 0.98, respectively
B) 0.98 and 0.58, respectively
C) 0.45 and 1.95, respectively
D) 1.95 and 0.45, respectively

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
29
Use the following to answer questions
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
What are the closest to the mean squared errors for model A and B's forecasts?
A) 0.58 and 0.98, respectively
B) 0.98 and 0.58, respectively
C) 0.45 and 1.95, respectively
D) 1.95 and 0.45, respectively
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
What are the closest to the mean squared errors for model A and B's forecasts?
A) 0.58 and 0.98, respectively
B) 0.98 and 0.58, respectively
C) 0.45 and 1.95, respectively
D) 1.95 and 0.45, respectively

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck
30
A recursive forecasting framework is one where
A) The initial estimation date is fixed but additional observations are added one at a time to the estimation period
B) The length of the in-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation
C) The initial estimation date changes as additional observations are added one at a time to the estimation period
D) The length of the out-of-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation
A) The initial estimation date is fixed but additional observations are added one at a time to the estimation period
B) The length of the in-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation
C) The initial estimation date changes as additional observations are added one at a time to the estimation period
D) The length of the out-of-sample period used to estimate the model is fixed so that the start date and end date successively increase by one observation

Unlock Deck
Unlock for access to all 30 flashcards in this deck.
Unlock Deck
k this deck



