Deck 2: Mathematical and Statistical Foundations
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/9
Play
Full screen (f)
Deck 2: Mathematical and Statistical Foundations
1
The unknown parameters of a Markov switching model are usually estimated using:
A) Maximum likelihood
B) Instrumental variables
C) Indirect least squares
D) Ordinary least squares
A) Maximum likelihood
B) Instrumental variables
C) Indirect least squares
D) Ordinary least squares
Maximum likelihood
2
Which of these equations is a self-exciting threshold autoregressive model?
A) if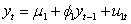
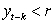 if
if 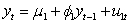

B) if
 if
if 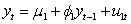
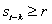
C) if
 if
if 
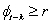
D) if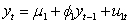
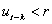 if
if 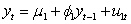
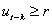
A) if
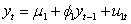
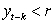 if
if 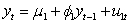

B) if

 if
if 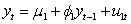
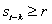
C) if

 if
if 
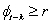
D) if
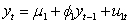
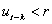 if
if 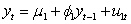
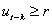
if 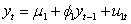
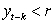 if
if 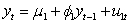

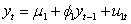
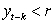 if
if 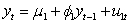

3
Threshold autoregressive and Markov switching models:
A) Allow us to potentially capture regime switches in a dependent variable
B) Forecast correlations of two distinct series
C) Maximise the threshold of autoregressive models
D) All of the above
A) Allow us to potentially capture regime switches in a dependent variable
B) Forecast correlations of two distinct series
C) Maximise the threshold of autoregressive models
D) All of the above
Allow us to potentially capture regime switches in a dependent variable
4
The key difference between threshold autoregressive and Markov switching models is that:
A) The latter can be estimated using ordinary least squares while the latter is estimated using indirect least squares estimation technique
B) Under the latter, the state variable is assumed to be known and observable, while it is latent under the former
C) Under the former, the state variable is assumed to be known and observable, while it is latent under the latter
D) None of the above
A) The latter can be estimated using ordinary least squares while the latter is estimated using indirect least squares estimation technique
B) Under the latter, the state variable is assumed to be known and observable, while it is latent under the former
C) Under the former, the state variable is assumed to be known and observable, while it is latent under the latter
D) None of the above

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
5
To check for seasonality (day-of-the-week effect) in stock returns of South Korea, Malaysia, the Philippines, Taiwan and Thailand, Brooks and Persand (2001) regress daily returns in each of these countries' stock market on five dummy variables D1 to D5 representing each day of the week i.e. D1 for Mondays, D2 for Tuesdays, D3 for Wednesdays, D4 for Thursdays and D5 for Fridays: 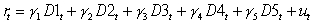 Their results were:
Their results were: 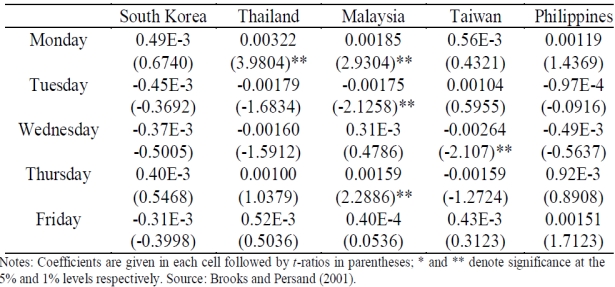
Which market(s) did not display any evidence of day-of-the-week effect?
A) Thailand, Malaysia and Taiwan
B) Philippines only
C) South Korea only
D) South Korea and Philippines
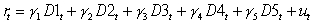 Their results were:
Their results were: 
Which market(s) did not display any evidence of day-of-the-week effect?
A) Thailand, Malaysia and Taiwan
B) Philippines only
C) South Korea only
D) South Korea and Philippines

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
6
A Markov process can be written mathematically as:
A)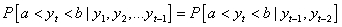
B)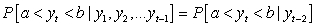
C)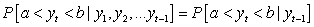
D)
A)
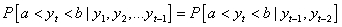
B)
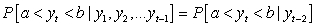
C)
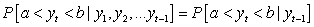
D)


Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
7
To compare the goodness of fit of Markov switching and threshold autoregressive models with linear models, one can compare the residual sums of squares of the two types of models using an F-test. Is the statement true?
A) Yes
B) No
C) If the autoregressive model is restricted
D) Cannot say without knowing the number of regimes in the regime switching models
A) Yes
B) No
C) If the autoregressive model is restricted
D) Cannot say without knowing the number of regimes in the regime switching models

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
8
Suppose that a researcher wishes to test for calendar (seasonal) effects using a dummy variables approach. Which of the following regressions could be used to examine this?
(I) A regression containing intercept dummies
(ii) A regression containing slope dummies
(iii) A regression containing intercept and slope dummies
(iv) A regression containing a dummy variable taking the value 1 for one observation and zero for all others
A) (ii) and (iv) only
B) (i) and (iii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv).
(I) A regression containing intercept dummies
(ii) A regression containing slope dummies
(iii) A regression containing intercept and slope dummies
(iv) A regression containing a dummy variable taking the value 1 for one observation and zero for all others
A) (ii) and (iv) only
B) (i) and (iii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv).

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck
9
If a series possesses the "Markov property", what would this imply?
(I) The series is path-dependent
(ii) All that is required to produce forecasts for the series is the current value of the series plus a transition probability matrix
(iii) The state-determining variable must be observable
(iv) The series can be classified as to whether it is in one regime or another regime, but it can only be in one regime at any one time
A) (ii) only
B) (i) and (ii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv)
(I) The series is path-dependent
(ii) All that is required to produce forecasts for the series is the current value of the series plus a transition probability matrix
(iii) The state-determining variable must be observable
(iv) The series can be classified as to whether it is in one regime or another regime, but it can only be in one regime at any one time
A) (ii) only
B) (i) and (ii) only
C) (i), (ii), and (iii) only
D) (i), (ii), (iii), and (iv)

Unlock Deck
Unlock for access to all 9 flashcards in this deck.
Unlock Deck
k this deck



