Deck 1: Introduction to Java Programming
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/8
Play
Full screen (f)
Deck 1: Introduction to Java Programming
1
Programming
Write a static method named sequenceSum that prints terms of the following mathematical sequence:
Your method should accept a real number as a parameter representing a limit, and should add and print terms of the sequence until the sum of terms meets or exceeds that limit. For example, if your method is passed 2.0, print terms until the sum of those terms is at ≥ 2.0. You should round your answer to 3 digits past the decimal point.
The following is the output from the call sequenceSum(2.0);
1 + 1/2 + 1/3 + 1/4 = 2.083
(Despite the fact that the terms keep getting smaller, the sequence can actually produce an arbitrarily large sum if enough terms are added.) If your method is passed a value less than 1.0, no output should be produced. You must match the output format shown exactly; note the spaces and pluses separating neighboring terms. Other sample calls:
Write a static method named sequenceSum that prints terms of the following mathematical sequence:
Your method should accept a real number as a parameter representing a limit, and should add and print terms of the sequence until the sum of terms meets or exceeds that limit. For example, if your method is passed 2.0, print terms until the sum of those terms is at ≥ 2.0. You should round your answer to 3 digits past the decimal point.
The following is the output from the call sequenceSum(2.0);
1 + 1/2 + 1/3 + 1/4 = 2.083
(Despite the fact that the terms keep getting smaller, the sequence can actually produce an arbitrarily large sum if enough terms are added.) If your method is passed a value less than 1.0, no output should be produced. You must match the output format shown exactly; note the spaces and pluses separating neighboring terms. Other sample calls:
(one solution shown)
public static void sequenceSum(double limit) {
if (limit >= 1) {
System.out.print("1");
int denomenator = 1;
double sum = 1.0;
while (sum < limit) {
denomenator++;
sum += 1.0 / denomenator;
System.out.print(" + 1/" + denomenator);
}
System.out.printf(" = %.3f\n", sum);
}
}
public static void sequenceSum(double limit) {
if (limit >= 1) {
System.out.print("1");
int denomenator = 1;
double sum = 1.0;
while (sum < limit) {
denomenator++;
sum += 1.0 / denomenator;
System.out.print(" + 1/" + denomenator);
}
System.out.printf(" = %.3f\n", sum);
}
}
2
Expressions
For each expression in the left-hand column, indicate its value in the right-hand column. Be sure to list a constant of appropriate type (e.g., 7.0 rather than 7 for a double, Strings in quotes, true/false for a boolean).
0||4==9 \%5| |1+1<1-1 & \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \end{array}">
For each expression in the left-hand column, indicate its value in the right-hand column. Be sure to list a constant of appropriate type (e.g., 7.0 rather than 7 for a double, Strings in quotes, true/false for a boolean).
0||4==9 \%5| |1+1<1-1 & \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \underline{ \text { }} \end{array}">
0||4==9 \%5| |1+1<1-1 & true \end{array}">
3
Parameter Mystery
At the bottom of the page, write the output produced by the following program.
public class ParameterMystery {
public static void main(String[] args) {
String x = "java";
String y = "tyler";
String z = "tv";
String rugby = "hamburger";
String java = "donnie";
hamburger(x, y, z);
hamburger(z, x, y);
hamburger("rugby", z, java);
hamburger(y, rugby, "x");
hamburger(y, y, "java");
}
public static void hamburger(String y, String z, String x) {
System.out.println(z + " and " + x + " like " + y);
}
}
At the bottom of the page, write the output produced by the following program.
public class ParameterMystery {
public static void main(String[] args) {
String x = "java";
String y = "tyler";
String z = "tv";
String rugby = "hamburger";
String java = "donnie";
hamburger(x, y, z);
hamburger(z, x, y);
hamburger("rugby", z, java);
hamburger(y, rugby, "x");
hamburger(y, y, "java");
}
public static void hamburger(String y, String z, String x) {
System.out.println(z + " and " + x + " like " + y);
}
}
tyler and tv like java
java and tyler like tv
tv and donnie like rugby
hamburger and x like tyler
tyler and java like tyler
java and tyler like tv
tv and donnie like rugby
hamburger and x like tyler
tyler and java like tyler
4
Programming
Write a static method named hasMidpoint that accepts three integers as parameters and returns true if one of the integers is the midpoint between the other two integers; that is, if one integer is exactly halfway between them. Your method should return false if no such midpoint relationship exists.
The integers could be passed in any order; the midpoint could be the 1st, 2nd, or 3rd. You must check all cases.
Write a static method named hasMidpoint that accepts three integers as parameters and returns true if one of the integers is the midpoint between the other two integers; that is, if one integer is exactly halfway between them. Your method should return false if no such midpoint relationship exists.
The integers could be passed in any order; the midpoint could be the 1st, 2nd, or 3rd. You must check all cases.

Unlock Deck
Unlock for access to all 8 flashcards in this deck.
Unlock Deck
k this deck
5
(Despite the fact that the terms keep getting smaller, the sequence can actually produce an arbitrarily large sum if enough terms are added.) If your method is passed a value less than 1.0, no output should be produced. You must match the output format shown exactly; note the spaces and pluses separating neighboring terms. Other sample calls:
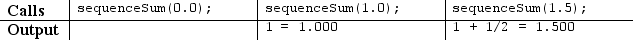
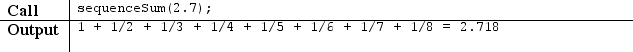
Programming
Write a static method named favoriteLetter that accepts two parameters: a Scanner for the console, and a favorite letter represented as a one-letter String. The method repeatedly prompts the user until two consecutive words are entered that start with that letter. The method then prints a message showing the last word typed.
You may assume that the user will type a single-word response to each prompt. Your code should be case-sensitive; for example, if the favorite letter is a, you should not stop prompting if the user types words that start with an A. For example, the following logs represent the output from two calls to your method: (User input is underlined.)
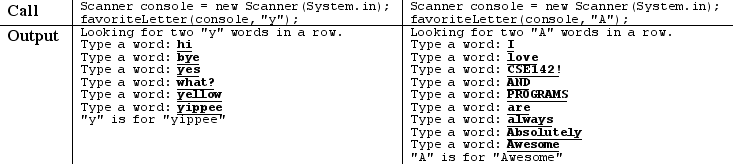
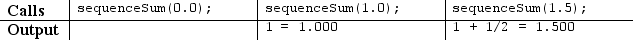
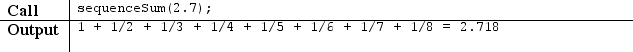
Programming
Write a static method named favoriteLetter that accepts two parameters: a Scanner for the console, and a favorite letter represented as a one-letter String. The method repeatedly prompts the user until two consecutive words are entered that start with that letter. The method then prints a message showing the last word typed.
You may assume that the user will type a single-word response to each prompt. Your code should be case-sensitive; for example, if the favorite letter is a, you should not stop prompting if the user types words that start with an A. For example, the following logs represent the output from two calls to your method: (User input is underlined.)


Unlock Deck
Unlock for access to all 8 flashcards in this deck.
Unlock Deck
k this deck
6
If/Else Simulation
For each call of the method below, write the value that is returned:
public static int mystery(int a, int b) {
int c;
if (a > b) {
c = a;
} else if (b % a == 0) {
c = b;
} else {
c = b + (a - (b % a));
}
return c;
}
For each call of the method below, write the value that is returned:
public static int mystery(int a, int b) {
int c;
if (a > b) {
c = a;
} else if (b % a == 0) {
c = b;
} else {
c = b + (a - (b % a));
}
return c;
}

Unlock Deck
Unlock for access to all 8 flashcards in this deck.
Unlock Deck
k this deck
7
While Loop Simulation
For each call of the method below, write the output that is printed:
public static void mystery(int i, int j) {
while (i != 0 && j != 0) {
i = i / j;
j = (j - 1) / 2;
System.out.print(i + " " + j + " ");
}
System.out.println(i);
}
For each call of the method below, write the output that is printed:
public static void mystery(int i, int j) {
while (i != 0 && j != 0) {
i = i / j;
j = (j - 1) / 2;
System.out.print(i + " " + j + " ");
}
System.out.println(i);
}

Unlock Deck
Unlock for access to all 8 flashcards in this deck.
Unlock Deck
k this deck
8
Assertions
For the following method, identify each of the three assertions in the table below as being either ALWAYS true, NEVER true or SOMETIMES true / sometimes false at each labeled point in the code. (You may abbreviate these choices as A/N/S respectively.)
public static int mystery(int x) {
int y = 1;
int z = 0;
// Point A
while (y <= x) {
// Point B
y = y * 10;
z++;
// Point C
}
// Point D
z--;
// Point E
return z;
}
For the following method, identify each of the three assertions in the table below as being either ALWAYS true, NEVER true or SOMETIMES true / sometimes false at each labeled point in the code. (You may abbreviate these choices as A/N/S respectively.)
public static int mystery(int x) {
int y = 1;
int z = 0;
// Point A
while (y <= x) {
// Point B
y = y * 10;
z++;
// Point C
}
// Point D
z--;
// Point E
return z;
}

Unlock Deck
Unlock for access to all 8 flashcards in this deck.
Unlock Deck
k this deck



