Deck 11: Regression Analysis: Statistical Inference
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/82
Play
Full screen (f)
Deck 11: Regression Analysis: Statistical Inference
1
Which of the following is the relevant sampling distribution for regression coefficients?
A) normal distribution
B) t-distribution with n-1 degrees of freedom
C) t-distribution with n-1-k degrees of freedom
D) F-distribution with n-1-k degrees of freedom
A) normal distribution
B) t-distribution with n-1 degrees of freedom
C) t-distribution with n-1-k degrees of freedom
D) F-distribution with n-1-k degrees of freedom
t-distribution with n-1-k degrees of freedom
2
Suppose you run a regression of a person's height on his/her right and left foot sizes, and you suspect that there may be multicollinearity between the foot sizes. What types of problems might you see if your suspicions are true?
A) "wrong" values for the coefficients for the left and right foot size
B) large p-values for the coefficients for the left and right foot size
C) small t-values for the coefficients for the left and right foot size
D) all of these choices
A) "wrong" values for the coefficients for the left and right foot size
B) large p-values for the coefficients for the left and right foot size
C) small t-values for the coefficients for the left and right foot size
D) all of these choices
all of these choices
3
The term autocorrelation refers to the observation that:
A) analyzed data refers to itself
B) sample is related too closely to the population
C) data are in a loop (values repeat themselves)
D) time series variables are usually related to their own past values
A) analyzed data refers to itself
B) sample is related too closely to the population
C) data are in a loop (values repeat themselves)
D) time series variables are usually related to their own past values
time series variables are usually related to their own past values
4
In regression analysis, the ANOVA table analyzes:
A) the variation of the response variable Y
B) the variation of the explanatory variable X
C) the total variation of all variables
D) all of these choices
A) the variation of the response variable Y
B) the variation of the explanatory variable X
C) the total variation of all variables
D) all of these choices

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
5
The value k in the number of degrees of freedom, n-k-1, for the sampling distribution of the regression coefficients represents the:
A) sample size
B) population size
C) number of coefficients in the regression equation, including the constant
D) number of independent variables included in the equation
A) sample size
B) population size
C) number of coefficients in the regression equation, including the constant
D) number of independent variables included in the equation

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
6
In the standardized value 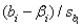 , the symbol
, the symbol 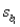 represents the:
represents the:
A) mean of
B) variance of
C) standard error of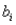
D) degrees of freedom of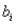
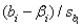 , the symbol
, the symbol 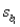 represents the:
represents the:A) mean of
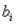
B) variance of
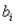
C) standard error of
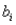
D) degrees of freedom of
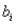

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
7
The appropriate hypothesis test for an ANOVA test is:
A)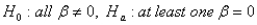
B)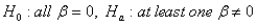
C)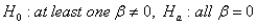
D)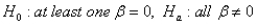
A)
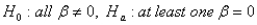
B)
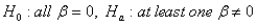
C)
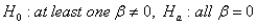
D)
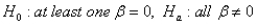

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
8
The appropriate hypothesis test for a regression coefficient is:
A)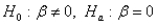
B)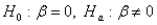
C)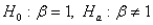
D) none of these choices
A)
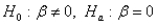
B)
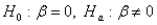
C)
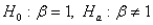
D) none of these choices

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
9
There is evidence that the regression equation provides little explanatory power when the F-ratio:
A) is large
B) equals the regression coefficient
C) is small
D) is the constant
A) is large
B) equals the regression coefficient
C) is small
D) is the constant

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
10
The ANOVA table splits the total variation into two parts. They are the:
A) acceptable and unacceptable variation
B) adequate and inadequate variation
C) resolved and unresolved variation
D) explained and unexplained variation
A) acceptable and unacceptable variation
B) adequate and inadequate variation
C) resolved and unresolved variation
D) explained and unexplained variation

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
11
Which definition best describes parsimony?
A) explaining the most with the least
B) explaining the least with the most
C) being able to explain all of the change in the response variable
D) being able to predict the value of the response variable far into the future
A) explaining the most with the least
B) explaining the least with the most
C) being able to explain all of the change in the response variable
D) being able to predict the value of the response variable far into the future

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
12
An error term represents the vertical distance from any point to the:
A) estimated regression line
B) population regression line
C) value of the Y's
D) mean value of the X's
A) estimated regression line
B) population regression line
C) value of the Y's
D) mean value of the X's

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
13
A scatterplot that exhibits a "fan" shape (the variation of Y increases as X increases) is an example of:
A) homoscedasticity
B) heteroscedasticity
C) autocorrelation
D) multicollinearity
A) homoscedasticity
B) heteroscedasticity
C) autocorrelation
D) multicollinearity

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
14
In regression analysis, multicollinearity refers to the:
A) response variables being highly correlated
B) explanatory variables being highly correlated
C) response variable(s) and the explanatory variable(s) being highly correlated with one another
D) response variables being highly correlated over time
A) response variables being highly correlated
B) explanatory variables being highly correlated
C) response variable(s) and the explanatory variable(s) being highly correlated with one another
D) response variables being highly correlated over time

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following is not one of the assumptions of regression?
A) There is a population regression line that joins the SDs of all possible distributions of results.
B) The response variable is normally distributed.
C) The standard deviation of the response variable increases as the explanatory variables increase.
D) The errors are probabilistically independent.
A) There is a population regression line that joins the SDs of all possible distributions of results.
B) The response variable is normally distributed.
C) The standard deviation of the response variable increases as the explanatory variables increase.
D) The errors are probabilistically independent.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
16
Time series data often exhibits which of the following characteristics?
A) homoscedasticity
B) heteroscedasticity
C) autocorrelation
D) multicollinearity
A) homoscedasticity
B) heteroscedasticity
C) autocorrelation
D) multicollinearity

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
17
Another term for constant error variance is:
A) homoscedasticity
B) heteroscedasticity
C) autocorrelation
D) multicollinearity
A) homoscedasticity
B) heteroscedasticity
C) autocorrelation
D) multicollinearity

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
18
What is not one of the guidelines for including/excluding variables in a regression equation?
A) Look at the t-value and associated p-value.
B) Check whether the t-value is less than or greater than 1.0.
C) The variables are logically related to one another.
D) Use economic or physical theory to make the decision.
E) All of these choices are guidelines.
A) Look at the t-value and associated p-value.
B) Check whether the t-value is less than or greater than 1.0.
C) The variables are logically related to one another.
D) Use economic or physical theory to make the decision.
E) All of these choices are guidelines.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
19
Which statement is true regarding regression error, ε?
A) It is the same as a residual.
B) It can be calculated from the observed data.
C) It cannot be calculated from the observed data.
D) It is unbiased.
A) It is the same as a residual.
B) It can be calculated from the observed data.
C) It cannot be calculated from the observed data.
D) It is unbiased.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
20
The t-value for testing 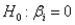 is calculated using which of the following equations?
is calculated using which of the following equations?
A) n - k - 1
B)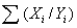
C)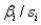
D)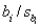
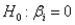 is calculated using which of the following equations?
is calculated using which of the following equations?A) n - k - 1
B)
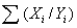
C)
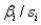
D)
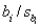

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
21
The objective typically used in the tree types of equation-building procedures is to:
A) find the equation with a small se
B) find the equation with a large R2
C) find the equation with a small se and a large R2
D) find the equation with the smallest F-ratio
A) find the equation with a small se
B) find the equation with a large R2
C) find the equation with a small se and a large R2
D) find the equation with the smallest F-ratio

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following would be considered a definition of an outlier?
A) an extreme value for one or more variables
B) a value whose residual is abnormally large in magnitude
C) values for individual explanatory variables that fall outside the general pattern of the other observations
D) all of these choices
A) an extreme value for one or more variables
B) a value whose residual is abnormally large in magnitude
C) values for individual explanatory variables that fall outside the general pattern of the other observations
D) all of these choices

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
23
Determining which variables to include in regression analysis by estimating a series of regression equations by successively adding or deleting variables according to prescribed rules is referred to as:
A) elimination regression
B) forward regression
C) backward regression
D) stepwise regression
A) elimination regression
B) forward regression
C) backward regression
D) stepwise regression

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
24
Which approach can be used to test for autocorrelation?
A) regression coefficient
B) correlation coefficient
C) Durbin-Watson statistic
D) F-test or t-test
A) regression coefficient
B) correlation coefficient
C) Durbin-Watson statistic
D) F-test or t-test

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
25
When the error variance is nonconstant, it is common to see the variation increases as the explanatory variable increases (you will see a "fan shape" in the scatterplot). There are two ways you can deal with this phenomenon. These are:
A) the weighted least squares and a logarithmic transformation
B) the partial F and a logarithmic transformation
C) the weighted least squares and the partial F
D) stepwise regression and the partial F
A) the weighted least squares and a logarithmic transformation
B) the partial F and a logarithmic transformation
C) the weighted least squares and the partial F
D) stepwise regression and the partial F

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose you forecast the values of all of the independent variables and insert them into a multiple regression equation and obtain a point prediction for the dependent variable. You could then use the standard error of the estimate to obtain an approximate:
A) confidence interval
B) prediction interval
C) hypothesis test
D) independence test
A) confidence interval
B) prediction interval
C) hypothesis test
D) independence test

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
27
In regression analysis, homoscedasticity refers to constant error variance.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
28
In regression analysis, extrapolation is performed when you:
A) attempt to predict beyond the limits of the sample
B) have to estimate some of the explanatory variable values
C) have to use a lag variable as an explanatory variable in the model
D) do not have observations for every period in the sample
A) attempt to predict beyond the limits of the sample
B) have to estimate some of the explanatory variable values
C) have to use a lag variable as an explanatory variable in the model
D) do not have observations for every period in the sample

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
29
A point that "tilts" the regression line toward it, is referred to as a(n):
A) magnetic point
B) influential point
C) extreme point
D) explanatory point
A) magnetic point
B) influential point
C) extreme point
D) explanatory point

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
30
The assumptions of regression are: 1) there is a population regression line, 2) the dependent variable is normally distributed, 3) the standard deviation of the response variable remains constant as the explanatory variables increase, and 4) the errors are probabilistically independent.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
31
If you can determine that the outlier is not really a member of the relevant population, then it is appropriate and probably best to:
A) average it
B) reduce it
C) delete it
D) leave it
A) average it
B) reduce it
C) delete it
D) leave it

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
32
When determining whether to include or exclude a variable in regression analysis, if the p-value associated with the variable's t-value is above some accepted significance value, such as 0.05, then the variable:
A) is a candidate for inclusion
B) is a candidate for exclusion
C) is redundant
D) does not fit the guidelines of parsimony
A) is a candidate for inclusion
B) is a candidate for exclusion
C) is redundant
D) does not fit the guidelines of parsimony

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
33
Multiple regression represents an improvement over simple regression because it allows any number of response variables to be included in the analysis.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
34
In a simple linear regression model, testing whether the slope 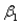 of the population regression line could be zero is the same as testing whether or not the linear relationship between the response variable Y and the explanatory variable X is significant.
of the population regression line could be zero is the same as testing whether or not the linear relationship between the response variable Y and the explanatory variable X is significant.
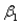 of the population regression line could be zero is the same as testing whether or not the linear relationship between the response variable Y and the explanatory variable X is significant.
of the population regression line could be zero is the same as testing whether or not the linear relationship between the response variable Y and the explanatory variable X is significant.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
35
Residuals separated by one period that are autocorrelated indicate:
A) simple autocorrelation
B) redundant autocorrelation
C) time 1 autocorrelation
D) lag 1 autocorrelation
A) simple autocorrelation
B) redundant autocorrelation
C) time 1 autocorrelation
D) lag 1 autocorrelation

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
36
A researcher can check whether the errors are normally distributed by using:
A) a t-test or an F-test
B) the Durbin-Watson statistic
C) a frequency distribution or the value of the regression coefficient
D) a histogram or a Q-Q plot
A) a t-test or an F-test
B) the Durbin-Watson statistic
C) a frequency distribution or the value of the regression coefficient
D) a histogram or a Q-Q plot

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
37
Forward regression:
A) begins with all potential explanatory variables in the equation and deletes them one at a time until further deletion would do more harm than good
B) adds and deletes variables until an optimal equation is achieved
C) begins with no explanatory variables in the equation and successively adds one at a time until no remaining variables make a significant contribution
D) randomly selects the optimal number of explanatory variables to be used
A) begins with all potential explanatory variables in the equation and deletes them one at a time until further deletion would do more harm than good
B) adds and deletes variables until an optimal equation is achieved
C) begins with no explanatory variables in the equation and successively adds one at a time until no remaining variables make a significant contribution
D) randomly selects the optimal number of explanatory variables to be used

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
38
In time series data, errors are often not probabilistically independent.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
39
Many statistical packages have three types of equation-building procedures. They are:
A) forward, linear, and non-linear
B) forward, backward, and stepwise
C) simple, complex, and stepwise
D) inclusion, exclusion, and linear
A) forward, linear, and non-linear
B) forward, backward, and stepwise
C) simple, complex, and stepwise
D) inclusion, exclusion, and linear

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
40
If exact multicollinearity exists, redundancy exists in the data.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
41
A forward procedure is a type of equation building procedure that begins with only one explanatory variable in the regression equation and successively adds one variable at a time until no remaining variables make a significant contribution.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
42
In multiple regression, the problem of multicollinearity affects the t-tests of the individual coefficients as well as the F-test in the analysis of variance for regression, since the F-test combines these t-tests into a single test.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
43
In multiple regressions, if the F-ratio is large, the explained variation is large relative to the unexplained variation.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
44
In simple linear regression, if the error variable 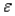 is normally distributed, the test statistic for testing
is normally distributed, the test statistic for testing 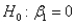 is t-distributed with n - 2 degrees of freedom.
is t-distributed with n - 2 degrees of freedom.
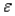 is normally distributed, the test statistic for testing
is normally distributed, the test statistic for testing 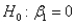 is t-distributed with n - 2 degrees of freedom.
is t-distributed with n - 2 degrees of freedom.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
45
When there is a group of explanatory variables that are in some sense logically related, all of them must be included in the regression equation.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
46
In a simple linear regression problem, if the standard error of estimate 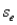 = 15 and n = 8, then the sum of squares for error, SSE, is 1,350.
= 15 and n = 8, then the sum of squares for error, SSE, is 1,350.
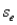 = 15 and n = 8, then the sum of squares for error, SSE, is 1,350.
= 15 and n = 8, then the sum of squares for error, SSE, is 1,350.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
47
The residuals are observations of the error variable 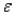 . Consequently, the minimized sum of squared deviations is called the sum of squared error, labeled SSE.
. Consequently, the minimized sum of squared deviations is called the sum of squared error, labeled SSE.
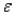 . Consequently, the minimized sum of squared deviations is called the sum of squared error, labeled SSE.
. Consequently, the minimized sum of squared deviations is called the sum of squared error, labeled SSE.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
48
Multicollinearity is a situation in which two or more of the explanatory variables are highly correlated with each other.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
49
In order to test the significance of a multiple regression model involving 4 explanatory variables and 40 observations, the numerator and denominator degrees of freedom for the critical value of F are 4 and 35, respectively.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
50
In multiple regression with k explanatory variables, the t-tests of the individual coefficients allows us to determine whether 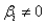 (for i = 1, 2, …., k), which tells us whether a linear relationship exists between
(for i = 1, 2, …., k), which tells us whether a linear relationship exists between 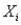 and Y.
and Y.
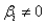 (for i = 1, 2, …., k), which tells us whether a linear relationship exists between
(for i = 1, 2, …., k), which tells us whether a linear relationship exists between 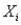 and Y.
and Y.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
51
In regression analysis, the unexplained part of the total variation in the response variable Y is referred to as the sum of squares due to regression, SSR.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
52
A multiple regression model involves 40 observations and 4 explanatory variables produces SST = 1000 and SSR = 804. The value of MSE is 5.6.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
53
In regression analysis, the total variation in the dependent variable Y, measured by 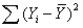 and referred to as SST, can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.
and referred to as SST, can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.
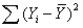 and referred to as SST, can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.
and referred to as SST, can be decomposed into two parts: the explained variation, measured by SSR, and the unexplained variation, measured by SSE.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
54
In testing the overall fit of a multiple regression model in which there are three explanatory variables, the null hypothesis is  .
.
 .
.
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
55
In multiple regression, if there is multicollinearity between independent variables, the t-tests of the individual coefficients may indicate that some variables are not linearly related to the dependent variable, when in fact, they are.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
56
In a multiple regression analysis involving 4 explanatory variables and 40 data points, the degrees of freedom associated with the sum of squared errors, SSE, is 35.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
57
In multiple regressions, if the F-ratio is small, the explained variation is small relative to the unexplained variation.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
58
Suppose that one equation has 3 explanatory variables and an F-ratio of 49. Another equation has 5 explanatory variables and an F-ratio of 38. The first equation will always be considered a better model.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
59
The value of the sum of squares due to regression, SSR, can never be larger than the value of the sum of squares total, SST.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
60
A backward procedure is a type of equation building procedure that begins with all potential explanatory variables in the regression equation and deletes them two at a time until further deletion would reduce the percentage of variation explained to a value less than 0.50.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
61
A confidence interval constructed around a point prediction from a regression model is called a prediction interval, because the actual point being estimated is not a population parameter.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
62
A carpet company, which sells and installs carpet, believes that there should be a relationship between the number of carpet installations that they will have to perform in a given month and the number of building permits that have been issued within the county where they are located. Below you will find a regression model that compares the relationship between the number of monthly carpet installations (Y) and the number of building permits that have been issued in a given month (X). The data represents monthly values for the past 10 months. 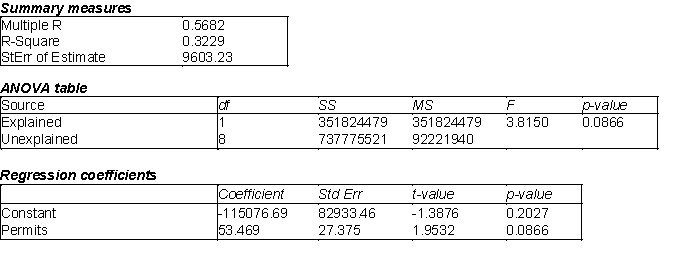
(A) Estimate the regression model. How well does this model fit the given data?
(B) Yes, there is a linear relationship between the number of carpet installations and the number of building permits issued at a = 0.10; The p-value = 0.0866 for the F-ratio. You can conclude that there is a significant linear relationship between these two variables.
(C) The Durbin-Watson statistic for this data was 1.2183. Given this information what would you conclude about the data?
(D) Given your answer in (C), would you recommend modifying the original regression model? If so, how would you modify it?

(A) Estimate the regression model. How well does this model fit the given data?
(B) Yes, there is a linear relationship between the number of carpet installations and the number of building permits issued at a = 0.10; The p-value = 0.0866 for the F-ratio. You can conclude that there is a significant linear relationship between these two variables.
(C) The Durbin-Watson statistic for this data was 1.2183. Given this information what would you conclude about the data?
(D) Given your answer in (C), would you recommend modifying the original regression model? If so, how would you modify it?

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
63
Many companies manufacture products that are at least partially produced using chemicals (for example, paint). In many cases, the quality of the finished product is a function of the temperature and pressure at which the chemical reactions take place. Suppose that a particular manufacturer in Texas wants to model the quality (Y) of a product as a function of the temperature 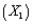 and the pressure
and the pressure 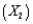 at which it is produced. The table below contains data obtained from a designed experiment involving these variables. Note that the assigned quality score can range from a minimum of 0 to a maximum of 100 for each manufactured product.
at which it is produced. The table below contains data obtained from a designed experiment involving these variables. Note that the assigned quality score can range from a minimum of 0 to a maximum of 100 for each manufactured product. 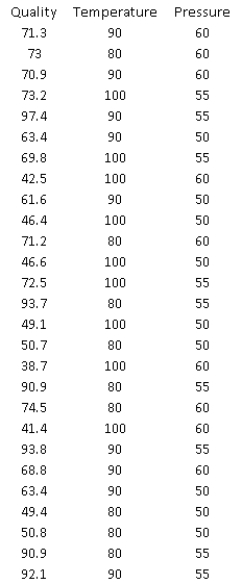
(A) Estimate a multiple regression model that includes the two given explanatory variables. Assess this set of explanatory variables with an F-test, and report a p-value.
(B) Identify and interpret the percentage of variance explained for the model in (A).
(C) Identify and interpret the percentage of variance explained for the model in (B).
(D) Which regression equation is the most appropriate one for modeling the quality of the given product? Bear in mind that a good statistical model is usually parsimonious.
 and the pressure
and the pressure  at which it is produced. The table below contains data obtained from a designed experiment involving these variables. Note that the assigned quality score can range from a minimum of 0 to a maximum of 100 for each manufactured product.
at which it is produced. The table below contains data obtained from a designed experiment involving these variables. Note that the assigned quality score can range from a minimum of 0 to a maximum of 100 for each manufactured product. 
(A) Estimate a multiple regression model that includes the two given explanatory variables. Assess this set of explanatory variables with an F-test, and report a p-value.
(B) Identify and interpret the percentage of variance explained for the model in (A).
(C) Identify and interpret the percentage of variance explained for the model in (B).
(D) Which regression equation is the most appropriate one for modeling the quality of the given product? Bear in mind that a good statistical model is usually parsimonious.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
64
Below you will find a scatterplot of data gathered by an online retail company. The company has been able to obtain the annual salaries of their customers and the amount that each of these customers spent on the company's site last year. Based on the scatterplot below, would you conclude that these data meet all four assumptions of regression? Explain your answer.
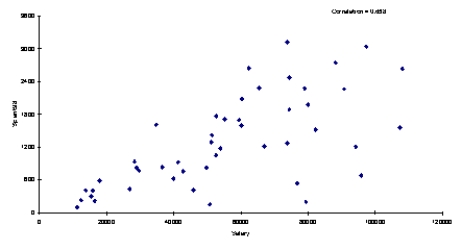


Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
65
The owner of a pizza restaurant chain would like to predict the sales of her recent specialty, a Mediterranean flatbread pizza. She has gathered data on monthly sales of the Mediterranean flatbread pizza at her restaurants. She has also gathered information related to the average price of flatbread pizzas, the monthly advertising expenditures, and the disposable income per household in the areas surrounding the restaurants. Below you will find output from the stepwise regression analysis. The p-value method was used with a cutoff of 0.05. 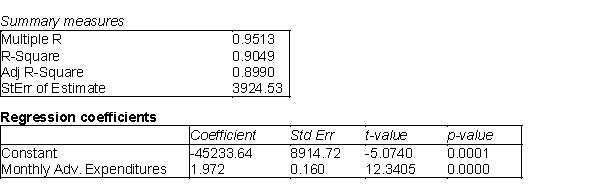
(A) Summarize the findings of the stepwise regression method using this cutoff value.
(B) When the cutoff value was increased to 0.10, the output below was the result. The table at top left represents the change when the disposable income variable is added to the model and the table at top right represents the average price variable being added. The regression model with both added variables is shown in the bottom table. Summarize the results for this model.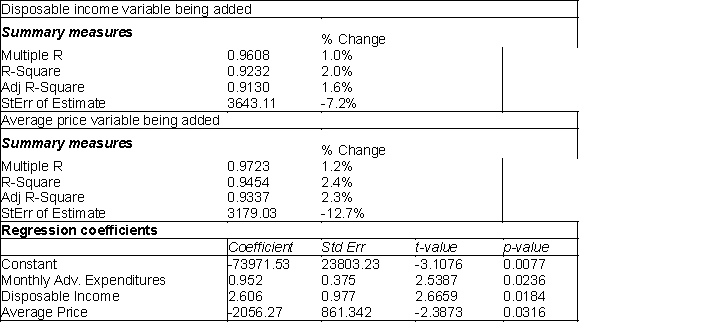 (C) Which model would you recommend using? Why?
(C) Which model would you recommend using? Why?

(A) Summarize the findings of the stepwise regression method using this cutoff value.
(B) When the cutoff value was increased to 0.10, the output below was the result. The table at top left represents the change when the disposable income variable is added to the model and the table at top right represents the average price variable being added. The regression model with both added variables is shown in the bottom table. Summarize the results for this model.
 (C) Which model would you recommend using? Why?
(C) Which model would you recommend using? Why?
Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
66
A new online auction site specializes in selling automotive parts for classic cars. The founder of the company believes that the price received for a particular item increases with its age (i.e., the age of the car on which the item can be used in years) and with the number of bidders. The Excel multiple regression output is shown below. 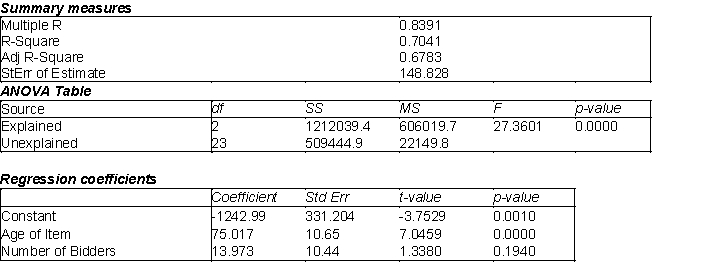
(A) Estimate a multiple regression model for the data.
(B) Which of the variables in this model have regression coefficients that are statistically different from 0 at the 5% significance level?
(C) Given your findings in (B), which variables, if any, would you choose to remove from the model estimated in (A)? Explain your decision.

(A) Estimate a multiple regression model for the data.
(B) Which of the variables in this model have regression coefficients that are statistically different from 0 at the 5% significance level?
(C) Given your findings in (B), which variables, if any, would you choose to remove from the model estimated in (A)? Explain your decision.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
67
The information below represents the relationship between the selling price (Y, in $1,000) of a home, the square footage of the home ( 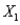 ), and the number of rooms in the home (
), and the number of rooms in the home ( 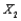 ). The data represents 60 homes sold in a particular area of East Lansing, Michigan and was analyzed using multiple linear regression and simple regression for each independent variable. The first two tables relate to the multiple regression analysis.
). The data represents 60 homes sold in a particular area of East Lansing, Michigan and was analyzed using multiple linear regression and simple regression for each independent variable. The first two tables relate to the multiple regression analysis. 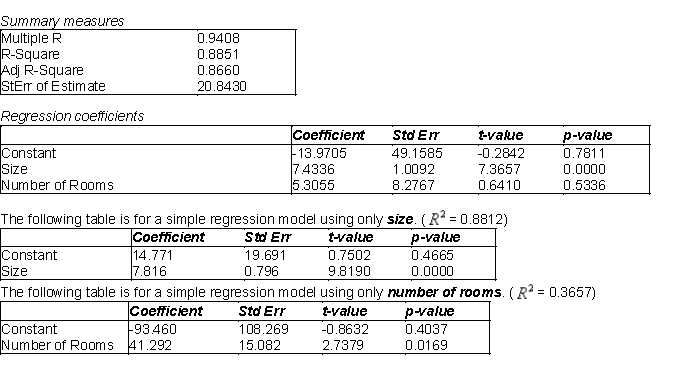
(A) Use the information related to the multiple regression model to determine whether each of the regression coefficients are statistically different from 0 at a 5% significance level. Summarize your findings.
(B) Test at the 5% significance level the relationship between Y and X in each of the simple linear regression models. How does this compare to your answer in (A)? Explain.
(C) Is there evidence of multicollinearity in this situation? Explain why or why not.
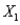 ), and the number of rooms in the home (
), and the number of rooms in the home ( 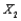 ). The data represents 60 homes sold in a particular area of East Lansing, Michigan and was analyzed using multiple linear regression and simple regression for each independent variable. The first two tables relate to the multiple regression analysis.
). The data represents 60 homes sold in a particular area of East Lansing, Michigan and was analyzed using multiple linear regression and simple regression for each independent variable. The first two tables relate to the multiple regression analysis. 
(A) Use the information related to the multiple regression model to determine whether each of the regression coefficients are statistically different from 0 at a 5% significance level. Summarize your findings.
(B) Test at the 5% significance level the relationship between Y and X in each of the simple linear regression models. How does this compare to your answer in (A)? Explain.
(C) Is there evidence of multicollinearity in this situation? Explain why or why not.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
68
One method of dealing with heteroscedasticity is to try a logarithmic transformation of the data.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
69
An Internet-based retail company that specializes in audio and visual equipment is interested in creating a model to determine the amount of money, in dollars, its customers will spend purchasing products from them in the coming year. In order to create a reliable model, this company has tracked a number of variables on its customers. Below you will find the Excel output related to several of these variables. This company has tried using the customer's annual salary for entire household 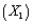 , the number of children in the household
, the number of children in the household 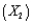 , and if the customer purchased merchandise from them in the previous year (
, and if the customer purchased merchandise from them in the previous year ( 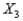 in 2015).
in 2015). 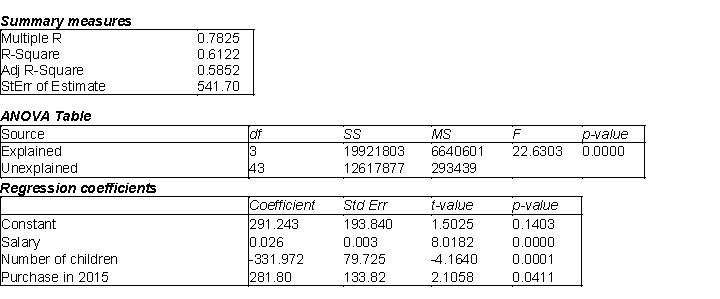
(A) Estimate the regression model. How well does this model fit the data?
(B) Is there a linear relationship between the explanatory variables and the dependent variable? Explain how you arrived at your answer at the 5% significance level.
(C) Use the estimated regression model to predict the amount of money a customer will spend if their annual salary is $45,000, they have 1 child and they were a customer that purchased merchandise in the previous year (2015).
(D) Find a 95% prediction interval for the point prediction calculated in (C). Use a t-multiple = 2.02.
(E) Find a 95% confidence interval for the amount of money spent by all customers sharing the characteristics described in (C). Use a t-multiple = 2.02.
(F) How do you explain the differences between the widths of the intervals in (D) and (E)?
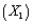 , the number of children in the household
, the number of children in the household 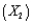 , and if the customer purchased merchandise from them in the previous year (
, and if the customer purchased merchandise from them in the previous year ( 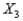 in 2015).
in 2015). 
(A) Estimate the regression model. How well does this model fit the data?
(B) Is there a linear relationship between the explanatory variables and the dependent variable? Explain how you arrived at your answer at the 5% significance level.
(C) Use the estimated regression model to predict the amount of money a customer will spend if their annual salary is $45,000, they have 1 child and they were a customer that purchased merchandise in the previous year (2015).
(D) Find a 95% prediction interval for the point prediction calculated in (C). Use a t-multiple = 2.02.
(E) Find a 95% confidence interval for the amount of money spent by all customers sharing the characteristics described in (C). Use a t-multiple = 2.02.
(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
70
The owner of a large chain of health spas has selected eight of her smaller clubs for a test in which she varies the size of the newspaper ad 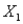 , and the amount of the initiation fee discount
, and the amount of the initiation fee discount 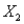 to see how this might affect the number of prospective members who visit each club during the following week. The results are shown in the table below:
to see how this might affect the number of prospective members who visit each club during the following week. The results are shown in the table below: 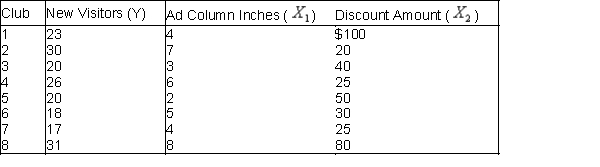 The results of a multiple regression analysis are below.
The results of a multiple regression analysis are below. 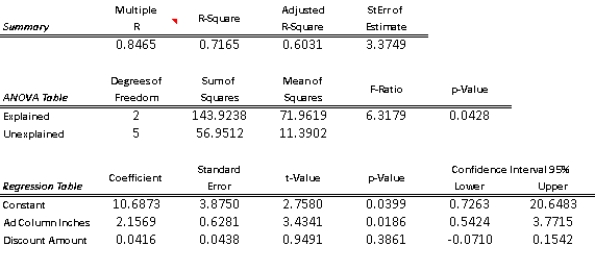
(A) Determine the least-squares multiple regression equation.
(B) Interpret the Y-intercept of the regression equation.
(C) Interpret the partial regression coefficients.
(D) What is the estimated number of new visitors to a club if the size of the ad is 6 column-inches and a $100 discount is offered?
(E) Determine the approximate 95% prediction interval for the number of new visitors to a given club when the ad is 5 column-inches and the discount is $80.
(F) What is the value for the percentage of variation explained, and exactly what does it indicate?
(G) At the 0.05 level, is the overall regression equation in (A) significant?
(H) Use the 0.05 level in concluding whether each partial regression coefficient differs significantly from zero.
(I Interpret the results of the preceding tests in (H) and (I) in the context of the two explanatory variables described in the problem.
(J) Construct a 95% confidence interval for each partial regression coefficient in the population regression equation.
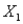 , and the amount of the initiation fee discount
, and the amount of the initiation fee discount 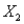 to see how this might affect the number of prospective members who visit each club during the following week. The results are shown in the table below:
to see how this might affect the number of prospective members who visit each club during the following week. The results are shown in the table below:  The results of a multiple regression analysis are below.
The results of a multiple regression analysis are below. 
(A) Determine the least-squares multiple regression equation.
(B) Interpret the Y-intercept of the regression equation.
(C) Interpret the partial regression coefficients.
(D) What is the estimated number of new visitors to a club if the size of the ad is 6 column-inches and a $100 discount is offered?
(E) Determine the approximate 95% prediction interval for the number of new visitors to a given club when the ad is 5 column-inches and the discount is $80.
(F) What is the value for the percentage of variation explained, and exactly what does it indicate?
(G) At the 0.05 level, is the overall regression equation in (A) significant?
(H) Use the 0.05 level in concluding whether each partial regression coefficient differs significantly from zero.
(I Interpret the results of the preceding tests in (H) and (I) in the context of the two explanatory variables described in the problem.
(J) Construct a 95% confidence interval for each partial regression coefficient in the population regression equation.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
71
A company that makes baseball caps would like to predict the sales of its main product, standard little league caps. The company has gathered data on monthly sales of caps at all of its retail stores, along with information related to the average retail price, which varies by location. Below you will find regression output comparing these two variables. 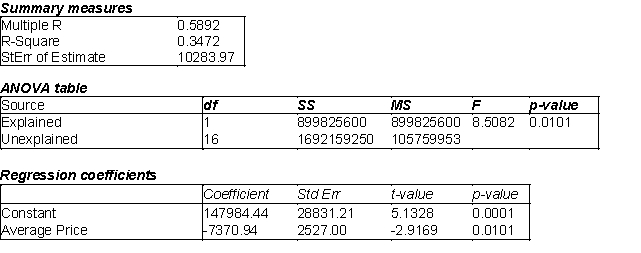
(A) Estimate the regression model. How well does this model fit the given data?
(B) Is there a linear relationship between X and Y at the 5% significance level? Explain how you arrived at your answer.
(C) Use the estimated regression model to predict the number of caps that will be sold during the next month if the average selling price is $10.
(D) Find a 95% prediction interval for the number of caps determined in (C). Use t- multiple = 2.
(E) Find a 95% confidence interval for the average number of caps sold given an average selling price of $10. Use a t-multiple = 2.
(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

(A) Estimate the regression model. How well does this model fit the given data?
(B) Is there a linear relationship between X and Y at the 5% significance level? Explain how you arrived at your answer.
(C) Use the estimated regression model to predict the number of caps that will be sold during the next month if the average selling price is $10.
(D) Find a 95% prediction interval for the number of caps determined in (C). Use t- multiple = 2.
(E) Find a 95% confidence interval for the average number of caps sold given an average selling price of $10. Use a t-multiple = 2.
(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
72
In order to estimate with 90% confidence a particular value of Y for a given value of X in a simple linear regression problem, a random sample of 20 observations is taken. The appropriate t-value that would be used is 1.734.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
73
The manager of a commuter rail transportation system is asked by his governing board to predict the demand for rides in the large city served by the transportation network. The system manager has collected data on variables thought to be related to the number of weekly riders on the city's rail system. The table shown below contains these data. 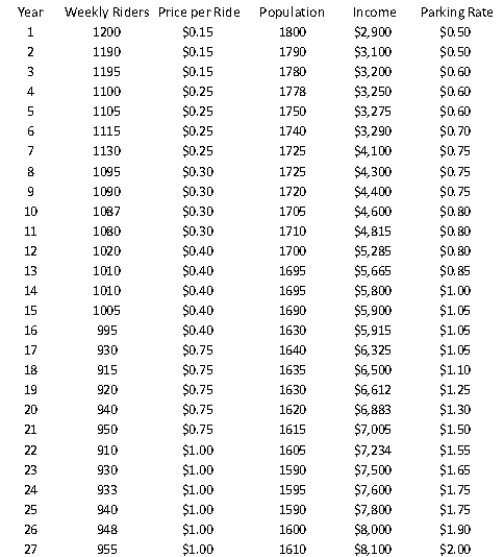 The variables "weekly riders" and "population" are measured in thousands, and the variables "price per ride", "income", and "parking rate" are measured in dollars.
The variables "weekly riders" and "population" are measured in thousands, and the variables "price per ride", "income", and "parking rate" are measured in dollars.
(A) Estimate a multiple regression model using all of the available explanatory variables.
(B) Conduct and interpret the result of an F- test on the given model. Employ a 5% level of significance in conducting this statistical hypothesis test.
(C) Is there evidence of autocorrelated residuals in this model? Explain why or why not.
 The variables "weekly riders" and "population" are measured in thousands, and the variables "price per ride", "income", and "parking rate" are measured in dollars.
The variables "weekly riders" and "population" are measured in thousands, and the variables "price per ride", "income", and "parking rate" are measured in dollars.(A) Estimate a multiple regression model using all of the available explanatory variables.
(B) Conduct and interpret the result of an F- test on the given model. Employ a 5% level of significance in conducting this statistical hypothesis test.
(C) Is there evidence of autocorrelated residuals in this model? Explain why or why not.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
74
Do you see any problems evident in the plot below of residuals versus fitted values from a multiple regression analysis? Explain your answer. 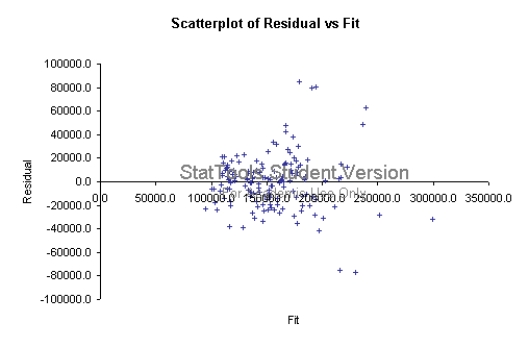


Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
75
A manufacturing firm wants to determine whether a relationship exists between the number of work-hours an employee misses per year (Y) and the employee's annual wages (X), to test the hypothesis that increased compensation induces better work attendance. The data provided in the table below are based on a random sample of 15 employees from this organization. 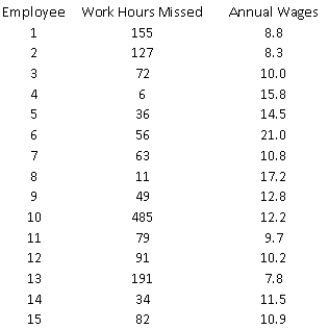
(A) Estimate a simple linear regression model using the sample data. How well does the estimated model fit the sample data?
(B) Perform an F-test for the existence of a linear relationship between Y and X. Use a 5% level of significance.
(C) Plot the fitted values versus residuals associated with the model. What does the plot indicate?
(D) How do you explain the results you have found in (A) through (C)?
(E) Suppose you learn that the 10th employee in the sample has been fired for missing an excessive number of work-hours during the past year. In light of this information, how would you proceed to estimate the relationship between the number of work-hours an employee misses per year and the employee's annual wages, using the available information? If you decide to revise your estimate of this regression equation, repeat (A) and (B)

(A) Estimate a simple linear regression model using the sample data. How well does the estimated model fit the sample data?
(B) Perform an F-test for the existence of a linear relationship between Y and X. Use a 5% level of significance.
(C) Plot the fitted values versus residuals associated with the model. What does the plot indicate?
(D) How do you explain the results you have found in (A) through (C)?
(E) Suppose you learn that the 10th employee in the sample has been fired for missing an excessive number of work-hours during the past year. In light of this information, how would you proceed to estimate the relationship between the number of work-hours an employee misses per year and the employee's annual wages, using the available information? If you decide to revise your estimate of this regression equation, repeat (A) and (B)

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
76
One of the potential characteristics of an outlier is that the value of the dependent variable is much larger or smaller than predicted by the regression line.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
77
One method of diagnosing heteroscedasticity is to plot the residuals against the predicted values of Y, then look for a change in the spread of the plotted values.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
78
A local truck rental company wants to use regression to predict the yearly maintenance expense (Y), in dollars, for a truck using the number of miles driven during the year 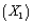 and the age of the truck in years
and the age of the truck in years 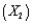 at the beginning of the year. To examine the relationship, the company has gathered the data on 15 trucks and regression analysis has been conducted. The regression output is presented below.
at the beginning of the year. To examine the relationship, the company has gathered the data on 15 trucks and regression analysis has been conducted. The regression output is presented below. 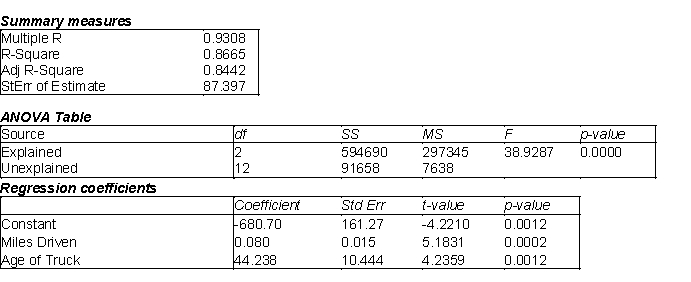
(A) Estimate the regression model. How well does this model fit the given data?
(B) Is there a linear relationship between the two explanatory variables and the dependent variable at the 5% significance level? Explain how you arrived at your answer.
(C) Use the estimated regression model to predict the annual maintenance expense of a truck that is driven 14,000 miles per year and is 5 years old.
(D) Find a 95% prediction interval for the maintenance expense determined in (C). Use a t-multiple = 2.
(E) Find a 95% confidence interval for the maintenance expense for all trucks sharing the characteristics provided in (C). Use a t-multiple = 2.
(F) How do you explain the differences between the widths of the intervals in (D) and (E)?
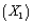 and the age of the truck in years
and the age of the truck in years 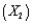 at the beginning of the year. To examine the relationship, the company has gathered the data on 15 trucks and regression analysis has been conducted. The regression output is presented below.
at the beginning of the year. To examine the relationship, the company has gathered the data on 15 trucks and regression analysis has been conducted. The regression output is presented below. 
(A) Estimate the regression model. How well does this model fit the given data?
(B) Is there a linear relationship between the two explanatory variables and the dependent variable at the 5% significance level? Explain how you arrived at your answer.
(C) Use the estimated regression model to predict the annual maintenance expense of a truck that is driven 14,000 miles per year and is 5 years old.
(D) Find a 95% prediction interval for the maintenance expense determined in (C). Use a t-multiple = 2.
(E) Find a 95% confidence interval for the maintenance expense for all trucks sharing the characteristics provided in (C). Use a t-multiple = 2.
(F) How do you explain the differences between the widths of the intervals in (D) and (E)?

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
79
The Durbin-Watson statistic can be used to test for autocorrelation.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck
80
Which of the following is not one of the assumptions of regression?
A) There is a population regression line.
B) The response variable is not normally distributed.
C) The response variable is normally distributed.
D) The errors are probabilistically independent.
A) There is a population regression line.
B) The response variable is not normally distributed.
C) The response variable is normally distributed.
D) The errors are probabilistically independent.

Unlock Deck
Unlock for access to all 82 flashcards in this deck.
Unlock Deck
k this deck



