Deck 5: Discrete Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/81
Play
Full screen (f)
Deck 5: Discrete Probability Distributions
1
The weight of an object is an example of
A) a continuous random variable.
B) a discrete random variable.
C) either a continuous or a discrete random variable, depending on the nature of the object.
D) either a continuous or a discrete random variable, depending on the unit of measurement.
A) a continuous random variable.
B) a discrete random variable.
C) either a continuous or a discrete random variable, depending on the nature of the object.
D) either a continuous or a discrete random variable, depending on the unit of measurement.
a continuous random variable.
2
A probability distribution showing the probability of x successes in n trials, where the probability of success does not change from trial to trial, is termed a
A) uniform probability distribution.
B) binomial probability distribution.
C) hypergeometric probability distribution.
D) normal probability distribution.
A) uniform probability distribution.
B) binomial probability distribution.
C) hypergeometric probability distribution.
D) normal probability distribution.
binomial probability distribution.
3
The Poisson probability distribution is a
A) continuous probability distribution.
B) discrete probability distribution.
C) uniform probability distribution.
D) normal probability distribution.
A) continuous probability distribution.
B) discrete probability distribution.
C) uniform probability distribution.
D) normal probability distribution.
discrete probability distribution.
4
Which of the following is a required condition for a discrete probability function?
A) f(x) = 0 for all values of x
B) f(x) 1 for all values of x
C) f(x) < 0 for all values of x
D) f(x) = 1 for all values of x
A) f(x) = 0 for all values of x
B) f(x) 1 for all values of x
C) f(x) < 0 for all values of x
D) f(x) = 1 for all values of x

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
5
The binomial probability distribution is used with
A) a continuous random variable.
B) a discrete random variable.
C) a uniform random variable.
D) an intermittent random variable.
A) a continuous random variable.
B) a discrete random variable.
C) a uniform random variable.
D) an intermittent random variable.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
6
A continuous random variable may assume
A) any numerical value in an interval or collection of intervals.
B) finite number of values in a collection of intervals.
C) an infinite sequence of values.
D) only the positive integer values in an interval.
A) any numerical value in an interval or collection of intervals.
B) finite number of values in a collection of intervals.
C) an infinite sequence of values.
D) only the positive integer values in an interval.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
7
A numerical description of the outcome of an experiment is called a
A) descriptive statistic.
B) probability function.
C) variance.
D) random variable.
A) descriptive statistic.
B) probability function.
C) variance.
D) random variable.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
8
The expected value of a discrete random variable
A) is the most likely or highest probability value for the random variable.
B) will always be one of the values x can take on, although it may not be the highest probability value for the random variable.
C) is the average value for the random variable over many repeats of the experiment.
D) is the value it is expected to assume in the next trial.
A) is the most likely or highest probability value for the random variable.
B) will always be one of the values x can take on, although it may not be the highest probability value for the random variable.
C) is the average value for the random variable over many repeats of the experiment.
D) is the value it is expected to assume in the next trial.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
9
The number of customers that enter a store during one day is an example of
A) a continuous random variable.
B) a discrete random variable.
C) either a continuous or a discrete random variable, depending on whether odd or even number of the customers enter.
D) either a continuous or a discrete random variable, depending on the gender of the customers.
A) a continuous random variable.
B) a discrete random variable.
C) either a continuous or a discrete random variable, depending on whether odd or even number of the customers enter.
D) either a continuous or a discrete random variable, depending on the gender of the customers.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
10
An experiment consists of determining the speed of automobiles on a highway by the use of radar equipment.The random variable in this experiment is a
A) discrete random variable.
B) continuous random variable.
C) mixed type random variable.
D) multivariate random variable.
A) discrete random variable.
B) continuous random variable.
C) mixed type random variable.
D) multivariate random variable.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
11
A weighted average of the values of a random variable, where the probability function provides weights, is known as
A) the probable value.
B) the median value.
C) the expected value.
D) the variance.
A) the probable value.
B) the median value.
C) the expected value.
D) the variance.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
12
In the textile industry, a manufacturer is interested in the number of blemishes or flaws occurring in each 100 feet of material.The probability distribution that has the greatest chance of applying to this situation is the
A) Normal distribution.
B) Binomial distribution.
C) Poisson distribution.
D) Uniform distribution.
A) Normal distribution.
B) Binomial distribution.
C) Poisson distribution.
D) Uniform distribution.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following is not a characteristic of an experiment where the binomial probability distribution is applicable?
A) The experiment has a sequence of n identical trials
B) Exactly two outcomes are possible on each trial
C) The trials are dependent
D) The probabilities of the outcomes do not change from one trial to another
A) The experiment has a sequence of n identical trials
B) Exactly two outcomes are possible on each trial
C) The trials are dependent
D) The probabilities of the outcomes do not change from one trial to another

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
14
Twenty percent of the students in a class of 100 are planning to go to graduate school.The standard deviation of this binomial distribution is
A) 20.
B) 16.
C) 4.
D) 2.
A) 20.
B) 16.
C) 4.
D) 2.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
15
Four percent of the customers of a mortgage company default on their payments.A sample of five customers is selected.What is the probability that exactly two customers in the sample will default on their payments?
A) 0.2592
B) 0.0142
C) 0.9588
D) 0.7408
A) 0.2592
B) 0.0142
C) 0.9588
D) 0.7408

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
16
A description of the distribution of the values of a random variable and their associated probabilities is called a
A) probability distribution.
B) empirical discrete distribution.
C) bivariate distribution.
D) table of binomial probability.
A) probability distribution.
B) empirical discrete distribution.
C) bivariate distribution.
D) table of binomial probability.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following is a required condition for a discrete probability function?
A) f(x) 0 for all values of x
B) f(x) = 1 for all values of x
C) f(x) = 0 for all values of x
D) f(x) 1 for all values of x
A) f(x) 0 for all values of x
B) f(x) = 1 for all values of x
C) f(x) = 0 for all values of x
D) f(x) 1 for all values of x

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following is a characteristic of an experiment where the binomial probability distribution is applicable?
A) The experiment has at least two possible outcomes
B) Exactly two outcomes are possible on each trial
C) The trials are dependent on each other
D) The probabilities of the outcomes changes from one trial
A) The experiment has at least two possible outcomes
B) Exactly two outcomes are possible on each trial
C) The trials are dependent on each other
D) The probabilities of the outcomes changes from one trial

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
19
A measure of the average value of a random variable is called a(n)
A) variance.
B) standard deviation.
C) expected value.
D) coefficient of variation.
A) variance.
B) standard deviation.
C) expected value.
D) coefficient of variation.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
20
The expected value of a random variable is
A) the value of the random variable that should be observed on the next repeat of the experiment
B) the value of the random variable that occurs most frequently
C) the square root of the variance
D) None of these alternatives is correct.
A) the value of the random variable that should be observed on the next repeat of the experiment
B) the value of the random variable that occurs most frequently
C) the square root of the variance
D) None of these alternatives is correct.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
21
A random variable that may take on any value in an interval or collection of intervals is known as a
A) continuous random variable.
B) discrete random variable.
C) mixed type random variable.
D) multivariate random variable.
A) continuous random variable.
B) discrete random variable.
C) mixed type random variable.
D) multivariate random variable.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
22
Assume that you have a binomial experiment with p = 0.4 and a sample size of 50.The variance of this distribution is
A) 20.
B) 12.
C) 3.46.
D) 144.
A) 20.
B) 12.
C) 3.46.
D) 144.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
23
The variance Var(x) for the binomial distribution is given by equation
A) np(n - 1).
B) np(1 - np).
C) n(1 - p).
D) np(1 - p).
A) np(n - 1).
B) np(1 - np).
C) n(1 - p).
D) np(1 - p).

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
24
The expected value for a binomial distribution is given by equation
A) (n - 1)(1 - p).
B) n(1 - p).
C) np.
D) (n - 1)p.
A) (n - 1)(1 - p).
B) n(1 - p).
C) np.
D) (n - 1)p.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
25
A production process produces 2% defective parts.A sample of five parts from the production process is selected.What is the probability that the sample contains exactly two defective parts?
A) 0.0004
B) 0.0038
C) 0.10
D) 0.02
A) 0.0004
B) 0.0038
C) 0.10
D) 0.02

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
26
The student body of a large university consists of 60% female students.A random sample of 8 students is selected.What is the probability that among the students in the sample at least 6 are male?
A) 0.0413
B) 0.0079
C) 0.0007
D) 0.0499
A) 0.0413
B) 0.0079
C) 0.0007
D) 0.0499

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
27
When dealing with the number of occurrences of an event over a specified interval of time or space, the appropriate probability distribution is a
A) Binomial distribution.
B) Poisson distribution.
C) Normal distribution.
D) Hypergeometric probability distribution.
A) Binomial distribution.
B) Poisson distribution.
C) Normal distribution.
D) Hypergeometric probability distribution.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
28
Roth is a computer-consulting firm.The number of new clients that they have obtained each month has ranged from 0 to 6.The number of new clients has the probability distribution that is shown below.
The standard deviation is
A) 1.431
B) 2.047
C) 3.05
D) 21
The standard deviation is
A) 1.431
B) 2.047
C) 3.05
D) 21

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
29
The Poisson probability distribution is used with
A) a continuous random variable.
B) a discrete random variable.
C) either a continuous or discrete random variable.
D) any random variable.
A) a continuous random variable.
B) a discrete random variable.
C) either a continuous or discrete random variable.
D) any random variable.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
30
In a binomial experiment
A) the probability does not change from trial to trial.
B) the probability changes from trial to trial.
C) the probability could change from trial to trial, depending on the situation under consideration.
D) the probability could change depending on the number of outcomes.
A) the probability does not change from trial to trial.
B) the probability changes from trial to trial.
C) the probability could change from trial to trial, depending on the situation under consideration.
D) the probability could change depending on the number of outcomes.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
31
In a binomial experiment the probability of success is 0.06.What is the probability of two successes in seven trials?
A) 0.0036
B) 0.0600
C) 0.0555
D) 0.2800
A) 0.0036
B) 0.0600
C) 0.0555
D) 0.2800

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
32
The following represents the probability distribution for the daily demand of computers at a local store. The probability of having a demand for at least two computers is
A) 0.7
B) 0.3
C) 0.4
D) 1.0
A) 0.7
B) 0.3
C) 0.4
D) 1.0

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
33
The student body of a large university consists of 60% female students.A random sample of 8 students is selected.What is the probability that among the students in the sample at least 7 are female?
A) 0.1064
B) 0.0896
C) 0.0168
D) 0.8936
A) 0.1064
B) 0.0896
C) 0.0168
D) 0.8936

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
34
The key difference between the binomial and hypergeometric distribution is that, with the hypergeometric distribution
A) the probability of success must be less than 0.5.
B) the probability of success changes from trial to trial.
C) the trials are independent of each other.
D) the random variable is continuous.
A) the probability of success must be less than 0.5.
B) the probability of success changes from trial to trial.
C) the trials are independent of each other.
D) the random variable is continuous.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
35
Random variable x has the probability function f(x) = X/6, for x = 1, 2 or 3 The expected value of x is
A) 0.333.
B) 0.500.
C) 2.000.
D) 2.333.
A) 0.333.
B) 0.500.
C) 2.000.
D) 2.333.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
36
The student body of a large university consists of 60% female students.A random sample of 8 students is selected.What is the probability that among the students in the sample exactly two are female?
A) 0.0896
B) 0.2936
C) 0.0413
D) 0.0007
A) 0.0896
B) 0.2936
C) 0.0413
D) 0.0007

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following is not a property of a binomial experiment?
A) The experiment consists of a sequence of n identical trials
B) Each outcome can be referred to as a success or a failure
C) The probabilities of the two outcomes can change from one trial to the next
D) The trials are independent
A) The experiment consists of a sequence of n identical trials
B) Each outcome can be referred to as a success or a failure
C) The probabilities of the two outcomes can change from one trial to the next
D) The trials are independent

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
38
The following represents the probability distribution for the daily demand of computers at a local store. The expected daily demand is
A) 1.0
B) 2.2
C) 2.0
D) 4.0
A) 1.0
B) 2.2
C) 2.0
D) 4.0

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
39
Roth is a computer-consulting firm.The number of new clients that they have obtained each month has ranged from 0 to 6.The number of new clients has the probability distribution that is shown below. The variance is
A) 1.431
B) 2.047
C) 3.05
D) 21
A) 1.431
B) 2.047
C) 3.05
D) 21

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
40
Roth is a computer-consulting firm.The number of new clients that they have obtained each month has ranged from 0 to 6.The number of new clients has the probability distribution that is shown below. The expected number of new clients per month is
A) 6
B) 0
C) 3.05
D) 21
A) 6
B) 0
C) 3.05
D) 21

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
41
The probability that Pete will catch fish when he goes fishing is .8.Pete is going to fish 3 days next week.Define the random variable x to be the number of days Pete catches fish.The variance of the number of days Pete will catch fish is
A) .16
B) .48
C) .8
D) 2.4
A) .16
B) .48
C) .8
D) 2.4

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
42
A sample of 2,500 people was asked how many cups of coffee they drink in the morning.You are given the following sample information. The variance of the number of cups of coffee is
A) .96
B) .9798
C) 1
D) 2.4
A) .96
B) .9798
C) 1
D) 2.4

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
43
The random variable x is the number of occurrences of an event over an interval of ten minutes.It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length.It is known that the mean number of occurrences in ten minutes is 5.3.The probability that there are less than 3 occurrences is
A) .0659
B) .0948
C) .1016
D) .1239
A) .0659
B) .0948
C) .1016
D) .1239

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
44
Oriental Reproductions, Inc.is a company that produces handmade carpets with oriental designs.The production records show that the monthly production has ranged from 1 to 5 carpets.The production levels and their respective probabilities are shown below. The standard deviation for the production is
A) 4.32
B) 3.74
C) 0.374
D) 0.612
A) 4.32
B) 3.74
C) 0.374
D) 0.612

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
45
The random variable x is the number of occurrences of an event over an interval of ten minutes.It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length.It is known that the mean number of occurrences in ten minutes is 5.3.The expected value of the random variable x is
A) 2.
B) 5.3.
C) 10.
D) 2.30.
A) 2.
B) 5.3.
C) 10.
D) 2.30.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
46
The probability that Pete will catch fish when he goes fishing is .8.Pete is going to fish 3 days next week.Define the random variable x to be the number of days Pete catches fish.The probability that Pete will catch fish on one day or less is
A) .008
B) .096
C) .104
D) .8
A) .008
B) .096
C) .104
D) .8

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
47
Forty percent of all registered voters in a national election are female.A random sample of 5 voters is selected. The probability that the sample contains 2 female voters is
A) 0.0778
B) 0.7780
C) 0.5000
D) 0.3456
A) 0.0778
B) 0.7780
C) 0.5000
D) 0.3456

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
48
The probability that Pete will catch fish when he goes fishing is .8.Pete is going to fish 3 days next week.Define the random variable x to be the number of days Pete catches fish.The probability that Pete will catch fish on exactly one day is
A) .008
B) .096
C) .104
D) .8
A) .008
B) .096
C) .104
D) .8

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
49
The probability distribution for the number of goals the Lions soccer team makes per game is given below.
What is the probability that in a given game the Lions will score at least 1 goal?
A) 0.20
B) 0.55
C) 1.0
D) 0.95
What is the probability that in a given game the Lions will score at least 1 goal?
A) 0.20
B) 0.55
C) 1.0
D) 0.95

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
50
The random variable x is the number of occurrences of an event over an interval of ten minutes.It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length.It is known that the mean number of occurrences in ten minutes is 5.3.Which of the following discrete probability distributions' properties are satisfied by random variable x?
A) Normal
B) Poisson
C) Binomial
D) Hypergeometric
A) Normal
B) Poisson
C) Binomial
D) Hypergeometric

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
51
The random variable x is the number of occurrences of an event over an interval of ten minutes.It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length.It is known that the mean number of occurrences in ten minutes is 5.3.The appropriate probability distribution for the random variable is
A) discrete.
B) continuous.
C) either discrete or continuous depending on how the interval is defined.
D) binomial.
A) discrete.
B) continuous.
C) either discrete or continuous depending on how the interval is defined.
D) binomial.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
52
Forty percent of all registered voters in a national election are female.A random sample of 5 voters is selected.The probability that there are no females in the sample is
A) 0.0778
B) 0.7780
C) 0.5000
D) 0.3456
A) 0.0778
B) 0.7780
C) 0.5000
D) 0.3456

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
53
The probability that Pete will catch fish when he goes fishing is .8.Pete is going to fish 3 days next week.Define the random variable x to be the number of days Pete catches fish.The expected number of days Pete will catch fish is
A) .6
B) .8
C) 2.4
D) 3
A) .6
B) .8
C) 2.4
D) 3

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
54
A sample of 2,500 people was asked how many cups of coffee they drink in the morning.You are given the following sample information. The expected number of cups of coffee is?
A) 1
B) 1.2
C) 1.5
D) 1.7
A) 1
B) 1.2
C) 1.5
D) 1.7

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
55
The probability distribution for the daily sales at Michael's Co.is given below.
The probability of having sales of no more than $60,000 is
A) 0.7
B) 0.2
C) 0.8
D) 0.5
The probability of having sales of no more than $60,000 is
A) 0.7
B) 0.2
C) 0.8
D) 0.5

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
56
Consider the probability distribution below. The variance of x equals
A) 9.165
B) 84
C) 85
D) 93.33
A) 9.165
B) 84
C) 85
D) 93.33

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
57
The random variable x is the number of occurrences of an event over an interval of ten minutes.It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length.It is known that the mean number of occurrences in ten minutes is 5.3.The probability that there are 8 occurrences in ten minutes is
A) .0241
B) .0771
C) .1126
D) .9107
A) .0241
B) .0771
C) .1126
D) .9107

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the probability distribution below. x
F(x)
10
)2
20
)3
30
)4
40
)1
The expected value of x equals
A) 24
B) 25
C) 30
D) 100
F(x)
10
)2
20
)3
30
)4
40
)1
The expected value of x equals
A) 24
B) 25
C) 30
D) 100

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
59
The probability distribution for the daily sales at Michael's Co.is given below.
The probability of having sales of at least $50,000 is
A) 0.5
B) 0.10
C) 0.30
D) 0.90
The probability of having sales of at least $50,000 is
A) 0.5
B) 0.10
C) 0.30
D) 0.90

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
60
Random variable x has the probability function: f(x) = x/6 for x =1,2 or 3.The expected value of x is
A) 0.333
B) 0.500
C) 2.000
D) 2.333
A) 0.333
B) 0.500
C) 2.000
D) 2.333

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
61
The probability distribution for the number of goals the Lions soccer team makes per game is given below.
What is the probability that in a given game the Lions will score less than 3 goals?
A) .85
B) .55
C) .45
D) .80
What is the probability that in a given game the Lions will score less than 3 goals?
A) .85
B) .55
C) .45
D) .80

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
62
A name closely associated with the binomial probability distribution is
A) Bernoulli.
B) de Moivre.
C) Pareto.
D) Poisson.
A) Bernoulli.
B) de Moivre.
C) Pareto.
D) Poisson.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
63
The probability distribution for the daily sales at Michael's Co.is given below.
The expected daily sales are
A) $50,000
B) $55,000
C) $56,000
D) $60,000
The expected daily sales are
A) $50,000
B) $55,000
C) $56,000
D) $60,000

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
64
To compute the probability that in a random sample of n elements, selected without replacement, we will obtain x successes, we would use the
A) binomial probability distribution.
B) Poisson probability distribution.
C) hypergeometric probability distribution.
D) exponential probability distribution.
A) binomial probability distribution.
B) Poisson probability distribution.
C) hypergeometric probability distribution.
D) exponential probability distribution.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
65
The _____ probability function is based in part on the counting rule for combinations.
A) binomial
B) Poisson
C) hypergeometric
D) exponential
A) binomial
B) Poisson
C) hypergeometric
D) exponential

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
66
A binomial probability distribution with p = .3 is
A) negatively skewed.
B) symmetric.
C) positively skewed.
D) multi-modal.
A) negatively skewed.
B) symmetric.
C) positively skewed.
D) multi-modal.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
67
If one wanted to find the probability of ten customer arrivals in an hour at a service station, one would generally use the
A) binomial probability distribution.
B) Poisson probability distribution.
C) hypergeometric probability distribution.
D) exponential probability distribution.
A) binomial probability distribution.
B) Poisson probability distribution.
C) hypergeometric probability distribution.
D) exponential probability distribution.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
68
In a binomial experiment the probability of success is 0.06.What is the probability of two successes in seven trials?
A) 0.0036
B) 0.06
C) 0.0554
D) 0.28
A) 0.0036
B) 0.06
C) 0.0554
D) 0.28

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
69
Assume that you have a binomial experiment with p= 0.4 and a sample size of 50.The variance of this distribution is?
A) 20
B) 12
C) 3.46
D) 2.83
A) 20
B) 12
C) 3.46
D) 2.83

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
70
The use of the relative frequency method to develop discrete probability distributions leads to what is called a
A) binomial discrete distribution.
B) empirical discrete distribution.
C) non-uniform discrete distribution.
D) uniform discrete distribution.
A) binomial discrete distribution.
B) empirical discrete distribution.
C) non-uniform discrete distribution.
D) uniform discrete distribution.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
71
Experiments with repeated independent trials will be described by the binomial distribution if
A) the trials are continuous.
B) each trial result influences the next.
C) the time between trials is constant.
D) each trial has exactly two outcomes whose probabilities do not change.
A) the trials are continuous.
B) each trial result influences the next.
C) the time between trials is constant.
D) each trial has exactly two outcomes whose probabilities do not change.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
72
The binomial probability distribution is most symmetric when
A) n is 30 or greater.
B) n equals p.
C) p approaches 1.
D) p equals 0.5.
A) n is 30 or greater.
B) n equals p.
C) p approaches 1.
D) p equals 0.5.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
73
A production process produces 2% defective parts.A sample of five parts from the production process is selected.What is the probability that the sample contains exactly two defective parts?
A) 0.0004
B) 0.0038
C) 0.10
D) 0.02
A) 0.0004
B) 0.0038
C) 0.10
D) 0.02

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
74
The number of electrical outages in a city varies from day to day.Assume that the number of electrical outages (x) in the city has the following probability distribution.
The mean and the standard deviation for the number of electrical outages (respectively) are
A) 2.6 and 5.77
B) 0.26 and 0.577
C) 3 and 0.01
D) 0 and 0.8
The mean and the standard deviation for the number of electrical outages (respectively) are
A) 2.6 and 5.77
B) 0.26 and 0.577
C) 3 and 0.01
D) 0 and 0.8

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
75
?In a Poisson probability problem, the rate of defects is one every two hours.To find the probability of three defects in four hours,
A)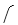 = 1, x = 4
= 1, x = 4
B) 11ef1cb7_756f_355c_98f1_c34873e26645_TB1213_11 = 2, x = 3
C) 11ef1cb7_756f_355c_98f1_c34873e26645_TB1213_11= 3, x = 4
D) 11ef1cb7_756f_355c_98f1_c34873e26645_TB1213_11 = 4, x = 3
A)
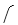 = 1, x = 4
= 1, x = 4B) 11ef1cb7_756f_355c_98f1_c34873e26645_TB1213_11 = 2, x = 3
C) 11ef1cb7_756f_355c_98f1_c34873e26645_TB1213_11= 3, x = 4
D) 11ef1cb7_756f_355c_98f1_c34873e26645_TB1213_11 = 4, x = 3

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
76
Experimental outcomes that are based on measurement scales such as time, weight, and distance can be described by _____ random variables.
A) discrete
B) continuous
C) uniform
D) intermittent
A) discrete
B) continuous
C) uniform
D) intermittent

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
77
In a binomial experiment consisting of five trials, the number of different values that x (the number of successes) can assume is
A) 2
B) 5
C) 6
D) 10
A) 2
B) 5
C) 6
D) 10

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
78
The weight of an object, measured to the nearest gram, is an example of
A) a continuous random variable.
B) a discrete random variable.
C) a nominal random variable.
D) a mixed type random variable.
A) a continuous random variable.
B) a discrete random variable.
C) a nominal random variable.
D) a mixed type random variable.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
79
Which of the following properties of a binomial experiment is called the stationarity assumption?
A) The experiment consists of n identical trials
B) Two outcomes are possible on each trial
C) The probability of success is the same for each trial
D) The trials are independent
A) The experiment consists of n identical trials
B) Two outcomes are possible on each trial
C) The probability of success is the same for each trial
D) The trials are independent

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
80
The probability distribution for the number of goals the Lions soccer team makes per game is given below. The expected number of goals per game is?
A) 2
B) 2.35
C) 2.5
D) 3
A) 2
B) 2.35
C) 2.5
D) 3

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck



