Deck 6: Point Estimation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/28
Play
Full screen (f)
Deck 6: Point Estimation
1
Which of the following statements are true if is a random sample from a distribution with mean ?
A) The sample mean
Is always an unbiased estimator of
)
B) The sample mean
Is an unbiased estimator of
If the distribution is continuous and symmetric.
C) Any trimmed mean is an unbiased estimator of
If the distribution is continuous and symmetric.
D) None of the above statements are true.
E) All of the above statements are true.
A) The sample mean
Is always an unbiased estimator of
)
B) The sample mean
Is an unbiased estimator of
If the distribution is continuous and symmetric.
C) Any trimmed mean is an unbiased estimator of
If the distribution is continuous and symmetric.
D) None of the above statements are true.
E) All of the above statements are true.
All of the above statements are true.
2
The sample median 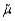 and any trimmed mean are unbiased estimators of the population mean
and any trimmed mean are unbiased estimators of the population mean  if the random sample from a population that is __________ and __________.
if the random sample from a population that is __________ and __________.
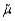 and any trimmed mean are unbiased estimators of the population mean
and any trimmed mean are unbiased estimators of the population mean  if the random sample from a population that is __________ and __________.
if the random sample from a population that is __________ and __________.continuous, symmetric
3
Given four observed values: 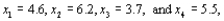 would result in a point estimate for
would result in a point estimate for 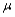 that is equal to __________.
that is equal to __________.
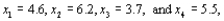 would result in a point estimate for
would result in a point estimate for 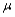 that is equal to __________.
that is equal to __________.5
4
Which of the following statements are true if is a random sample from a distribution with mean ?
A)
B)
C)
D)
E) All of the above statements are true provided that the sample size n > 30.
A)
B)
C)
D)
E) All of the above statements are true provided that the sample size n > 30.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
5
A point estimator 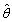 is said to be an __________ estimator of
is said to be an __________ estimator of 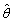 if
if 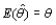 for every possible value of
for every possible value of 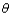 .
.
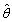 is said to be an __________ estimator of
is said to be an __________ estimator of 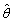 if
if 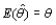 for every possible value of
for every possible value of 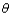 .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
6
In your text, two important methods were discussed for obtaining point estimates: the method of __________ and the method of __________.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
7
The standard error of an estimator 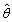 is the __________ of
is the __________ of 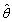 .
.
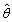 is the __________ of
is the __________ of 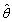 .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
8
Which of the following statements are not always true?
A) A point estimator
Is said to be an unbiased estimator of parameter
If
For every possible value of
)
B) If the estimator
Is not unbiased of parameter
, the difference
Is called the bias of
)
C) A point estimator
Is unbiased if its probability sampling distribution is always "centered" at the true value of the parameter
, where "centered" here means that the median of the distribution of
)
D) All of the above statements are true.
A) A point estimator
Is said to be an unbiased estimator of parameter
If
For every possible value of
)
B) If the estimator
Is not unbiased of parameter
, the difference
Is called the bias of
)
C) A point estimator
Is unbiased if its probability sampling distribution is always "centered" at the true value of the parameter
, where "centered" here means that the median of the distribution of
)
D) All of the above statements are true.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
9
The objective of __________ is to select a single number such as 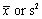 , based on sample data, that represents a sensible value (good guess) for the true value of the population parameter, such as
, based on sample data, that represents a sensible value (good guess) for the true value of the population parameter, such as  .
.
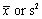 , based on sample data, that represents a sensible value (good guess) for the true value of the population parameter, such as
, based on sample data, that represents a sensible value (good guess) for the true value of the population parameter, such as  .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following statements are not always true?
A) It is necessary to know the true value of the parameter
To determine whether the estimator
Is unbiased.
B) When X is a binomial random variable with parameters n and p, the sample proportion
Is an unbiased estimator of p.
C) When choosing among several different estimators of parameter
, select one that is unbiased.
D) All of the above statements are not always true.
A) It is necessary to know the true value of the parameter
To determine whether the estimator
Is unbiased.
B) When X is a binomial random variable with parameters n and p, the sample proportion
Is an unbiased estimator of p.

C) When choosing among several different estimators of parameter
, select one that is unbiased.
D) All of the above statements are not always true.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
11
Which of the following statements are not true?
A) Maximum likelihood estimators are generally preferable to moment estimators because of certain efficiency properties.
B) Maximum likelihood estimators often require significantly more computation than do moment estimators.
C) The definition of unbiasedness in general indicates how unbiased estimators can be derived.
D) None of the above statements are true.
E) All of the above statements are true
A) Maximum likelihood estimators are generally preferable to moment estimators because of certain efficiency properties.
B) Maximum likelihood estimators often require significantly more computation than do moment estimators.
C) The definition of unbiasedness in general indicates how unbiased estimators can be derived.
D) None of the above statements are true.
E) All of the above statements are true

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following statements are not true?
A) Maximizing the likelihood function gives the parameter values for which the observed sample is most likely to have been generated---that is, the parameter values that "agree most likely" with the observed data.
B) Different principles of estimation may yield different estimators of the unknown parameters.
C) The maximum likelihood estimator of the population standard deviation
Is the sample standard deviation S.
D) None of the above statements are true.
A) Maximizing the likelihood function gives the parameter values for which the observed sample is most likely to have been generated---that is, the parameter values that "agree most likely" with the observed data.
B) Different principles of estimation may yield different estimators of the unknown parameters.
C) The maximum likelihood estimator of the population standard deviation
Is the sample standard deviation S.
D) None of the above statements are true.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
13
Which of the following statements are true?
A) A point estimate of a population parameter
Is a single number that can be regarded as a sensible value of
)
B) A point estimate of a population parameter
Is obtained by selecting a suitable statistic and computing its value from the given sample data. The selected statistic is called the point estimator of
)
C) The sample mean
Is a point estimator of the population mean
)
D) The sample variance
Is a point estimator of the population variance
)
E) All of the above statements are true.
A) A point estimate of a population parameter
Is a single number that can be regarded as a sensible value of
)
B) A point estimate of a population parameter
Is obtained by selecting a suitable statistic and computing its value from the given sample data. The selected statistic is called the point estimator of
)
C) The sample mean
Is a point estimator of the population mean
)
D) The sample variance
Is a point estimator of the population variance
)
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
14
Let  be a random sample from a probability mass function or probability density function f(x). For k = 1,2,3,……, the kth population moment is denoted by __________, while the kth sample moment is __________.
be a random sample from a probability mass function or probability density function f(x). For k = 1,2,3,……, the kth population moment is denoted by __________, while the kth sample moment is __________.
 be a random sample from a probability mass function or probability density function f(x). For k = 1,2,3,……, the kth population moment is denoted by __________, while the kth sample moment is __________.
be a random sample from a probability mass function or probability density function f(x). For k = 1,2,3,……, the kth population moment is denoted by __________, while the kth sample moment is __________.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
15
Let  be a random sample of size n from an exponential distribution with parameter
be a random sample of size n from an exponential distribution with parameter 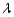 . The moment estimator of
. The moment estimator of 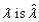 = __________.
= __________.
 be a random sample of size n from an exponential distribution with parameter
be a random sample of size n from an exponential distribution with parameter 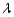 . The moment estimator of
. The moment estimator of 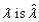 = __________.
= __________.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following statements are correct?
A) The first population moment is
, while the first sample moment is
)
B) The moment estimators
Are obtained by equating the first m sample moments to the corresponding first m population moments, and solving for the unknown parameters
)
C) The method of maximum likelihood was first introduced by R.A. Fisher, a geneticist and statistician, in the 1920's.
D) All of the above statements are true.
E) Only (A) and (B) are true.
A) The first population moment is
, while the first sample moment is
)
B) The moment estimators
Are obtained by equating the first m sample moments to the corresponding first m population moments, and solving for the unknown parameters
)
C) The method of maximum likelihood was first introduced by R.A. Fisher, a geneticist and statistician, in the 1920's.
D) All of the above statements are true.
E) Only (A) and (B) are true.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
17
Among all estimators of parameter 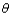 that are unbiased, choose the one that has minimum variance. The resulting
that are unbiased, choose the one that has minimum variance. The resulting  is called the __________ of
is called the __________ of  .
.
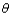 that are unbiased, choose the one that has minimum variance. The resulting
that are unbiased, choose the one that has minimum variance. The resulting  is called the __________ of
is called the __________ of  .
.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following statements are not true?
A) The symbol
Is customarily used to denote the estimator of parameter
And the point estimate resulting from a given sample.
B) The equality
Is read as "the point estimator of
C) The difference between
And the parameter
Is referred to as error of estimation.
D) None of the above statements is true.
A) The symbol
Is customarily used to denote the estimator of parameter
And the point estimate resulting from a given sample.
B) The equality
Is read as "the point estimator of
C) The difference between
And the parameter
Is referred to as error of estimation.
D) None of the above statements is true.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
19
Let 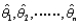 be the maximum likelihood estimates (mle's) of the parameters
be the maximum likelihood estimates (mle's) of the parameters 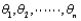 . Then the mle of any function h(
. Then the mle of any function h( 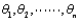 ) of these parameters is the function
) of these parameters is the function 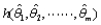 of the mle's. This result is known as the __________ principle.
of the mle's. This result is known as the __________ principle.
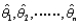 be the maximum likelihood estimates (mle's) of the parameters
be the maximum likelihood estimates (mle's) of the parameters 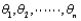 . Then the mle of any function h(
. Then the mle of any function h( 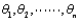 ) of these parameters is the function
) of these parameters is the function 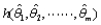 of the mle's. This result is known as the __________ principle.
of the mle's. This result is known as the __________ principle.
Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
20
An estimator that has the properties of __________ and __________ will often be regarded as an accurate estimator.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
21
A random sample of
a. Derive the maximum likelihood estimator of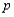
. If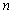
= 25 and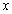
=5, what is the estimate?
b. Is the estimator of part (a) unbiased?
c. If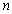
= 25 and
=5, what is the mle of the probability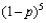
that none of the next five helmets examined is flawed?
a. Derive the maximum likelihood estimator of
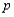
. If
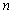
= 25 and
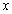
=5, what is the estimate?
b. Is the estimator of part (a) unbiased?
c. If
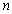
= 25 and

=5, what is the mle of the probability
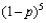
that none of the next five helmets examined is flawed?

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
22
Let 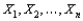 represent a random sample from a Rayleigh distribution with pdf
represent a random sample from a Rayleigh distribution with pdf 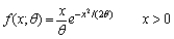
a. It can be shown that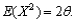
Use this fact to construct an unbiased estimator of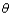
based on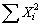
(and use rules of expected value to show that it is unbiased).
b. Estimate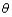
from the following
observations on vibratory stress of a turbine blade under specified conditions:
17.08 10.43 4.79 6.86 13.88
14.43 20.07 9.60 6.71 11.15
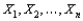 represent a random sample from a Rayleigh distribution with pdf
represent a random sample from a Rayleigh distribution with pdf 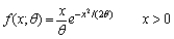
a. It can be shown that
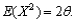
Use this fact to construct an unbiased estimator of
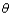
based on
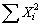
(and use rules of expected value to show that it is unbiased).
b. Estimate
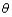
from the following

observations on vibratory stress of a turbine blade under specified conditions:
17.08 10.43 4.79 6.86 13.88
14.43 20.07 9.60 6.71 11.15

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
23
Consider a random sample 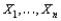 from the pdf
from the pdf 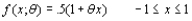 where
where 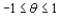 (this distribution arises in particle physics). Show that
(this distribution arises in particle physics). Show that 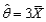 is an unbiased estimator of
is an unbiased estimator of 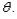 [
[  Hint: First determine
Hint: First determine 
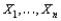 from the pdf
from the pdf 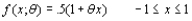 where
where 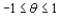 (this distribution arises in particle physics). Show that
(this distribution arises in particle physics). Show that 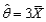 is an unbiased estimator of
is an unbiased estimator of 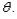 [
[  Hint: First determine
Hint: First determine 

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
24
Let  denote the proportion of allotted time that a randomly selected student spends working on a certain aptitude test. Suppose the pdf of
denote the proportion of allotted time that a randomly selected student spends working on a certain aptitude test. Suppose the pdf of 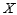 is
is 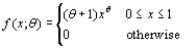 where
where 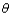 > -1. A random sample of ten students yields data
> -1. A random sample of ten students yields data 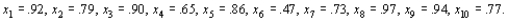
a. Use the method of moments to obtain an estimator of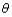
and then compute the estimate for this data.
b. Obtain the maximum likelihood estimator of
and then compute the estimate for the given data.
 denote the proportion of allotted time that a randomly selected student spends working on a certain aptitude test. Suppose the pdf of
denote the proportion of allotted time that a randomly selected student spends working on a certain aptitude test. Suppose the pdf of 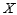 is
is 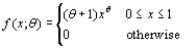 where
where 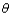 > -1. A random sample of ten students yields data
> -1. A random sample of ten students yields data 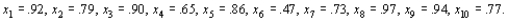
a. Use the method of moments to obtain an estimator of
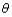
and then compute the estimate for this data.
b. Obtain the maximum likelihood estimator of

and then compute the estimate for the given data.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
25
The accompanying data describe flexural strength (Mpa) for concrete beams of a certain type was introduced in Example 1.2.
A) Calculate a point estimate of the mean value of strength for the conceptual population of all beams manufactured in this fashion, and state which estimator you used. Hint:
B) Calculate a point estimate of the strength value that separates the weakest 50% of all such beams from the strongest 50%, and state which estimator you used.
C) Calculate and interpret a point estimate of the population standard deviation
Which estimator did you use? Hint:
D) Calculate a point estimate of the proportion of all such beams whose flexural strength exceeds 11 Mpa. Hint: Think of an observation as a "success" if it exceeds 11.
E) Calculate a point estimate of the population coefficient of variation
And state which estimator you used.
A) Calculate a point estimate of the mean value of strength for the conceptual population of all beams manufactured in this fashion, and state which estimator you used. Hint:
B) Calculate a point estimate of the strength value that separates the weakest 50% of all such beams from the strongest 50%, and state which estimator you used.
C) Calculate and interpret a point estimate of the population standard deviation
Which estimator did you use? Hint:
D) Calculate a point estimate of the proportion of all such beams whose flexural strength exceeds 11 Mpa. Hint: Think of an observation as a "success" if it exceeds 11.
E) Calculate a point estimate of the population coefficient of variation
And state which estimator you used.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
26
Consider a random sample 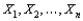 from the shifted exponential pdf
from the shifted exponential pdf 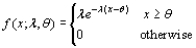
a. Obtain the maximum likelihood estimators of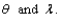
b. A random sample of size
results in the values 3.12, .65, 2.56, 2.21, 5.45, 3.43, 10.40, 8.94, 17.83, and 1.31, calculate the estimates of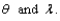
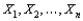 from the shifted exponential pdf
from the shifted exponential pdf 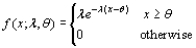
a. Obtain the maximum likelihood estimators of
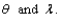
b. A random sample of size

results in the values 3.12, .65, 2.56, 2.21, 5.45, 3.43, 10.40, 8.94, 17.83, and 1.31, calculate the estimates of
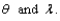

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
27
Which of the following statements are true?
A) Maximizing the likelihood estimation is the most widely used estimation technique among statisticians.
B) Under very general conditions on the joint distribution of the sample, when the sample size n is large, the maximum likelihood estimator of any parameter
Is approximately unbiased; that is,
)
C) Under very general conditions on the joint distribution of the sample, when the sample size n is large, the maximum likelihood estimator of any parameter
Has variance, is nearly as small as small as can be achieved by any estimator.
D) In recent years, statisticians have proposed an estimator, called an M-estimator, which is based on a generalization of maximum likelihood estimation.
E) All of the above are true statements.
A) Maximizing the likelihood estimation is the most widely used estimation technique among statisticians.
B) Under very general conditions on the joint distribution of the sample, when the sample size n is large, the maximum likelihood estimator of any parameter
Is approximately unbiased; that is,
)
C) Under very general conditions on the joint distribution of the sample, when the sample size n is large, the maximum likelihood estimator of any parameter
Has variance, is nearly as small as small as can be achieved by any estimator.
D) In recent years, statisticians have proposed an estimator, called an M-estimator, which is based on a generalization of maximum likelihood estimation.
E) All of the above are true statements.

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck
28
The shear strength of each of ten test spot welds is determined, yielding the following data (psi): 
a. Assuming that shear strength is normally distributed, estimate the true average shear strength and standard deviation of shear strength using the method of maximum likelihood.
b. Again assuming a normal distribution, estimate the strength value below which 95% of all welds will have their strengths. (Hint: What is the 95 percentile in terms of
? Now use the invariance principle.)

a. Assuming that shear strength is normally distributed, estimate the true average shear strength and standard deviation of shear strength using the method of maximum likelihood.
b. Again assuming a normal distribution, estimate the strength value below which 95% of all welds will have their strengths. (Hint: What is the 95 percentile in terms of

? Now use the invariance principle.)

Unlock Deck
Unlock for access to all 28 flashcards in this deck.
Unlock Deck
k this deck



