Deck 15: Distribution-Free Procedures
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/66
Play
Full screen (f)
Deck 15: Distribution-Free Procedures
1
For large samples when the underlying population is normal, the Wilcoxon signed-rank interval will tend to be slightly __________ than the t interval.
longer
2
Let 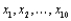 be a random sample from a continuous and symmetric probability distribution with mean (and median)
be a random sample from a continuous and symmetric probability distribution with mean (and median) 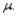 In testing
In testing 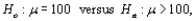 using the Wilcoxon signed-rank test, the rejection region for level .01 test is
using the Wilcoxon signed-rank test, the rejection region for level .01 test is 
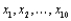 be a random sample from a continuous and symmetric probability distribution with mean (and median)
be a random sample from a continuous and symmetric probability distribution with mean (and median) 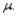 In testing
In testing 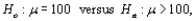 using the Wilcoxon signed-rank test, the rejection region for level .01 test is
using the Wilcoxon signed-rank test, the rejection region for level .01 test is 
5
3
Because the t and F procedures require the distributional assumption of normality, they are not __________ procedures.
distribution free
4
Suppose that a random sample of size 30 from a normal population is used to test 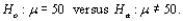 The t test at level .10 specifies that
The t test at level .10 specifies that 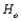 should be rejected if the test statistic value t is either
should be rejected if the test statistic value t is either 
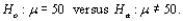 The t test at level .10 specifies that
The t test at level .10 specifies that 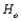 should be rejected if the test statistic value t is either
should be rejected if the test statistic value t is either 

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
5
The Wilcoxon rank-sum test statistic W is the sum of the ranks in the combined X and Y sample observations associated with __________ observations.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
6
Because the t and F procedures are based on a particular parametric family of distributions (normal), they are not __________ procedures.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
7
For n = 8 observations, there are __________ possible signed-rank sequences, and to list these sequences would be very tedious.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
8
For values of m (number of observed x values) and n (number of observed y values) that exceed __________, a normal approximation for the distribution of the Wilcoxon rank-sum statistic W can be used.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
9
A 95% distribution-free confidence interval for a parameter 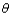 can be obtained from a level __________ test for
can be obtained from a level __________ test for 
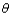 can be obtained from a level __________ test for
can be obtained from a level __________ test for 

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
10
The asymptotic relative efficiency (ARE) of one test with respect to another is essentially the limiting ratio of the __________ necessary to obtain identical error probabilities for the two tests.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose  Then, the computed value of the Wilcoxon rank-sum test statistic W is w = __________.
Then, the computed value of the Wilcoxon rank-sum test statistic W is w = __________.
 Then, the computed value of the Wilcoxon rank-sum test statistic W is w = __________.
Then, the computed value of the Wilcoxon rank-sum test statistic W is w = __________.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
12
For any distribution, the asymptotic relative efficiency (ARE) will be at least __________, and for many distributions will be much greater than 1.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
13
The Wilcoxon rank-sum test is applied to three values of x and four values of y. Then, the smallest possible value of the test statistic W is w = __________ and the largest possible value is w = __________.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
14
For large samples when the underlying population is quite nonnormal (symmetric but with heavy tails), the Wilcoxon signed-rank interval will tend to be much __________ than the t interval.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
15
When the underlying distribution is normal, the asymptotic relative efficiency (ARE) of the Wilcoxon signed-rank test with respect to the t test is approximately __________.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
16
The table of critical values for the Wilcoxon signed-rank test, as shown in your text, provides critical values for level 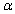 tests only when n is less than or equal to __________.
tests only when n is less than or equal to __________.
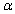 tests only when n is less than or equal to __________.
tests only when n is less than or equal to __________.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
17
When the underlying distribution being sampled is normal, the t test or the Wilcoxon signed-rank test can be used to test a hypothesis about the population mean 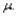 However, the __________ is the best test in such a situation because among all level
However, the __________ is the best test in such a situation because among all level 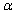 tests it is the one having minimum
tests it is the one having minimum 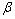 (i.e., minimum probability of Type II error)
(i.e., minimum probability of Type II error)
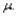 However, the __________ is the best test in such a situation because among all level
However, the __________ is the best test in such a situation because among all level 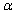 tests it is the one having minimum
tests it is the one having minimum 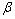 (i.e., minimum probability of Type II error)
(i.e., minimum probability of Type II error)
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
18
An alternative name for the Wilcoxon rank-sum test is the __________ test.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
19
The observed value of the Wilcoxon Signed-Rank Test statistic 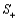 is the sum of the ranks associated with the __________ observations.
is the sum of the ranks associated with the __________ observations.
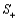 is the sum of the ranks associated with the __________ observations.
is the sum of the ranks associated with the __________ observations.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
20
Let 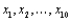 be a random sample from a continuous and symmetric probability distribution with mean (and median)
be a random sample from a continuous and symmetric probability distribution with mean (and median) 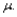 In testing
In testing 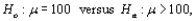 using the Wilcoxon signed-rank test, the rejection region for level .01 test is
using the Wilcoxon signed-rank test, the rejection region for level .01 test is 
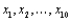 be a random sample from a continuous and symmetric probability distribution with mean (and median)
be a random sample from a continuous and symmetric probability distribution with mean (and median) 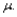 In testing
In testing 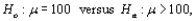 using the Wilcoxon signed-rank test, the rejection region for level .01 test is
using the Wilcoxon signed-rank test, the rejection region for level .01 test is 

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following statements are not true?
A) Any normal distribution is symmetric, so symmetry is actually a weaker assumption than normality.
B) Any symmetric distribution is normal, so normality is actually a weaker assumption than symmetry.
C) When testing
Versus
(
Is the median) using the Wilcoxon signed-rank test,
Is rejected when the test statistic value
Is too large because a large value of
Indicates that most of the observations with large absolute magnitude are positive, which in turn indicates a median greater than 0.
D) When the data consists of pairs
And the differences
(i =1, . . . . . . ,n )
Are normally distributed, a paired t test is used to test hypotheses about the expected difference
E) All of the above statements are true.
A) Any normal distribution is symmetric, so symmetry is actually a weaker assumption than normality.
B) Any symmetric distribution is normal, so normality is actually a weaker assumption than symmetry.
C) When testing
Versus
(
Is the median) using the Wilcoxon signed-rank test,
Is rejected when the test statistic value
Is too large because a large value of
Indicates that most of the observations with large absolute magnitude are positive, which in turn indicates a median greater than 0.
D) When the data consists of pairs
And the differences
(i =1, . . . . . . ,n )
Are normally distributed, a paired t test is used to test hypotheses about the expected difference
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
22
Which of the following statements are not true?
A) When the underlying distribution being sampled has "heavy tails"; that is, when observed values lying far from population mean
Are relatively more likely than they are when the distribution is normal, the t test can perform poorly.
B) If the asymptotic relative efficiency (ARE) of one test with respect to a second equals .50, then when sample sizes are large, twice as large a sample size will be required of the first test to perform as well as the second test.
C) When the underlying distribution is normal, the asymptotic relative efficiency of the Wilcoxon signed-rank test with respect to the t test is approximately .95.
D) For any distribution, the asymptotic relative efficiency will be at least .86, and for many distributions it will be much greater than 2.
E) All of the above statements are true.
A) When the underlying distribution being sampled has "heavy tails"; that is, when observed values lying far from population mean
Are relatively more likely than they are when the distribution is normal, the t test can perform poorly.
B) If the asymptotic relative efficiency (ARE) of one test with respect to a second equals .50, then when sample sizes are large, twice as large a sample size will be required of the first test to perform as well as the second test.
C) When the underlying distribution is normal, the asymptotic relative efficiency of the Wilcoxon signed-rank test with respect to the t test is approximately .95.
D) For any distribution, the asymptotic relative efficiency will be at least .86, and for many distributions it will be much greater than 2.
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following statements are true?
A) The Wilcoxon rank-sum test procedure is not distribution-free because it will not have the desired level of significance for a very large class of underlying distributions.
B) If there are three observed values of x and five observed values of y, then the smallest possible value of the Wilcoxon rank-sum test statistic W is w = 6 and the largest possible value is w = 21.
C) When the distributions being sampled are both normal with
And therefore have the same shapes and spreads, only the pooled t test can be used in testing
Whereas the Wilcoxon rank-sum test should not be used because it is distribution-free.
D) When normality and equal variances both hold, the Wilcoxon rank-sum test is approximately 75% as efficient as the pooled t test in large samples.
E) All of the above statements are true.
A) The Wilcoxon rank-sum test procedure is not distribution-free because it will not have the desired level of significance for a very large class of underlying distributions.
B) If there are three observed values of x and five observed values of y, then the smallest possible value of the Wilcoxon rank-sum test statistic W is w = 6 and the largest possible value is w = 21.
C) When the distributions being sampled are both normal with
And therefore have the same shapes and spreads, only the pooled t test can be used in testing
Whereas the Wilcoxon rank-sum test should not be used because it is distribution-free.
D) When normality and equal variances both hold, the Wilcoxon rank-sum test is approximately 75% as efficient as the pooled t test in large samples.
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
24
Let N be the total number of observations in a data set, and suppose we rank all N observations from 1 (the smallest 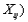 to N (the largest
to N (the largest 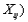 . When
. When 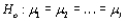 is true, and
is true, and  denotes the rank of
denotes the rank of  among the N observations, then
among the N observations, then 
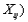 to N (the largest
to N (the largest 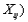 . When
. When 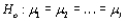 is true, and
is true, and  denotes the rank of
denotes the rank of  among the N observations, then
among the N observations, then 

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
25
When 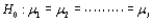 is true, and either the number of population or treatment means I = 3 and the sample size
is true, and either the number of population or treatment means I = 3 and the sample size 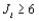 (i = 1,2,3), or I > 3 and
(i = 1,2,3), or I > 3 and 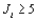 (i = 1,
(i = 1,  ,I), then the Kruskal-Wallis test statistic K has approximately a __________ distribution with __________ degrees of freedom.
,I), then the Kruskal-Wallis test statistic K has approximately a __________ distribution with __________ degrees of freedom.
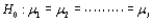 is true, and either the number of population or treatment means I = 3 and the sample size
is true, and either the number of population or treatment means I = 3 and the sample size 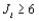 (i = 1,2,3), or I > 3 and
(i = 1,2,3), or I > 3 and 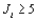 (i = 1,
(i = 1,  ,I), then the Kruskal-Wallis test statistic K has approximately a __________ distribution with __________ degrees of freedom.
,I), then the Kruskal-Wallis test statistic K has approximately a __________ distribution with __________ degrees of freedom.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
26
Which of the following tests would be an example of a distribution-free procedure?
A) The t test for population mean
B) The paired t test for the expected difference
C) The F test for two or more population means
D) The Wilcoxon rank-sum test
E) Only A and B are correct tests
A) The t test for population mean
B) The paired t test for the expected difference
C) The F test for two or more population means
D) The Wilcoxon rank-sum test
E) Only A and B are correct tests

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
27
When 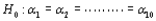 is tested using the Friedman's test statistic
is tested using the Friedman's test statistic 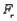 with significance level .025 (where
with significance level .025 (where 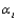 is the i th treatment effect), then
is the i th treatment effect), then 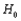 is rejected if
is rejected if 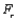 is greater than or equal to __________.
is greater than or equal to __________.
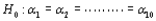 is tested using the Friedman's test statistic
is tested using the Friedman's test statistic 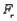 with significance level .025 (where
with significance level .025 (where 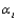 is the i th treatment effect), then
is the i th treatment effect), then 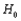 is rejected if
is rejected if 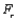 is greater than or equal to __________.
is greater than or equal to __________.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
28
Which of the following statements are not true?
A) When at least one of the sample sizes in a two-sample problem is small, the t test requires the assumption of normality (at least approximately).
B) The Wilcoxon rank-sum test statistic W is the sum of the ranks in the combined (X, Y) sample associated with X observations.
C) Because the Wilcoxon rank-sum test statistic W has a continuous probability distribution, there will always be a critical value corresponding exactly to one of the usual levels of significance.
D) All of the above statements are true.
E) None of the above statements are true.
A) When at least one of the sample sizes in a two-sample problem is small, the t test requires the assumption of normality (at least approximately).
B) The Wilcoxon rank-sum test statistic W is the sum of the ranks in the combined (X, Y) sample associated with X observations.
C) Because the Wilcoxon rank-sum test statistic W has a continuous probability distribution, there will always be a critical value corresponding exactly to one of the usual levels of significance.
D) All of the above statements are true.
E) None of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
29
When ranking data in a Wilcoxon signed-rank test, the data value that receives a rank of 1 is the
A) largest value regardless of its size
B) smallest value regardless of its size
C) middle value regardless of its size
D) 25th percentile value
E) 75th percentile value
A) largest value regardless of its size
B) smallest value regardless of its size
C) middle value regardless of its size
D) 25th percentile value
E) 75th percentile value

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
30
Friedman's test for a randomized block experiment rejects 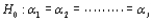 (where
(where 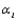 is the i th treatment effect) when the computed value of the test statistic
is the i th treatment effect) when the computed value of the test statistic 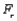 is too __________.
is too __________.
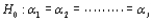 (where
(where 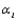 is the i th treatment effect) when the computed value of the test statistic
is the i th treatment effect) when the computed value of the test statistic 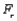 is too __________.
is too __________.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
31
The Wilcoxon signed-rank interval uses pairwise averages from a single sample, whereas the Wilcoxon rank-sum interval uses pairwise differences from __________ samples.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
32
When 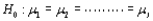 is tested using the Kruskal-Wallis test statistic K with approximate significance level
is tested using the Kruskal-Wallis test statistic K with approximate significance level 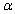 , then
, then 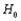 is rejected if K is greater than or equal to __________.
is rejected if K is greater than or equal to __________.
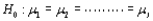 is tested using the Kruskal-Wallis test statistic K with approximate significance level
is tested using the Kruskal-Wallis test statistic K with approximate significance level 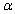 , then
, then 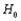 is rejected if K is greater than or equal to __________.
is rejected if K is greater than or equal to __________.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
33
Which of the following statements are true?
A) In large-sample problems, the Wilcoxon signed-rank test is never very much less efficient than the t test and may be much more efficient if the underlying distribution is far from normal.
B) The Wilcoxon signed-rank test statistic for large-sample is
Where n is the sample size and
Is the sum of the ranks associated with the positive observations.
C) When the sample size n > 20, the Wilcoxon signed-rank test statistic
Has approximately a normal distribution with mean and variance given by
, respectively
D) All of the above statements are true.
E) None of the above statements are true.
A) In large-sample problems, the Wilcoxon signed-rank test is never very much less efficient than the t test and may be much more efficient if the underlying distribution is far from normal.
B) The Wilcoxon signed-rank test statistic for large-sample is
Where n is the sample size and
Is the sum of the ranks associated with the positive observations.
C) When the sample size n > 20, the Wilcoxon signed-rank test statistic
Has approximately a normal distribution with mean and variance given by
, respectively
D) All of the above statements are true.
E) None of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
34
Which of the following statements are not true?
A) When m and n (number of observed x values and y values, respectively, in the combined sample) exceed 8, the Wilcoxon rank-sum test statistic W has approximately a t distribution with m + n - 1 degrees of freedom
B) The table of critical values for the Wilcoxon rank-sum test, which is available in your text, gives information only for
Where m and n are the number of observed x and y values, respectively, in the combined sample.
C) If m and n are the number of observed x and y values, respectively, in the combined sample, then to use the table of critical values for the Wilcoxon rank-sum test, which is available in your text, the X and Y samples should be labeled so that
D) As with the Wilcoxon signed-rank test, the common practice in dealing with ties when using the Mann-Whitney test is to assign each of the tied observations in a particular set of ties the average of the ranks they would require if they differed very slightly from one another.
E) All of the above statements are true.
A) When m and n (number of observed x values and y values, respectively, in the combined sample) exceed 8, the Wilcoxon rank-sum test statistic W has approximately a t distribution with m + n - 1 degrees of freedom
B) The table of critical values for the Wilcoxon rank-sum test, which is available in your text, gives information only for
Where m and n are the number of observed x and y values, respectively, in the combined sample.
C) If m and n are the number of observed x and y values, respectively, in the combined sample, then to use the table of critical values for the Wilcoxon rank-sum test, which is available in your text, the X and Y samples should be labeled so that
D) As with the Wilcoxon signed-rank test, the common practice in dealing with ties when using the Mann-Whitney test is to assign each of the tied observations in a particular set of ties the average of the ranks they would require if they differed very slightly from one another.
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
35
A random sample of size 24 is drawn from a continuous and symmetric probability distribution with mean In testing it can be shown that the Wilcoxon signed-rank test statistic has approximately a normal distribution with mean and standard deviation given, respectively, by
A) 150 and 35
B) 25 and 300
C) 150 and 300
D) 35 and 25
E) 25 and 35
A) 150 and 35
B) 25 and 300
C) 150 and 300
D) 35 and 25
E) 25 and 35

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following tests would be an example of a nonparametric procedure?
A) Wilcoxon signed-rank test
B) The t test for population mean
C) The F test for population means
D) All of the above tests are correct.
E) Only B and C are correct tests.
A) Wilcoxon signed-rank test
B) The t test for population mean
C) The F test for population means
D) All of the above tests are correct.
E) Only B and C are correct tests.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
37
A random sample of size 15 is drawn from a continuous and symmetric probability distribution with mean In testing using the Wilcoxon signed-rank test with approximate level of significance of .05, the rejection region for the test is
A)
B)
C) either
Or
D)
E)
A)
B)
C) either
Or
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
38
For moderate values of the number of blocks J, the Friedman's test statistic 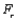 has approximately a __________ distribution with __________ degrees of freedom, where I is the number of treatments.
has approximately a __________ distribution with __________ degrees of freedom, where I is the number of treatments.
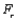 has approximately a __________ distribution with __________ degrees of freedom, where I is the number of treatments.
has approximately a __________ distribution with __________ degrees of freedom, where I is the number of treatments.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following statements are not true?
A) The t and F procedures are not "distribution-free" procedures because they require the distributed assumption of normality.
B) The t and F procedures are not "nonparametric" procedures because they are based on the normal parametric family of distribution.
C) Distribution-free and nonparametric procedures are valid for very few different types of underlying distributions.
D) Generally speaking, the distribution-free procedures perform almost as well as their t and F counterparts on the "home ground" of the normal distribution, and will often yield a considerable improvement under nonnormal conditions.
E) All of the above statements are true.
A) The t and F procedures are not "distribution-free" procedures because they require the distributed assumption of normality.
B) The t and F procedures are not "nonparametric" procedures because they are based on the normal parametric family of distribution.
C) Distribution-free and nonparametric procedures are valid for very few different types of underlying distributions.
D) Generally speaking, the distribution-free procedures perform almost as well as their t and F counterparts on the "home ground" of the normal distribution, and will often yield a considerable improvement under nonnormal conditions.
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following statements are true?
A) When the data consists of pairs
And the differences
(i = 1, . . . . . . ,n )
Are not assumed to be normally distributed, hypotheses tests about the expected differences
Can be tested by using the Wilcoxon signed-rank test on the
Provided that the distribution of the differences is continuous and symmetric.
B) When the sample size n is larger than 20, it can be shown that the Wilcoxon signed-rank test statistic
Has approximately a normal distribution when the null hypothesis is true.
C) When the underlying distribution being sampled is normal, either the t test or the Wilcoxon signed-rank test can be used to test a hypothesis about the population mean
D) A number of different efficiency measures have been proposed by statisticians; one that many statisticians regard as credible is called asymptotic relative efficiency (ARE).
E) All of the above statements are true.
A) When the data consists of pairs
And the differences
(i = 1, . . . . . . ,n )
Are not assumed to be normally distributed, hypotheses tests about the expected differences
Can be tested by using the Wilcoxon signed-rank test on the
Provided that the distribution of the differences is continuous and symmetric.
B) When the sample size n is larger than 20, it can be shown that the Wilcoxon signed-rank test statistic
Has approximately a normal distribution when the null hypothesis is true.
C) When the underlying distribution being sampled is normal, either the t test or the Wilcoxon signed-rank test can be used to test a hypothesis about the population mean
D) A number of different efficiency measures have been proposed by statisticians; one that many statisticians regard as credible is called asymptotic relative efficiency (ARE).
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
41
The nonparametric counterpart of the parametric single-factor ANOVA F-test is the
A) Wilcoxon signed-rank test.
B) Wilcoxon rank-sum test.
C) Kruskal-Wallis test.
D) Friedman's test.
E) None of the above tests are correct.
A) Wilcoxon signed-rank test.
B) Wilcoxon rank-sum test.
C) Kruskal-Wallis test.
D) Friedman's test.
E) None of the above tests are correct.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
42
Which of the following statements are not true?
A) A general method for obtaining confidence intervals takes advantage of a relationship between test procedures and confidence intervals; a
% confidence interval for a parameter
Can be obtained from a level
Test for
B) To test
Using the Wilcoxon signed-rank test, where
Is the mean of a continuous symmetric distribution, the absolute values
Are ordered from largest to smallest, with the largest receiving rank 1 and the smallest receiving rank n. Each rank is then given the sign of its associated
And the test statistic is the sum of the positively signed ranks.
C) For fixed
Wilcoxon signed-rank interval will consist of all
For which
Is not rejected at level
Where
Is the mean of a continuous symmetric distribution.
D) All of the above statements are true.
E) None of the above statements are true.
A) A general method for obtaining confidence intervals takes advantage of a relationship between test procedures and confidence intervals; a
% confidence interval for a parameter
Can be obtained from a level
Test for
B) To test
Using the Wilcoxon signed-rank test, where
Is the mean of a continuous symmetric distribution, the absolute values
Are ordered from largest to smallest, with the largest receiving rank 1 and the smallest receiving rank n. Each rank is then given the sign of its associated
And the test statistic is the sum of the positively signed ranks.
C) For fixed
Wilcoxon signed-rank interval will consist of all
For which
Is not rejected at level
Where
Is the mean of a continuous symmetric distribution.
D) All of the above statements are true.
E) None of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
43
Which of the following statements are not true?
A) The efficiency of the Wilcoxon signed-rank interval relative to the t interval is roughly the same as that for the Wilcoxon test relative to the t test.
B) For large samples when the underlying population is normal, the Wilcoxon signed-rank interval will tend to be slightly longer than the t interval.
C) For large samples when the underlying population is quite nonnormal (symmetric but with heavy tails), then the Wilcoxon signed-rank interval will tend to be much shorter than the t interval.
D) All of the above statements are true.
E) None of the above statements are true.
A) The efficiency of the Wilcoxon signed-rank interval relative to the t interval is roughly the same as that for the Wilcoxon test relative to the t test.
B) For large samples when the underlying population is normal, the Wilcoxon signed-rank interval will tend to be slightly longer than the t interval.
C) For large samples when the underlying population is quite nonnormal (symmetric but with heavy tails), then the Wilcoxon signed-rank interval will tend to be much shorter than the t interval.
D) All of the above statements are true.
E) None of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
44
The accompanying 25 observations on fracture toughness of base plate of 18% nickel maraging steel were obtained. Suppose a company will agree to purchase this steel for a particular application only if it can be strongly demonstrated from experimental evidence that "true" average toughness exceeds 80. Assuming that the fracture toughness distribution is symmetric, state and test the appropriate hypotheses level .05 and compute a P-value. 


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
45
The Friedman's test is always
A) two-tailed test
B) one-tailed test
C) used with one sample
D) used when the populations are normally distributed.
E) Used with matched-pairs samples
A) two-tailed test
B) one-tailed test
C) used with one sample
D) used when the populations are normally distributed.
E) Used with matched-pairs samples

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following distributions approximate the Kruskal-Wallis test statistic K when is true, and the number of populations or treatments I=3 and the sample sizes
A) Standard normal distribution
B) T distribution with I-1 degrees of freedom
C) F distribution with I-1 and
Degrees of freedom.
D) Chi-squared distribution with I-1 degrees of freedom.
E) Either B or C.
A) Standard normal distribution
B) T distribution with I-1 degrees of freedom
C) F distribution with I-1 and
Degrees of freedom.
D) Chi-squared distribution with I-1 degrees of freedom.
E) Either B or C.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
47
A random sample of 15 automobile mechanics certified to work on a certain type of car was selected, and the time (in minutes) necessary for each one to diagnose a particular problem was determined, resulting in the following data: 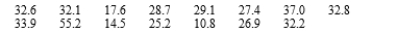 Use the Wilcoxon test at significance level .10 to decide whether the data suggests that "true" average diagnostic time is less than 32 minutes.
Use the Wilcoxon test at significance level .10 to decide whether the data suggests that "true" average diagnostic time is less than 32 minutes.
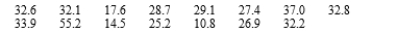 Use the Wilcoxon test at significance level .10 to decide whether the data suggests that "true" average diagnostic time is less than 32 minutes.
Use the Wilcoxon test at significance level .10 to decide whether the data suggests that "true" average diagnostic time is less than 32 minutes.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
48
A sample of size 8 is selected at random from a continuous symmetric distribution. A 95% Wilcoxon signed-rank interval (actually 94.5%) has the form
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
49
The Kruskal-Wallis test is always
A) two-tailed test.
B) one-tailed test.
C) used with one sample.
D) Used when the populations are normally distributed.
E) Used with match-pairs samples
A) two-tailed test.
B) one-tailed test.
C) used with one sample.
D) Used when the populations are normally distributed.
E) Used with match-pairs samples

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
50
Two independent random samples of sizes 5 and 7 are selected from two continuous distributions with means and that the two distributions have the same shape and spread. In testing using the Wilcoxon rank-sum test with approximate significance level of .05, the rejection region for the test is
A) either
B) either
C) either
D) either
E) either
A) either
B) either
C) either
D) either
E) either

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
51
The following observations are amounts of hydrocarbon emissions resulting from road wear of bias-belted tires under a 522-kg load inflated at 228 kPa and driven at 64 km/hr for 6 hours: 048, .120, .065, and .075. What confidence levels are achievable for this sample size using the signed-rank interval? Select an appropriate confidence level and compute the interval.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
52
Which of the following statements are true?
A) The Wilcoxon rank-sum test for testing
Is carried out by first combining the
Into one sample of size m + n and ranking them from smallest (rank 1) to largest (rank m + n). The test statistic W is then the sum of the ranks of the
B) The Wilcoxon rank-sum interval is very similar to the Wilcoxon signed=rank interval; the later uses pairwise averages from a single sample, whereas the former uses pairwise differences from two samples
C) The Wilcoxon rank-sum interval is quite efficient with respect to the t interval.
D) For large samples, the Wilcoxon rank-sum interval will tend to be only a bit longer than the t interval when the underlying populations are normal, and may be considerably shorter than the t interval if the underlying populations have heavier tails than do normal populations.
E) All of the above statements are true.
A) The Wilcoxon rank-sum test for testing
Is carried out by first combining the
Into one sample of size m + n and ranking them from smallest (rank 1) to largest (rank m + n). The test statistic W is then the sum of the ranks of the
B) The Wilcoxon rank-sum interval is very similar to the Wilcoxon signed=rank interval; the later uses pairwise averages from a single sample, whereas the former uses pairwise differences from two samples
C) The Wilcoxon rank-sum interval is quite efficient with respect to the t interval.
D) For large samples, the Wilcoxon rank-sum interval will tend to be only a bit longer than the t interval when the underlying populations are normal, and may be considerably shorter than the t interval if the underlying populations have heavier tails than do normal populations.
E) All of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
53
The accompanying data resulted from an experiment to compare the effects of vitamin C in orange juice and in synthetic ascorbic acid on the length of odontoblasts in guinea pigs over a 6-week period. Use the Wilcoxon rank-sum test at level .01 to decide whether true length differs for the two types of vitamin C intake. Compute also an approximate P-value. 


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
54
A study reports the accompanying data on lead concentration 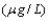 in samples gathered during eight different summer rainfalls: 19.0, 23.4, 32.6, 7.0, 14.2, 13.8, 19.3, and 20.8. Assuming that the lead-content distribution is symmetric, use the Wilcoxon signed-rank interval to obtain a 95% CI for
in samples gathered during eight different summer rainfalls: 19.0, 23.4, 32.6, 7.0, 14.2, 13.8, 19.3, and 20.8. Assuming that the lead-content distribution is symmetric, use the Wilcoxon signed-rank interval to obtain a 95% CI for 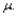
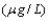 in samples gathered during eight different summer rainfalls: 19.0, 23.4, 32.6, 7.0, 14.2, 13.8, 19.3, and 20.8. Assuming that the lead-content distribution is symmetric, use the Wilcoxon signed-rank interval to obtain a 95% CI for
in samples gathered during eight different summer rainfalls: 19.0, 23.4, 32.6, 7.0, 14.2, 13.8, 19.3, and 20.8. Assuming that the lead-content distribution is symmetric, use the Wilcoxon signed-rank interval to obtain a 95% CI for 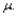

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
55
A Study of Wood reports the following data on burn time (hours) for samples of oak and pine. Test at level .05 to see whether there is any difference in true average burn time for the two types of wood. 


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
56
In an experiment to compare the bond strength of two different adhesives, each adhesive was used in five bondings of two surfaces, and the force necessary to separate the surfaces was determined for each bonding. For adhesive 1, the resulting values were 240, 297, 256, 310, and 261, whereas the adhesive 2 observations were 224, 190, 174, 258, and 236. Let 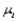 denote the true average bond strength of adhesive type i. Use the Wilcoxon rank-sum test at level .05 to test
denote the true average bond strength of adhesive type i. Use the Wilcoxon rank-sum test at level .05 to test 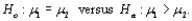
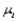 denote the true average bond strength of adhesive type i. Use the Wilcoxon rank-sum test at level .05 to test
denote the true average bond strength of adhesive type i. Use the Wilcoxon rank-sum test at level .05 to test 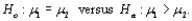

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
57
A sample of 12 radon detectors of a certain type was selected, and each was exposed to 100 pCi/L of radon. The resulting readings were as follows:
109.6 94.9 95.2 100.9 100.5 95.3
105.1 110.0 103.6 111.7 107.3 96.4
Does this data suggest that the population mean reading under these conditions differs from 100? Use the Wilcox test with to test the relevant hypotheses.
to test the relevant hypotheses.
109.6 94.9 95.2 100.9 100.5 95.3
105.1 110.0 103.6 111.7 107.3 96.4
Does this data suggest that the population mean reading under these conditions differs from 100? Use the Wilcox test with
 to test the relevant hypotheses.
to test the relevant hypotheses.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
58
In an experiment designed to study the effects of illumination level on task performance, subjects were required to insert a fine-tipped probe into the eyeholes of ten needles in rapid succession both for a low light level with black background and a higher level with a white background. Each data value is the time (sec) required to complete the task.
Subject Does the data indicate that the higher level of illumination yields a decrease of more than 5 sec in
Does the data indicate that the higher level of illumination yields a decrease of more than 5 sec in
true average task completion time? Test the appropriate hypotheses using the Wilcoxon test.
Subject
 Does the data indicate that the higher level of illumination yields a decrease of more than 5 sec in
Does the data indicate that the higher level of illumination yields a decrease of more than 5 sec intrue average task completion time? Test the appropriate hypotheses using the Wilcoxon test.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
59
Reports are available on a study in which various measurements were taken both from a random sample of infants who had been exposed to household smoke and from a sample of unexposed infants. The accompanying data consists of observations on urinary concentration of cotanine, a major metabolite of nicotine. Does the data suggest that "true" average cotanine level is higher in exposed infants than in unexposed infants by more than 25? Carry out a test at significance level l.05. 


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
60
Which of the following statements are not true?
A) The single-factor ANOVA model for comparing I population or treatment means assumed that for i=1,2,…..,I, a random sample of size
Is drawn from any population with mean
And variance
B) Let
Be the total number of observations in a data set, and suppose we rank all N observations from 1
To N
When
Is false, then some samples will consist mostly of observations having small ranks in the combined sample, whereas others will consist mostly of observations having large ranks.
C) Let
Be the total number of observations in a data set, and suppose we rank all N observations from 1
To N
When
Is true, the N observations all come from the same distribution, in which case all possible assignments of the ranks 1,2,…, N to the J samples are equally likely and we expect ranks to be intermingles in these samples.
D) All of the above statements are true.
E) None of the above statements are true.
A) The single-factor ANOVA model for comparing I population or treatment means assumed that for i=1,2,…..,I, a random sample of size
Is drawn from any population with mean
And variance
B) Let
Be the total number of observations in a data set, and suppose we rank all N observations from 1
To N
When
Is false, then some samples will consist mostly of observations having small ranks in the combined sample, whereas others will consist mostly of observations having large ranks.
C) Let
Be the total number of observations in a data set, and suppose we rank all N observations from 1
To N
When
Is true, the N observations all come from the same distribution, in which case all possible assignments of the ranks 1,2,…, N to the J samples are equally likely and we expect ranks to be intermingles in these samples.
D) All of the above statements are true.
E) None of the above statements are true.

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
61
The accompanying data on cortisol level was reported in a research paper. Experimental subjects were pregnant women whose babies were delivered between 38 and 42 weeks gestation. Group 1 individuals elected to deliver by Caesarean section before labor onset, group 2 delivered by emergency Caesarean during induced labor, and group 3 individuals experienced spontaneous labor. Use the Kruskal-Wallis test at level .05 to test for equality of the three population means. 


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
62
The accompanying data refers to concentration of the radioactive isotope strontium-90 in milk samples obtained from five randomly selected dairies in each of four different regions.  Test at level .10 to see whether true average strontium-90 concentration differs for at least two of the regions.
Test at level .10 to see whether true average strontium-90 concentration differs for at least two of the regions.
 Test at level .10 to see whether true average strontium-90 concentration differs for at least two of the regions.
Test at level .10 to see whether true average strontium-90 concentration differs for at least two of the regions.
Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
63
Compute the 90% rank-sum CI for 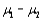 using the following data:
using the following data: 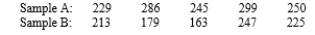
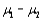 using the following data:
using the following data: 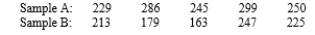

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
64
In a test to determine whether soil pretreated with small amounts of Basic-H makes the soil more permeable to water, soil samples were divided into blocks, and each block received each of the four treatment under study. The treatments were (A) water with .001% Basic-H flooded on control soil, (B) water without Basic-H on control soil, (C) water with Basic-H flooded on soil pretreated with Basic-H, and (D) water without Basic-H on soil pretreated with Basic-H. Test at level .01 to see whether there are any effects due to the different treatments.
Blocks
Blocks


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
65
In an experiment to study the way in which different anesthetics affect plasma epinephrine concentration, ten dogs were selected and concentration was measured while they were under the influence of the anesthetics isoflurane, halothane, and cyclopropane. Test at level .05 to see whether there is an anesthetic effect on concentration.
Dog
Dog


Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
66
Compute a 99% CI for 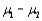 using the following data:
using the following data: 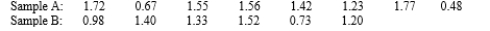
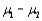 using the following data:
using the following data: 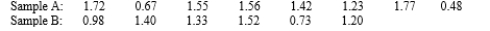

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck



