Deck 5: Probability: an Introduction to Modeling Uncertainty
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/62
Play
Full screen (f)
Deck 5: Probability: an Introduction to Modeling Uncertainty
1
The random variable X is known to be uniformly distributed between 2 and 12. Compute E(X), the expected value of the distribution.
A)4
B)5
C)6
D)7
A)4
B)5
C)6
D)7
7
2
The _______________ probability distribution can be used to estimate the number of vehicles that go through an intersection during the lunch hour.
A)binomial
B)normal
C)triangular
D)Poisson
A)binomial
B)normal
C)triangular
D)Poisson
Poisson
3
The event containing the outcomes belonging to A or B or both is the ________________ of A and B.
A)union
B)Venn diagram
C)intersection
D)subset
A)union
B)Venn diagram
C)intersection
D)subset
union
4
A(n) ________________ is a description of how probabilities are distributed over the values of a random variable.
A)probability distribution
B)mass function of an event
C)density function
D)expected value
A)probability distribution
B)mass function of an event
C)density function
D)expected value

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
5
A joint probability is the
A)sum of the probabilities of two events.
B)probability of the intersection of two events.
C)probability of the union of two events.
D)sum of the probabilities of two independent events.
A)sum of the probabilities of two events.
B)probability of the intersection of two events.
C)probability of the union of two events.
D)sum of the probabilities of two independent events.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
6
The random variable X is known to be uniformly distributed between 2 and 12. Compute the standard deviation of X.
A)2.887
B)3.464
C)8.333
D)12
A)2.887
B)3.464
C)8.333
D)12

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
7
Sample space is
A)a process that results in some outcome.
B)the collection of all possible outcomes.
C)the collection of events
D)a subgroup of a population/the likelihood of an outcome.
A)a process that results in some outcome.
B)the collection of all possible outcomes.
C)the collection of events
D)a subgroup of a population/the likelihood of an outcome.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
8
In the probability table below, which value is a marginal probability? ??
A)0.1
B)1
C)0.5
D)0.4
A)0.1
B)1
C)0.5
D)0.4

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
9
Two events are independent if
A)the two events occur at the same time.
B)the probability of one or both events is greater than 1.
C)the probability of each event is not affected by the other.
D)none of these.
A)the two events occur at the same time.
B)the probability of one or both events is greater than 1.
C)the probability of each event is not affected by the other.
D)none of these.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
10
An initial estimate of the probabilities of events is a ______________ probability.
A)posterior
B)conditional
C)empirical
D)prior
A)posterior
B)conditional
C)empirical
D)prior

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
11
A variable that can only take on specific numeric values is called a
A)categorical variable.
B)discrete random variable.
C)continuous random variable.
A)categorical variable.
B)discrete random variable.
C)continuous random variable.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
12
All the events in the sample space that are not part of the specified event are called
A)joint events.
B)the complement of the event.
C)simple events.
D)independent events.
A)joint events.
B)the complement of the event.
C)simple events.
D)independent events.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
13
If a z-score is zero, then the corresponding x-value must be equal to the
A)mean.
B)median.
C)mode.
D)standard deviation.
A)mean.
B)median.
C)mode.
D)standard deviation.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
14
Probability is the
A)number of successes divided by the number of failures.
B)numerical measure likelihood that an outcome occurs.
C)chance that an event will not happen.
D)number of successes divided by the standard deviation of the distribution.
A)number of successes divided by the number of failures.
B)numerical measure likelihood that an outcome occurs.
C)chance that an event will not happen.
D)number of successes divided by the standard deviation of the distribution.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
15
All of the following are examples of discrete random variables except
A)number of tickets sold.
B)marital status.
C)time.
D)population of a city.
A)number of tickets sold.
B)marital status.
C)time.
D)population of a city.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
16
Which of the following is a discrete random variable?
A)The number of times a student guesses the answers to questions on a certain test.
B)The amount of gasoline purchased by a customer.
C)The amount of mercury found in fish caught in the Gulf of Mexico.
D)The height of water-oak trees.
A)The number of times a student guesses the answers to questions on a certain test.
B)The amount of gasoline purchased by a customer.
C)The amount of mercury found in fish caught in the Gulf of Mexico.
D)The height of water-oak trees.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
17
Which statement is true about mutually exclusive events?
A)If events A and B cannot occur at the same time, they are called mutually exclusive.
B)If either event A or event B must occur, they are called mutually exclusive.
C)P(A) + P(B) = 1 for any events A and B that are mutually exclusive.
D)None of these.
A)If events A and B cannot occur at the same time, they are called mutually exclusive.
B)If either event A or event B must occur, they are called mutually exclusive.
C)P(A) + P(B) = 1 for any events A and B that are mutually exclusive.
D)None of these.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following statements is correct?
A)The binomial and normal distributions are both discrete probability distributions.
B)The binomial and normal distributions are both continuous probability distributions.
C)The binomial distribution is a continuous probability distribution and the normal distribution is a discrete probability distribution.
D)The binomial distribution is a discrete probability distribution and the normal distribution is a continuous probability distribution.
A)The binomial and normal distributions are both discrete probability distributions.
B)The binomial and normal distributions are both continuous probability distributions.
C)The binomial distribution is a continuous probability distribution and the normal distribution is a discrete probability distribution.
D)The binomial distribution is a discrete probability distribution and the normal distribution is a continuous probability distribution.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
19
Bayes' theorem is a method used to compute ___________________ probabilities.
A)posterior
B)conditional
C)empirical
D)prior
A)posterior
B)conditional
C)empirical
D)prior

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
20
An experiment consists of determining the speed of automobiles on a highway by the use of radar equipment. The random variable in this experiment is a
A)discrete random variable.
B)continuous random variable.
C)complex random variable.
D)categorical random variable.
A)discrete random variable.
B)continuous random variable.
C)complex random variable.
D)categorical random variable.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
21
A nickel and a dime are tossed. If an event is defined as a single toss of both coins where at least one head appears, what is the complement of that event?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
22
Fast food restaurants pride themselves in being able to fill orders quickly. A study was done at a local fast food restaurant to determine how long it took customers to receive their order at the drive thru. It was discovered that The time it takes for orders to be filled is exponentially distributed with a mean of 1.5 minutes. What is the probability that it takes less than one minute to fill an order?
A)0.1813
B)0.4866
C)0.6321
D)0.7769
A)0.1813
B)0.4866
C)0.6321
D)0.7769

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
23
The newest model of smart car is supposed to get excellent gas mileage. A thorough study showed that gas mileage (measured in miles per gallon) is normally distributed with a mean of 75 miles per gallon and a standard deviation of 10 miles per gallon. What is the probability that, if driven normally, the car will get 100 miles per gallon or better?
A)0.6%
B)2.5%
C)6%
D)25%
A)0.6%
B)2.5%
C)6%
D)25%

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
24
A nickel and a dime are tossed. How many possible outcomes are in this event?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
25
Fast food restaurants pride themselves in being able to fill orders quickly. A study was done at a local fast food restaurant to determine how long it took customers to receive their order at the drive thru. It was discovered that the time it takes for orders to be filled is exponentially distributed with a mean of 1.5 minutes. What is the probability density function for the time it takes to fill an order? ??
A)
B)?
C)?
D)None of the above answers are correct.
A)
B)?
C)?
D)None of the above answers are correct.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
26
Consider a random experiment of rolling 2 dice. The sample space for rolling two dice is shown. Let S be the set of all ordered pairs listed in the figure. What is probability of rolling a sum larger than 10?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
27
A health conscious student faithfully wears a device that tracks his steps. Suppose that the distribution of the number of steps he takes is normally distributed with a mean of 10,000 and a standard deviation of 1,500 steps. One day he took 15,000 steps. What was his percentile on that day?
A)95%
B)97.7%
C)99.7%
D)100%
A)95%
B)97.7%
C)99.7%
D)100%

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
28
Consider a random experiment of rolling 2 dice. The sample space for rolling two dice is shown. Let S be the set of all ordered pairs listed in the figure. What is probability of rolling a 7?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
29
The center of a normal curve is
A)always equal to zero.
B)the mean of the distribution.
C)always a positive number.
D)equal to the standard deviation.
A)always equal to zero.
B)the mean of the distribution.
C)always a positive number.
D)equal to the standard deviation.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
30
The triangular distribution is a good model for____________ distributions.
A)uniform
B)skewed
C)normal
A)uniform
B)skewed
C)normal

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
31
A nickel and a dime are tossed. We are interested only in the event that includes at least one head appears on a single toss of both coins. What are the possible outcomes?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
32
The newest model of smart car is supposed to get excellent gas mileage. A thorough study showed that gas mileage (measured in miles per gallon) is normally distributed with a mean of 75 miles per gallon and a standard deviation of 10 miles per gallon. What value represents the 50th percentile of this distribution?
A)75
B)85
C)95
D)105
A)75
B)85
C)95
D)105

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
33
A health conscious student faithfully wears a device that tracks his steps. Suppose that the distribution of the number of steps he takes is normally distributed with a mean of 10,000 and a standard deviation of 1,500 steps. How many steps would he have to take to make the cut for the top 5% for his distribution?
A)7,533
B)8,078
C)10,000
D)12,467
A)7,533
B)8,078
C)10,000
D)12,467

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
34
Which of the following is not a characteristic of the normal probability distribution?
A)The mean, median, and the mode are equal.
B)The mean of the distribution can be negative, zero, or positive.
C)The distribution is symmetrical.
D)The standard deviation must be 1.
A)The mean, median, and the mode are equal.
B)The mean of the distribution can be negative, zero, or positive.
C)The distribution is symmetrical.
D)The standard deviation must be 1.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
35
A health conscious student faithfully wears a device that tracks his steps. Suppose that the distribution of the number of steps he takes is normally distributed with a mean of 10,000 and a standard deviation of 1,500 steps. What percent of the time does he exceed 13,000 steps?
A)2.28%
B)5.0%
C)95%
D)97.72%
A)2.28%
B)5.0%
C)95%
D)97.72%

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
36
James has two fair coins. When he flips them, what is the sample space?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
37
What is the mean of x, given the exponential probability function
A)0.05
B)20
C)100
D)2,000
A)0.05
B)20
C)100
D)2,000

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
38
What is the total area under the normal distribution curve?
A)It depends upon the mean and standard deviation
B)It must be calculated
C)1
D)100
A)It depends upon the mean and standard deviation
B)It must be calculated
C)1
D)100

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
39
Consider a random experiment of rolling 2 dice. The sample space for rolling two dice is shown. Let S be the set of all ordered pairs listed in the figure. What are the possible outcomes for the event of rolling a 7?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
40
In a normal distribution, which is greater, the mean or the median?
A)Mean
B)Median
C)Neither (they are equal)
D)Cannot be determined with the information provided
A)Mean
B)Median
C)Neither (they are equal)
D)Cannot be determined with the information provided

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
41
Given that A and B are independent with P(A ∪ B) = 0.8 and P(Bc) = 0.3, find P(A).

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
42
What type of distribution models the number of occurrences of an event over a specified interval of time or space?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
43
The contingency table below represents employees of a communications company classified by age and field of expertise. Fill in the missing entries.
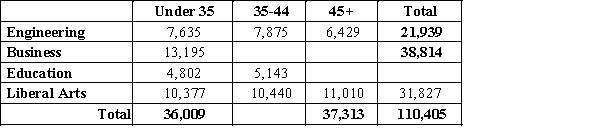


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
44
A bucket contains 2 red balls, 4 yellow balls, and 5 purple balls. One ball is taken from the bucket and then replaced. Another ball is taken from the bucket. What is the probability that the first ball is red and the second ball is purple?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
45
The cross tabulation below classifies employees of a communications company by age and field of expertise. Use the given information to create a joint probability table.
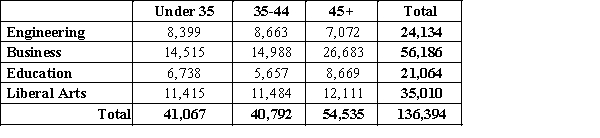


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
46
Participants at the state fair were given 8 rings to toss. The number x of rings tossed onto a stick can be approximated by the probability distribution in the table. Use the probability distribution to find the mean and variance of the probability distribution.



Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
47
The random variable X is known to be uniformly distributed between 2 and 12. Compute P(X = 3).

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
48
Could this curve represent a normal distribution?
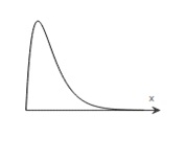


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
49
The contingency table below represents employees of a communications company classified by age and field of expertise. What is the probability that a randomly selected employee age 35-45 years old has business expertise?
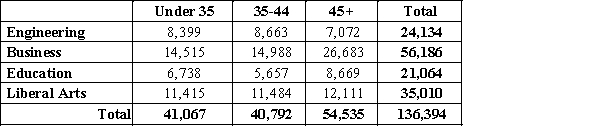


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
50
In a binomial experiment, what does it mean to say that each trial is independent of the other trials?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
51
You recently took a standardized test in which scores follow a normal distribution with a mean of 18 and a standard deviation of 3. You were told that your score is at the 75th percentile of this distribution. What is your score?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
52
For the standard normal probability distribution, what percent of the curve lies to the left of the mean?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
53
The cross tabulation shown below shows employees of a communications company classified by age and field of expertise. What is the probability that a randomly selected engineer is under the age of 35?
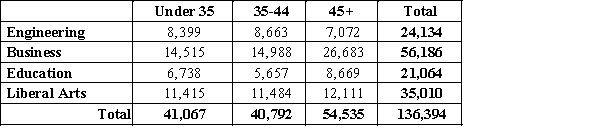


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
54
Given that P(A) = 0.3, P(A|B) = 0.4, and P(B) = 0.5, compute P(A ∩ B)

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
55
Let X be a random variable with a Uniform distribution between 8 and 20. Find the probability that X is less than 10?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
56
The time in seconds that it takes a production worker to inspect an item has an exponential distribution with mean 15 seconds. What proportion of inspection times is less than 10 seconds?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
57
A bucket contains 2 red balls, 4 yellow balls, and 5 purple balls. One ball is taken from the bucket and then replaced. Another ball is taken from the bucket. Are the events of pulling first ball is red then a purple one independent or dependent?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
58
The random variable X is known to be uniformly distributed between 2 and 12. Compute P(X > 10).

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
59
A bucket contains 3 red balls, 4 yellow balls, and 5 purple balls. One ball is taken from the bucket and is not replaced. Another ball is taken from the bucket. What is the probability that the first ball is red and the second ball is purple?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
60
A bucket contains 3 red balls, 4 yellow balls, and 5 purple balls. One ball is taken from the bucket and is not replaced. Another ball is taken from the bucket. Are the events of pulling first ball is red then a purple one independent or dependent?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
61
Reviews of call center representatives over the last 3 years showed that 10% of all call center representatives were rated as outstanding, 75% were rated as excellent/good, 10% percent were rated as satisfactory, and 5% were considered unsatisfactory. For a sample of 10 reps selected at random, what is the probability that two will be rated as unsatisfactory?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
62
The random variable X is normally distributed with mean of 80 and standard deviation of 10. What is the probability that a value of X chosen at random will be between 70 and 90?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck



