Deck 14: Amortization of Loans, Residential Mortgages, and Sinking Funds
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/132
Play
Full screen (f)
Deck 14: Amortization of Loans, Residential Mortgages, and Sinking Funds
1
Cody borrowed $9100.00 from his credit union. He agreed to repay the loan by making equal monthly payments for 4 years. Interest is 9% compounded monthly.
a)What is the size of the monthly payments?
b)How much will the loan cost him?
c)How much will Cody owe after 16 months?
d)How much interest will he pay in his 26th payment?
e)How much of the principal will be repaid in the 18th payment?
f)Prepare a partial amortization schedule showing details of the first three payments, Payments 24, 25, 26, the last three payments, and totals.
a)What is the size of the monthly payments?
b)How much will the loan cost him?
c)How much will Cody owe after 16 months?
d)How much interest will he pay in his 26th payment?
e)How much of the principal will be repaid in the 18th payment?
f)Prepare a partial amortization schedule showing details of the first three payments, Payments 24, 25, 26, the last three payments, and totals.
 Partial Amortization Table (each step rounded to the nearest cent).
Partial Amortization Table (each step rounded to the nearest cent). 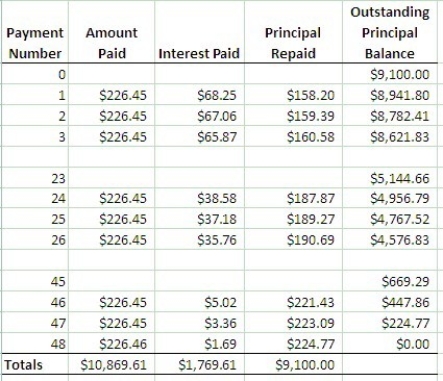
2
A $30 000.00 mortgage is amortized by monthly payments over twenty years and is renewable after five years.
a)If the interest rate is 8.5% compounded semi-annually, calculate the outstanding balance at the end of the five-year term.
b)If the mortgage is renewed for a further three-year term at 8% compounded semi-annually, calculate the size of the new monthly payment.
c)Calculate the payout figure at the end of the three-year term.
a)If the interest rate is 8.5% compounded semi-annually, calculate the outstanding balance at the end of the five-year term.
b)If the mortgage is renewed for a further three-year term at 8% compounded semi-annually, calculate the size of the new monthly payment.
c)Calculate the payout figure at the end of the three-year term.
a)PV = 30 000.00; n = 20(12)= 240; i = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e4_935a_e9d3f971aa05_TB4212_11.jpg) = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c =
= 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e5_935a_cf436883b16a_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e6_935a_b1f08d4edd6c_TB4212_11.jpg) p =
p = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e7_935a_a15b3d7296dc_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e8_935a_97ea6141df66_TB4212_11.jpg) - 1 = 0.006961062
- 1 = 0.006961062
30000 = PMT![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e9_935a_090e43e54d94_TB4212_00.jpg) 30000 = PMT[116.4742048]
30000 = PMT[116.4742048]
PMT = $257.57
The number of outstanding payments after five years is 15(12)= 180
PV = 257.57![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0ea_935a_b7c7456772df_TB4212_00.jpg) PV = $26 386.10
PV = $26 386.10
Programmed solution:![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fb_935a_71d447a35a07_TB4212_00.jpg)
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fc_935a_955962501cff_TB4212_00.jpg) b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years.
b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years.
PV = 26 386.10; n = 15(12)= 180; i =![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fd_935a_bd6ade38a761_TB4212_11.jpg) = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c =
= 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fe_935a_9b3b0ad3f22a_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7ff_935a_7ff835995bf4_TB4212_11.jpg) p =
p = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f800_935a_b77f91f4f719_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f801_935a_afa715093d0b_TB4212_11.jpg) - 1 = 0.006558197
- 1 = 0.006558197
26386.10 = PMT![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f802_935a_3133ae4d0609_TB4212_11.jpg) 26386.10 = PMT[105.4682161]
26386.10 = PMT[105.4682161]
PMT = $250.18
Programmed solution:![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f803_935a_33027cefd487_TB4212_00.jpg) c)At the end of the 3 year term the outstanding payments is 144.
c)At the end of the 3 year term the outstanding payments is 144.
PV = 250.18![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f804_935a_d1e029cb5d6f_TB4212_00.jpg) PV = $23 265.45
PV = $23 265.45
Programmed solution:![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f805_935a_9908e346ff90_TB4212_00.jpg)
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e4_935a_e9d3f971aa05_TB4212_11.jpg) = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c =
= 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e5_935a_cf436883b16a_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e6_935a_b1f08d4edd6c_TB4212_11.jpg) p =
p = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e7_935a_a15b3d7296dc_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e8_935a_97ea6141df66_TB4212_11.jpg) - 1 = 0.006961062
- 1 = 0.00696106230000 = PMT
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0e9_935a_090e43e54d94_TB4212_00.jpg) 30000 = PMT[116.4742048]
30000 = PMT[116.4742048]PMT = $257.57
The number of outstanding payments after five years is 15(12)= 180
PV = 257.57
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_d0ea_935a_b7c7456772df_TB4212_00.jpg) PV = $26 386.10
PV = $26 386.10Programmed solution:
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fb_935a_71d447a35a07_TB4212_00.jpg)
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fc_935a_955962501cff_TB4212_00.jpg) b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years.
b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years.PV = 26 386.10; n = 15(12)= 180; i =
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fd_935a_bd6ade38a761_TB4212_11.jpg) = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c =
= 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7fe_935a_9b3b0ad3f22a_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f7ff_935a_7ff835995bf4_TB4212_11.jpg) p =
p = ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f800_935a_b77f91f4f719_TB4212_11.jpg) =
= ![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f801_935a_afa715093d0b_TB4212_11.jpg) - 1 = 0.006558197
- 1 = 0.00655819726386.10 = PMT
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f802_935a_3133ae4d0609_TB4212_11.jpg) 26386.10 = PMT[105.4682161]
26386.10 = PMT[105.4682161]PMT = $250.18
Programmed solution:
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f803_935a_33027cefd487_TB4212_00.jpg) c)At the end of the 3 year term the outstanding payments is 144.
c)At the end of the 3 year term the outstanding payments is 144.PV = 250.18
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f804_935a_d1e029cb5d6f_TB4212_00.jpg) PV = $23 265.45
PV = $23 265.45Programmed solution:
![a)PV = 30 000.00; n = 20(12)= 240; i = = 0.0425; I/Y = 8.5; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006961062 30000 = PMT 30000 = PMT[116.4742048] PMT = $257.57 The number of outstanding payments after five years is 15(12)= 180 PV = 257.57 PV = $26 386.10 Programmed solution: b)The outstanding balance of $26 386.10 is to be amortized the remaining 15 years. PV = 26 386.10; n = 15(12)= 180; i = = 0.04; I/Y = 8; P/Y = 12; C/Y = 2; c = = p = = - 1 = 0.006558197 26386.10 = PMT 26386.10 = PMT[105.4682161] PMT = $250.18 Programmed solution: c)At the end of the 3 year term the outstanding payments is 144. PV = 250.18 PV = $23 265.45 Programmed solution:](https://d2lvgg3v3hfg70.cloudfront.net/TB4212/11eb129f_900a_f805_935a_9908e346ff90_TB4212_00.jpg)
3
A loan of $8380.00 is repaid by equal payments made at the end of every three months for 3 years. If interest is 7% compounded quarterly, find the size of the quarterly payments and construct an amortization schedule showing the total paid and the total cost of the loan.
8380.00 = PMT 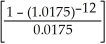 8380.00 = PMT(10.7395497)
8380.00 = PMT(10.7395497)
$780.29 = PMT
Amortization Schedule (done using Excel):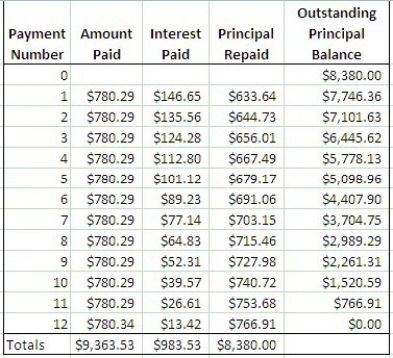
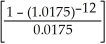 8380.00 = PMT(10.7395497)
8380.00 = PMT(10.7395497)$780.29 = PMT
Amortization Schedule (done using Excel):

4
Rola Inc. borrowed $42 000.00 at 7% compounded semi-annually. The loan is repaid by payments of $4700.00 due at the end of every six months.
a)How many payments are needed?
b)How much of the principal will be repaid by the 6th payment?
c)Prepare a partial amortization schedule showing the details of the last three payments and totals.
a)How many payments are needed?
b)How much of the principal will be repaid by the 6th payment?
c)Prepare a partial amortization schedule showing the details of the last three payments and totals.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
5
A debt of $10 000.00 with interest at 8% compounded quarterly is to be repaid by equal payments at the end of every three months for two years.
a)Calculate the size of the monthly payments.
b)Construct an amortization table.
c)Calculate the outstanding balance after three payments.
a)Calculate the size of the monthly payments.
b)Construct an amortization table.
c)Calculate the outstanding balance after three payments.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
6
Barbara borrowed $12 000.00 from the bank at 9% compounded monthly. The loan is amortized with end-of-month payments over five years.
a)Calculate the interest included in the 20th payment.
b)Calculate the principal repaid in the 36th payment.
c)Construct a partial amortization schedule showing the details of the first two payments, the 20th payment, the 36th payment, and the last two payments.
d)Calculate the totals of amount paid, interest paid, and the principal repaid.
a)Calculate the interest included in the 20th payment.
b)Calculate the principal repaid in the 36th payment.
c)Construct a partial amortization schedule showing the details of the first two payments, the 20th payment, the 36th payment, and the last two payments.
d)Calculate the totals of amount paid, interest paid, and the principal repaid.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
7
A debt of $12 970.00 with interest at 7.23% compounded semi-annually is repaid by payments of $1880.00 made at the end of every three months. Construct an amortization schedule showing the total paid and the total cost of the debt.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
8
A investor's price for a townhouse was $160 000.00. Sepaba Investments., the buyers of the rental unit, paid $40 000.00 down and financed the balance by making equal payments at the end of every six months for 25 years. Interest is 6% compounded semi-annually.
a)What is the size of the semi-annual payment?
b)How much will Sepaba Investments. owe after 20 years?
c)What is the total cost of the building for Sepaba Investments?
d)What is the total interest included in the payments?
a)What is the size of the semi-annual payment?
b)How much will Sepaba Investments. owe after 20 years?
c)What is the total cost of the building for Sepaba Investments?
d)What is the total interest included in the payments?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
9
The Taylors agreed to monthly payments rounded up to the nearest $100.00 on a mortgage of $136 000.00 amortized over 15 years. Interest for the first five years was 8.5% compounded semi-annually. After 30 months, as permitted by the mortgage agreement, the Taylors increased the rounded monthly payment by 10%.
a)Determine the mortgage balance at the end of the five-year term.
b)If the interest rate remains unchanged over the remaining term, how many more of the increased payments will amortize the mortgage balance?
c)How much did the Taylors save by exercising the increase-in-payment option?
a)Determine the mortgage balance at the end of the five-year term.
b)If the interest rate remains unchanged over the remaining term, how many more of the increased payments will amortize the mortgage balance?
c)How much did the Taylors save by exercising the increase-in-payment option?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
10
Olfert Inc. is repaying a loan of $52 500.00 by making payments of $4700.00 at the end of every six months. If interest is 7.5% compounded semi-annually, construct an amortization schedule showing the total paid and the total cost of the loan.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
11
The owner of the Pink Flamingo Motel borrowed $19 500.00 at 8.11% compounded semi-annually and agreed to repay the loan by making payments of $1110.00 at the end of every three months.
a)How many payments will be needed to repay the loan?
b)How much will be owed at the end of five years?
c)How much of the payments made at the end of five years will be interest?
a)How many payments will be needed to repay the loan?
b)How much will be owed at the end of five years?
c)How much of the payments made at the end of five years will be interest?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
12
A contractor's price for a new building was $85 100.00. Stampede Inc., the buyers of the building, paid $14 000.00 down and financed the balance by making equal payments at the end of every six months for 14 years. Interest is 12% compounded semi-annually.
a)What is the size of the semi-annual payment?
b)How much will Stampede Inc. owe after 6 years?
c)What is the total cost of the building for Stampede Inc.?
d)What is the total interest included in the payments?
a)What is the size of the semi-annual payment?
b)How much will Stampede Inc. owe after 6 years?
c)What is the total cost of the building for Stampede Inc.?
d)What is the total interest included in the payments?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
13
Mr. Lamb borrowed $8321.00 at 11.12% compounded monthly. He agreed to repay the loan in equal monthly payments over five years.
a)What is the size of the monthly payment?
b)How much of the 24th payment is interest?
c)What is the principal repaid in the 37th payment?
d)Prepare a partial amortization schedule showing details of the first three payments, the last three payments, and totals.
a)What is the size of the monthly payment?
b)How much of the 24th payment is interest?
c)What is the principal repaid in the 37th payment?
d)Prepare a partial amortization schedule showing details of the first three payments, the last three payments, and totals.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
14
A loan of $19 000.00 is repaid by quarterly payments of $900.00 each at 8% compounded quarterly. What is the principal repaid by the 21st payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
15
A loan of $14 100.00 is amortized over 11 years by equal monthly payments at 5.4% compounded monthly. Construct an amortization schedule showing details of the first three payments, the fortieth payment, the last three payments, and totals.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
16
Vicki receives payments of $3000.00 at the beginning of each month from a pension fund of $150 000.00. Interest earned by the fund is 6% compounded monthly. What is the number of payments Vicki will receive?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
17
Sean and friends bought a property valued at $50 000 for $5000.00 down and a mortgage amortized over 10 years. The group makes equal payments due at the end of every three months. Interest on the mortgage is 6.00% compounded annually and the mortgage is renewable after five years.
a)What is the size of each quarterly payment?
b)What is the outstanding principal at the end of the five-year term?
c)What is the cost of the mortgage for the first five years?
d)If the mortgage is renewed for a further five years at 9% compounded semi-annually, what will be the size of each quarterly payment?
a)What is the size of each quarterly payment?
b)What is the outstanding principal at the end of the five-year term?
c)What is the cost of the mortgage for the first five years?
d)If the mortgage is renewed for a further five years at 9% compounded semi-annually, what will be the size of each quarterly payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
18
A loan of $10 000.00 is repaid by quarterly payments of $1000.00 each at 12% compounded quarterly. What is the principal repaid by the 11th payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
19
A debt of $12 500.00 with interest at 5.5% compounded semi-annually is amortized by making payments of $1000.00 at the end of every six months. Calculate the outstanding balance after five years.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
20
Duguid and Partners bought a property valued at $87 300.00 for $17 000.00 down and a mortgage amortized over 17 years. The firm makes equal payments due at the end of every three months. Interest on the mortgage is 6.85% compounded annually and the mortgage is renewable after five years.
a)What is the size of each quarterly payment?
b)What is the outstanding principal at the end of the five-year term?
c)What is the cost of the mortgage for the first five years?
d)If the mortgage is renewed for a further five years at 7.17% compounded semi-annually, what will be the size of each quarterly payment?
a)What is the size of each quarterly payment?
b)What is the outstanding principal at the end of the five-year term?
c)What is the cost of the mortgage for the first five years?
d)If the mortgage is renewed for a further five years at 7.17% compounded semi-annually, what will be the size of each quarterly payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
21
Catrina receives payments of $1120.00 at the beginning of each month from a pension fund of $79 500.00. Interest earned by the fund is 11.36% compounded monthly.
a)What is the number of payments Catrina will receive?
b)What is the size of the final payment?
a)What is the number of payments Catrina will receive?
b)What is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
22
Angelina has agreed to purchase her partner's share in the business by making payments of $1720.00 every three months. The agreed transfer value is $19 500.00 and interest is 9.11% compounded annually. If the first payment is due at the date of the agreement, what is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
23
A $248 000.00 mortgage amortized by monthly payments over 35 years is renewable after five years. Interest is 8.12% compounded semi-annually.
a)What is the size of the monthly payments?
b)How much interest is paid during the first year?
c)How much of the principal is repaid during the first five-year term?
d)If the mortgage is renewed for a further five-year term at 7.16% compounded semi-annually, what will be the size of the monthly payments?
a)What is the size of the monthly payments?
b)How much interest is paid during the first year?
c)How much of the principal is repaid during the first five-year term?
d)If the mortgage is renewed for a further five-year term at 7.16% compounded semi-annually, what will be the size of the monthly payments?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
24
A $180 000.00 mortgage is to be amortized by making monthly payments for 22.5 years. Interest is 7.2% compounded semi-annually for a four-year term.
a)Compute the size of the monthly payment.
b)Determine the balance at the end of the four-year term.
c)If the mortgage is renewed for a five-year term at 8.66% compounded semi-annually, what is the size of the monthly payment for the renewal term?
a)Compute the size of the monthly payment.
b)Determine the balance at the end of the four-year term.
c)If the mortgage is renewed for a five-year term at 8.66% compounded semi-annually, what is the size of the monthly payment for the renewal term?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
25
A debt of $42 500.00 is repaid by payments of $4850.00 made at the end of each year. Interest is 7% compounded semi-annually.
a)How many payments are needed to repay the debt?
b)What is the cost of the debt for the first three years?
c)What is the principal repaid in the 3rd year?
d)Construct an amortization schedule showing details of the first three payments, the last three payments, and totals.
a)How many payments are needed to repay the debt?
b)What is the cost of the debt for the first three years?
c)What is the principal repaid in the 3rd year?
d)Construct an amortization schedule showing details of the first three payments, the last three payments, and totals.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
26
A contract worth $59 000.00 provides benefits of $21 000.00 at the end of each year. The benefits are deferred for six years and interest is 8.95% compounded quarterly.
a)How many payments are to be made under the contract?
b)What is the size of the last benefit payment?
a)How many payments are to be made under the contract?
b)What is the size of the last benefit payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
27
Payments of $1000.00 deferred for nine years are received at the end of each month from a fund of $20 000.00 deposited today at 6% compounded monthly. Calculate the size of the final payment.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
28
A contract valued at $47 500.00 requires payments of $6951.00 every six months. The first payment is due in four years and interest is 6.6% compounded semi-annually.
a)How many payments are required?
b)What is the size of the last payment?
c)How much will be paid in total?
d)How much of what is paid is interest?
a)How many payments are required?
b)What is the size of the last payment?
c)How much will be paid in total?
d)How much of what is paid is interest?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
29
The owner of the Guelph Inc. borrowed $20 000.00 at 1.2% compounded semi-annually and agreed to repay the loan by making payments of $1000.00 at the end of every three months.
a)How many payments will be needed to repay the loan?
b)How much will be owed at the end of five years?
a)How many payments will be needed to repay the loan?
b)How much will be owed at the end of five years?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
30
Far East Imports Inc. owes $64 000.00 to be repaid by monthly payments of $2475.00. Interest is 6.12% compounded monthly.
a)How many payments will Far East Imports Inc. have to make?
b)How much interest is included in the 15th payment?
c)How much of the principal will be repaid by the 17th payment?
d)Construct a partial amortization schedule showing details of the first three payments, the last three payments, and totals.
a)How many payments will Far East Imports Inc. have to make?
b)How much interest is included in the 15th payment?
c)How much of the principal will be repaid by the 17th payment?
d)Construct a partial amortization schedule showing details of the first three payments, the last three payments, and totals.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
31
A factory valued at $100 000.00 is purchased for a down payment of 28% and payments of $4000.00 at the end of every three months. If interest is 9% compounded monthly, calculate the size of the final payment.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
32
A mortgage balance of $137 960.70 is to be repaid over a eleven-year term by equal monthly payments at 8.1% compounded semi-annually. At the request of the mortgagor, the monthly payments were set at $1140.00.
a)How many payments will the mortgagor have to make?
b)What is the size of last payment?
c)Determine the difference between the total actual amount paid and the total amount required to amortize the mortgage by the contractual monthly payments.
a)How many payments will the mortgagor have to make?
b)What is the size of last payment?
c)Determine the difference between the total actual amount paid and the total amount required to amortize the mortgage by the contractual monthly payments.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
33
Lisa saved $750 000.00. If she withdraws $12 000.00 at the beginning of every month and interest is 12% compounded monthly, what is the size of the last withdrawal?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
34
A debt of $43 100.00 is repaid by payments of $3350.00 made at the end of every six months. Interest is 8.4% compounded quarterly.
a)What is the number of payments needed to retire the debt?
b)What is the cost of the debt for the first five years?
c)What is the interest paid in the 11th payment?
d)Construct a partial amortization schedule showing details of the first three payments, the last three payments, and totals.
a)What is the number of payments needed to retire the debt?
b)What is the cost of the debt for the first five years?
c)What is the interest paid in the 11th payment?
d)Construct a partial amortization schedule showing details of the first three payments, the last three payments, and totals.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
35
A debt of $41 000.00 is repaid in monthly installments of $660.00. If interest is 8.4% compounded quarterly, what is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
36
Tom receives pension payments of $6000.00 at the end of every six months from a retirement fund of $90 000.00. The fund earns 8.00% compounded semi-annually.
a)How many payments will Tom receive?
b)What is the size of the final pension payment?
a)How many payments will Tom receive?
b)What is the size of the final pension payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
37
A debt of $40 000.00 is repaid in monthly installments of $500.00. If interest is 8.0% compounded quarterly, what is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
38
Andre has saved $152 000.00. If he withdraws $1750.00 at the beginning of every month and interest is 7.5% compounded monthly, what is the size of the last withdrawal?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
39
John has agreed to purchase his partner's share in real estate by making payments of $5000.00 every three months. The agreed transfer value is $40 000.00 and interest is 10% compounded annually. If the first payment is due at the date of the agreement, what is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
40
Karen receives pension payments of $4570.00 at the end of every six months from a retirement fund of $82 000.00. The fund earns 8.06% compounded semi-annually.
a)How many payments will Karen receive?
b)What is the size of the final pension payment?
a)How many payments will Karen receive?
b)What is the size of the final pension payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
41
What is the size of the final unequal payment of a loan for $2723.44 if it has quarterly payments of $500? The interest rate is 8.4% compounded quarterly.
A)$432.14
B)$423.14
C)$441.14
D)$414.14
E)$424.14
A)$432.14
B)$423.14
C)$441.14
D)$414.14
E)$424.14

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
42
A $151 000.00 mortgage is to be repaid over a 17-year period by monthly payments rounded up to the next higher $50.00. Interest is 8.2% compounded semi-annually.
a)Determine the number of rounded payments required to repay the mortgage.
b)Determine the size of the last payment.
c)Calculate the amount of interest saved by rounding the payments up to the next higher $50.00.
a)Determine the number of rounded payments required to repay the mortgage.
b)Determine the size of the last payment.
c)Calculate the amount of interest saved by rounding the payments up to the next higher $50.00.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
43
How much principal is repaid in the 74th payment interval on a $142 300 mortgage? The mortgage is amortized over 25 years and the payments are monthly. The interest rate is 7.44% compounded monthly.
A)$257.16
B)$275.16
C)$527.16
D)$572.16
E)$574.16
A)$257.16
B)$275.16
C)$527.16
D)$572.16
E)$574.16

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
44
The Acme Parts Company is repaying a debt of $15 000.00 by payments of $1410.00 made at the end of every three months. Interest is 7.2% compounded monthly.
a)How many payments are needed to repay the debt?
b)What is the size of the final payment?
a)How many payments are needed to repay the debt?
b)What is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
45
What is the monthly payment size of a 25-year mortgage for $100 000 and an interest rate of 6% compounded semi-annually?
A)$639.81
B)$1639.81
C)$630.81
D)$600.81
E)633.81
A)$639.81
B)$1639.81
C)$630.81
D)$600.81
E)633.81

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
46
What is the outstanding balance after the 23rd payment interval of a 16-year loan for $14 734 with semi-annual payments and an interest rate of 5.95% compounded quarterly?
A)$5625.21
B)$5652.21
C)$5562.21
D)$5526.21
E)$5566.21
A)$5625.21
B)$5652.21
C)$5562.21
D)$5526.21
E)$5566.21

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
47
A bank has an interest rate of 5% compounded semi annually for a five year closed mortgage. If the mortgage has monthly payments, calculate the effective rate of interest per each term.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
48
How much total interest is paid between the 6th and 13th payments on a loan that has monthly payments for 3 years and an original principal of $14 750? The loan rate is 6.6% compounded quarterly.
A)$540
B)$405
C)$450
D)$504
E)$545
A)$540
B)$405
C)$450
D)$504
E)$545

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
49
A $176 000.00 mortgage is to be repaid over a 21-year period by monthly payments rounded up to the next higher $100.00. Interest is 9.44% compounded semi-annually.
a)Determine the number of rounded payments required to repay the mortgage.
b)Determine the size of the last payment.
a)Determine the number of rounded payments required to repay the mortgage.
b)Determine the size of the last payment.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
50
Munawar is a first time buyer and bought a brand new townhouse in Oshawa for $212 000. He has saved enough to make a 5% down payment and will have to pay mortgage loan insurance at 2.75% of the mortgage balance. Munawar wants the insurance premium added to the maximum allowable loan balance. Determine his maximum initial mortgage balance.
A)$5538.50
B)$201 400
C)$206 938.50
D)$212 000
E)$212 477
A)$5538.50
B)$201 400
C)$206 938.50
D)$212 000
E)$212 477

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
51
What is the size of the final unequal payment of a loan that has 69.47 payments and the equal payment size is $215.64? The interest rate is 3.1% per compounding period.
A)$120.17
B)$210.17
C)$102.17
D)$99.10
E)$99.17
A)$120.17
B)$210.17
C)$102.17
D)$99.10
E)$99.17

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
52
How much interest is paid after the first payment interval on a $100 000 mortgage? The mortgage is amortized over 25 years and the payments are monthly. The interest rate is 6% compounded semi-annually. Round your answer to the nearest dollar.
A)$146
B)$640
C)$527
D)$494
E)$401
A)$146
B)$640
C)$527
D)$494
E)$401

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
53
How much total principal is repaid between the 1st and 7th payment interval of a 4.5-year loan for $4887 at an interest rate of 7.4% compounded monthly and the payments are also monthly. Round your answer to the nearest dollar.
A)$556
B)$546
C)$456
D)$445
E)$423
A)$556
B)$546
C)$456
D)$445
E)$423

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
54
How much interest is paid in total on a 3-year loan for $28 600 (rounded to the nearest dollar)? The interest rate is 8.7% compounded monthly and the payments are monthly.
A)$3997
B)$3779
C)$3977
D)$3999
E)$4000
A)$3997
B)$3779
C)$3977
D)$3999
E)$4000

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
55
How much interest is paid in the 53rd monthly payment interval of a loan for $43 200? The loan is amortized at a rate of 9.17% compounded annually over 7 years.
A)$411.11
B)$111.11
C)$144.11
D)$444.11
E)$400.11
A)$411.11
B)$111.11
C)$144.11
D)$444.11
E)$400.11

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
56
How much interest is paid in total on a 1-year loan for $5000? The interest rate is 12 % compounded monthly and the payments are monthly.
A)$330.00
B)$333.88
C)$333.00
D)$300.88
E)$330.88
A)$330.00
B)$333.88
C)$333.00
D)$300.88
E)$330.88

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
57
A demand (variable rate)mortgage of $137 000.00 is amortized over 20 years by equal monthly payments. After 21 months the original interest rate of 6% p.a was raised to 6.6% p.a. Three years after the mortgage was taken out, it was renewed at the request for the mortgagor for a five-year term at a fixed rate of 7.25% p.a.
a)Calculate the mortgage balance after 21 months.
b)Compute the size of the new monthly payment at the 6.6% rate of interest.
c)Determine the mortgage balance at the end of the five-year term.
a)Calculate the mortgage balance after 21 months.
b)Compute the size of the new monthly payment at the 6.6% rate of interest.
c)Determine the mortgage balance at the end of the five-year term.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
58
What is the monthly payment size of a 21-year mortgage for $169 600 and an interest rate of 7.2% compounded semi-annually?
A)$1169.11
B)$1296.11
C)$1926.11
D)$1211.96
E)$1222.96
A)$1169.11
B)$1296.11
C)$1926.11
D)$1211.96
E)$1222.96

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
59
A debt of $17 000.00 is repaid by quarterly payments of $1430.00. If interest is 6.12% compounded quarterly, what is the size of the final payment?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
60
What is the outstanding balance after 23 payments on a 20-year mortgage that has monthly payments of $1062.32 and an interest rate of 6.6% compounded monthly?
A)$143 402.54
B)$144 302.54
C)$134 402.54
D)$134 302.54
E)$134 322.54
A)$143 402.54
B)$144 302.54
C)$134 402.54
D)$134 302.54
E)$134 322.54

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
61
Li bought a house in Whitby for $305 000 5 years ago. He financed the house through Scotia Bank with a mortgage of $259 000 amortized over 25 years. Interest for the first 5 years was 4.4% compounded semi-annually and payments were made monthly. At the end of the 5 year term, Li has renewed the mortgage for another 5 years, at 3.7% compounded semi-annually. What is the monthly payment for the second term?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
62
Tariq bought a commercial property valued at $130 000 for $26 000.00 down and a mortgage amortized over 25 years. He makes equal payments due at the end of every month. Interest on the mortgage is 4.1% compounded semi-annually and the mortgage is renewable after five years. What is the cost of the mortgage for the first five years?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
63
Zara bought a 2013 Kia Forte by taking a $19 500 loan from BMO with interest at 5.99% compounded annually and amortized by payments of $378 at the end of every month. She receives an inheritance after making 36 payments and plans to pay the balance in full. What is the payout figure just after the last regular payment made?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
64
A car loan of $46 700.00 is amortized over 8 years by equal monthly payments at 2.9% compounded monthly. What is the monthly payment and outstanding principal balance after 40 payments.
A)$545.66 and $28 546.88
B)$545.66 and $18 153.12
C)$544.34 and $28,478.06
D)$486.46 and $27 241.67
A)$545.66 and $28 546.88
B)$545.66 and $18 153.12
C)$544.34 and $28,478.06
D)$486.46 and $27 241.67

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
65
Zam Zam Inc. borrowed $142 000.00 at 4.4% compounded semi-annually. The loan is repaid by payments of $9700.00 due at the end of every six months. How many payments are needed and what will be the outstanding balance after 8 payments?
A)18 and $85 158
B)18 and $81 520
C)18 and $60 480
D)18 and $56 842
E)15 and $64 800
A)18 and $85 158
B)18 and $81 520
C)18 and $60 480
D)18 and $56 842
E)15 and $64 800

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
66
Big Printing Inc. is repaying a loan of $37 300.00 by making payments of $2300.00 at the end of every three months. If interest is 3.5% compounded quarterly, construct an amortization schedule showing the total paid and the total cost of the loan. What is the total interest paid and cost of the loan?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
67
The owner of the Pink Flamingo Motel borrowed $19 500.00 at 8.11% compounded semi-annually and agreed to repay the loan by making payments of $1110.00 at the end of every three months.
a)How many payments will be needed to repay the loan?
b)How much will be owed at the end of five years?
c)How much of the payments made at the end of five years will be interest?
a)How many payments will be needed to repay the loan?
b)How much will be owed at the end of five years?
c)How much of the payments made at the end of five years will be interest?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
68
Shiva transferred his mortgage of $145 981 from CIBC to BMO for the remaining amortization period at 3.59% compounded semi-annually. He has agreed to pay rounded up payment of $2000 every month. How long will it take Shiva to pay-off his mortgage?
A)6 years 11 months
B)6 years 1 months
C)8 years
D)6 years 6 months
E)10 years
A)6 years 11 months
B)6 years 1 months
C)8 years
D)6 years 6 months
E)10 years

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
69
Keith receives payments of $14 500.00 at the beginning of each month from a pension fund of $1 500 000.00. Interest earned by the fund is 7.6% compounded monthly. What is the number of payments Keith will receive?
A)167
B)169
C)156
D)140
E)104
A)167
B)169
C)156
D)140
E)104

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
70
Rebecca borrowed $20 400 from her local credit union to pay for the upgrades in her kitchen. She wants to pay the loan with monthly payments over the period of 3 years. What is the interest included in the tenth payment, if the rate charged by the credit union is 6% monthly?
A)$78.19
B)$5698.49
C)$21 336.56
D)$15 638.09
E)$75.48
A)$78.19
B)$5698.49
C)$21 336.56
D)$15 638.09
E)$75.48

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
71
The Korean community is planning to buy a place for their community in Markham valued at $1 697 000. They made a down payment of 10% and payments of $400 000 are required at the end of every 3 months. If interest is 9% compounded monthly, what is the size of the final payment
A)$15 685
B)$205 512
C)$131 373
D)$355 547
E)$48 381
A)$15 685
B)$205 512
C)$131 373
D)$355 547
E)$48 381

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
72
Amanda borrowed $57 800 from BMO to buy a 2014 E-Class Mercedes Sedan at 3.9% compounded monthly. Payments of $2056 are required at the end of every month. Construct a complete amortization schedule in MS Excel showing the details of all payments and the total.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
73
Rebecca bought a house in Oshawa and took a $259 000 mortgage amortized by monthly payments over 25 years that is renewable after 5 years. If interest is 4.4% compounded semi-annually, what is the outstanding balance at the end of the five year term?
If the mortgage is renewed for a further 5 year term at 3.7% compounded semi-annually, what is the balance after the second 5 year term?
If the mortgage is renewed for a further 5 year term at 3.7% compounded semi-annually, what is the balance after the second 5 year term?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
74
Big Printing Inc. is repaying a loan of $37 300.00 by making payments of $2300.00 at the end of every three months. If interest is 3.5% compounded monthly, construct an amortization schedule showing the total paid and the total cost of the loan. What is the total interest paid and cost of the loan?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
75
John makes a monthly mortgage payment of $1940 at the end of every month. On October 31, his loan balance was $145 000 after making a payment of $1940. His financial institute allows him to make one additional payment equal to or less than his monthly payment, once a month. Taking advantage of that, John made a payment of $1500 on November 15 and $1900 on December 20. What is his year-end balance after making monthly payment on December 31? The effective monthly fixed rate is 0.306%.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
76
Samuel paid $850 000.00 for a new house. He paid $140 000.00 down and financed the balance by making equal payments at the end of every month for 25 years. Interest is 5.1% compounded monthly. What is the total cost of the building for Samuel?
A)$1 397 618
B)$1 412 058
C)$1 400 254
D)$1 404 198
E)$1 257 618
A)$1 397 618
B)$1 412 058
C)$1 400 254
D)$1 404 198
E)$1 257 618

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
77
The Taylors agreed to monthly payments rounded up to the nearest $100.00 on a mortgage of $136 000.00 amortized over 15 years. Interest for the first five years was 8.5% compounded semi-annually. After 30 months, as permitted by the mortgage agreement, the Taylors increased the rounded monthly payment by 10%.
a)Determine the mortgage balance at the end of the five-year term.
b)If the interest rate remains unchanged over the remaining term, how many more of the increased payments will amortize the mortgage balance?
c)How much did the Taylors save by exercising the increase-in-payment option?
a)Determine the mortgage balance at the end of the five-year term.
b)If the interest rate remains unchanged over the remaining term, how many more of the increased payments will amortize the mortgage balance?
c)How much did the Taylors save by exercising the increase-in-payment option?

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
78
Honda is selling a 2014 Accord Coupe Ex M for $30 056.90 including freight, PDI and all applicable fees. The lease payment of $382 is due at the beginning of each month. If the interest rate compounded annually is 3.99% and the residual value is $13 200, determine the size of the final lease payment.
A)$240.51
B)$285.95
C)$150.28
D)$214.13
E)$5.92
A)$240.51
B)$285.95
C)$150.28
D)$214.13
E)$5.92

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
79
Peter worked for GM for 31 years. On his retirement, he opted a pension buy-out and received $1 467 921. He invested his money in an annuity that provided for payments of $9000 at the end of every month. If interest is 4.4% compounded monthly, determine the size of the final payment.

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck
80
Kirk had accumulated $975 000 in his RRSP at the age of 55. He converted the RRSP into an RRIF at that time and started withdrawing $5000 at the beginning of each month. If interest is 4.5% compounded monthly, what is the size of his final withdrawal?
A)$1739.27
B)$1409.28
C)$4947.31
D)$412.07
E)$33.82
A)$1739.27
B)$1409.28
C)$4947.31
D)$412.07
E)$33.82

Unlock Deck
Unlock for access to all 132 flashcards in this deck.
Unlock Deck
k this deck



