Deck 8: Sampling Variability and Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/35
Play
Full screen (f)
Deck 8: Sampling Variability and Sampling Distributions
1
For which of the following combinations of sample size and population proportion would the standard deviation of 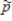 be smallest?
be smallest?
A)n = 40 and p = 0.3
B)n = 60 and p = 0.4
C)n = 100 and p = 0.5
D)n = 200 and p = 0.6
E)n = 300 and p = 0.7
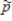 be smallest?
be smallest? A)n = 40 and p = 0.3
B)n = 60 and p = 0.4
C)n = 100 and p = 0.5
D)n = 200 and p = 0.6
E)n = 300 and p = 0.7
n = 300 and p = 0.7
2
The closer p is to 0 or 1, the larger n must be in order for the distribution of 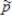 to be approximately normal.
to be approximately normal.
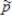 to be approximately normal.
to be approximately normal.True
3
What is a sampling distribution of a statistic?
The distribution of the possible values of a statistic is called its sampling distribution.
Note: Generally if the student communicates the idea that the sampling distribution associates different values of the statistic with their probabilities, he or she should get credit.
Note: Generally if the student communicates the idea that the sampling distribution associates different values of the statistic with their probabilities, he or she should get credit.
4
The principal at John F. Kennedy High School has been asked to provide the average number of classes taken by the students at KHS. Since the computer system is down, she takes her alphabetized list of students, randomly selects 50 students, determines the number of classes each of the 50 selected students is taking, and calculates  = 5.4. She then reports to the PTA "Since I took a large random sample, the population mean number of classes taken by the students at KHS is 5.4." Write a short paragraph to send to her that explains why her statement is not correct.
= 5.4. She then reports to the PTA "Since I took a large random sample, the population mean number of classes taken by the students at KHS is 5.4." Write a short paragraph to send to her that explains why her statement is not correct.
 = 5.4. She then reports to the PTA "Since I took a large random sample, the population mean number of classes taken by the students at KHS is 5.4." Write a short paragraph to send to her that explains why her statement is not correct.
= 5.4. She then reports to the PTA "Since I took a large random sample, the population mean number of classes taken by the students at KHS is 5.4." Write a short paragraph to send to her that explains why her statement is not correct.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose that a particular candidate for public office is favored by 43% of all registered voters in the district A polling organization will take a random sample of 50 of these voters and will use 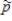 , the sample proportion, to estimate p.
, the sample proportion, to estimate p.
Determine the standard deviation of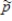 .
.
A)0.005
B)0.035
C)0.100
D)0.043
E)0.070
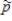 , the sample proportion, to estimate p.
, the sample proportion, to estimate p. Determine the standard deviation of
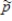 .
.
A)0.005
B)0.035
C)0.100
D)0.043
E)0.070

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following statements is a population proportion?
A)A state census reports that 54% of the state's citizens owns at least one dog..
B)Out of 50 randomly-selected individuals, 19 indicated that they snore during sleep.
C)The mean lifetime of all cell phone batteries is 11.3 hours.
D)For a randomly-selected group of 20 computers running the Ubuntu operating system, the mean boot time was 28 seconds.
E)None of these
A)A state census reports that 54% of the state's citizens owns at least one dog..
B)Out of 50 randomly-selected individuals, 19 indicated that they snore during sleep.
C)The mean lifetime of all cell phone batteries is 11.3 hours.
D)For a randomly-selected group of 20 computers running the Ubuntu operating system, the mean boot time was 28 seconds.
E)None of these

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
7
A sampling distribution of 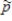 can be regarded as approximately normal when what conditions are met?
can be regarded as approximately normal when what conditions are met?
A)n ≥ 30
B)n ≥ 10
C)np ≥ 5 and n(1 - p) ≥ 5
D)n ≥ 5
E)np ≥ 10 and n(1 - p) ≥ 10
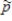 can be regarded as approximately normal when what conditions are met?
can be regarded as approximately normal when what conditions are met? A)n ≥ 30
B)n ≥ 10
C)np ≥ 5 and n(1 - p) ≥ 5
D)n ≥ 5
E)np ≥ 10 and n(1 - p) ≥ 10

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
8
The distribution of 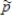 will always have the same shape as the distribution of the population being sampled.
will always have the same shape as the distribution of the population being sampled.
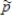 will always have the same shape as the distribution of the population being sampled.
will always have the same shape as the distribution of the population being sampled.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
9
A random sample is to be selected from a population that has a proportion of successes p = 0.50. Determine the mean and standard deviation of the sampling distribution of 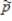 for the sample size n = 100.
for the sample size n = 100.
A)mean: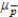 = 0.50; standard deviation:
= 0.50; standard deviation: 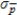 = 0.05
= 0.05
B)mean: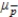 = 0.50; standard deviation:
= 0.50; standard deviation: 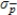 = 0.075
= 0.075
C)mean: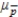 = 0.50; standard deviation:
= 0.50; standard deviation: 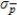 = 0.041
= 0.041
D)mean: = 0.85; standard deviation:
= 0.85; standard deviation: 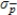 = 0.48
= 0.48
E)mean: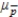 = 0.85; standard deviation:
= 0.85; standard deviation: 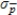 = 0.048
= 0.048
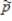 for the sample size n = 100.
for the sample size n = 100. A)mean:
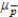 = 0.50; standard deviation:
= 0.50; standard deviation: 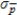 = 0.05
= 0.05B)mean:
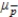 = 0.50; standard deviation:
= 0.50; standard deviation: 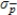 = 0.075
= 0.075C)mean:
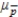 = 0.50; standard deviation:
= 0.50; standard deviation: 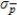 = 0.041
= 0.041D)mean:
 = 0.85; standard deviation:
= 0.85; standard deviation: 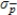 = 0.48
= 0.48E)mean:
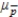 = 0.85; standard deviation:
= 0.85; standard deviation: 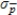 = 0.048
= 0.048
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
10
In a random sample of 79 students at a university, 7 had the flu.
Suppose you are interested in learning about the value of p, the proportion of all students at this university who have the flu. This proportion can be estimated using the sample proportion, . What is the value of
. What is the value of 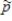 for this sample?
for this sample?
A)0.097
B)0.250
C)0.089
D)0.081
E)0.700
Suppose you are interested in learning about the value of p, the proportion of all students at this university who have the flu. This proportion can be estimated using the sample proportion,
 . What is the value of
. What is the value of 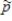 for this sample?
for this sample?
A)0.097
B)0.250
C)0.089
D)0.081
E)0.700

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
11
For n sufficiently large, the distribution of 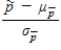 is approximately a standard normal distribution.
is approximately a standard normal distribution.
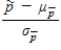 is approximately a standard normal distribution.
is approximately a standard normal distribution.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
12
The sampling distribution of 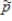 tends to be more spread out for larger sample sizes than for smaller sample sizes.
tends to be more spread out for larger sample sizes than for smaller sample sizes.
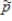 tends to be more spread out for larger sample sizes than for smaller sample sizes.
tends to be more spread out for larger sample sizes than for smaller sample sizes.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
13
If p = 0.90, a sample size of n = 10 is large enough for the sampling distribution to be well approximated by a normal distribution.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
14
The standard deviation of the distribution of 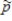 decreases as n increases.
decreases as n increases.
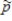 decreases as n increases.
decreases as n increases.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
15
The mean of the sampling distribution of 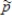 is p no matter how large n is.
is p no matter how large n is.
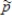 is p no matter how large n is.
is p no matter how large n is.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
16
Some colleges now allow students to rent textbooks for a semester. Suppose that 73% of all students enrolled at a particular college would rent textbooks if that option were available to them. If the campus bookstore uses a random sample of size 40 to estimate the proportion of students at the college who would rent textbooks, then what is the standard deviation of the sampling distribution of 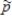 ?
?
A)0.079
B)0.177
C)0.070
D)0.031
E)0.197
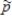 ?
? A)0.079
B)0.177
C)0.070
D)0.031
E)0.197

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
17
A statistic is a characteristic of the population.

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose that 8% of the customers of a cable television company watch the Jewelry Network channel at least once a week. The cable company does not know the actual proportion of all customers who watch the channel at least once a week and is trying to decide whether to replace this channel with a new local station. The company plans to take a random sample of 150 customers and to use 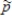 as an estimate of the population proportion.
as an estimate of the population proportion.
Determine the standard deviation of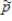 .
.
A)0.022
B)0.006
C)2.400
D)0.070
E)0.041
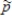 as an estimate of the population proportion.
as an estimate of the population proportion. Determine the standard deviation of
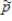 .
.
A)0.022
B)0.006
C)2.400
D)0.070
E)0.041

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
19
As n grows larger, the mean of the sampling distribution of 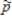 gets closer to μ.
gets closer to μ.
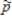 gets closer to μ.
gets closer to μ.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following symbols is used to indicate a population proportion?
A)p
B)
C)μ
D)σ
E)
A)p
B)

C)μ
D)σ
E)


Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
21
One method for estimating abundance of animals is known as line-intercept sampling. The theory of this method, when applied to Alaskan wolverines, predicts that π = 0.453 of attempts to locate wolverine tracks should be successful. Suppose that biologists will make 100 attempts to locate wolverine tracks in random locations in Alaska.
a)Show that this sample size is large enough to justify using the normal approximation to the sampling distribution of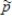 .
.
b)What is the mean of the sampling distribution of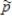 ?
?
c)What is the standard deviation of the sampling distribution of ?
?
a)Show that this sample size is large enough to justify using the normal approximation to the sampling distribution of
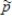 .
.b)What is the mean of the sampling distribution of
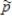 ?
?c)What is the standard deviation of the sampling distribution of
 ?
?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
22
Consider sampling from a population whose proportion of successes is p = 0.5. As the sample size, n, increases, some characteristics of the sampling distribution of 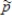 change. Which of the following characteristics will change as n increases, and what is the nature of the change?
change. Which of the following characteristics will change as n increases, and what is the nature of the change?
a)The mean of the sampling distribution of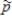 b)The standard deviation of the sampling distribution of
b)The standard deviation of the sampling distribution of  c)The shape of the sampling distribution of
c)The shape of the sampling distribution of 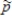
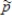 change. Which of the following characteristics will change as n increases, and what is the nature of the change?
change. Which of the following characteristics will change as n increases, and what is the nature of the change?a)The mean of the sampling distribution of
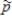 b)The standard deviation of the sampling distribution of
b)The standard deviation of the sampling distribution of  c)The shape of the sampling distribution of
c)The shape of the sampling distribution of 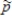

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
23
Determine the mean and standard deviation of the sampling distribution of  when n = 100 and p = 0.65.
when n = 100 and p = 0.65.
 when n = 100 and p = 0.65.
when n = 100 and p = 0.65.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the following "population": {2, 2, 4, 5}. Suppose that a random sample of size n = 2 is to be selected without replacement from this population. There are 6 possible samples (since the order of selection does not matter). Compute the sample mean for each of these samples and use that information to construct the sampling distribution of  . (Display it in table form.)
. (Display it in table form.)
 . (Display it in table form.)
. (Display it in table form.)
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
25
The first large-scale study of the human sex ratio involved over 6,000 families each having 12 children. (This was done in 19th Century Germany--large families were more common then and there.) 52% of the children they observed were boys. Suppose that 21st Century researchers wish to replicate this observational study. In order to see if this proportion of boys might have changed in the intervening years, suppose the researchers track down 50 families with 12 children. From these 600 children, a random sample of 50 children is taken. 30 of the 50 children were boys ( 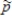 = 0.6.)a)Show that it is reasonable to approximate the sampling distribution of
= 0.6.)a)Show that it is reasonable to approximate the sampling distribution of 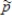 using a normal distribution.
using a normal distribution.
b)If the modern true population proportion of newborn boys is p = 0.52, what is the probability of observing a sample proportion of at least = 0.6?
= 0.6?
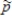 = 0.6.)a)Show that it is reasonable to approximate the sampling distribution of
= 0.6.)a)Show that it is reasonable to approximate the sampling distribution of 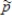 using a normal distribution.
using a normal distribution.b)If the modern true population proportion of newborn boys is p = 0.52, what is the probability of observing a sample proportion of at least
 = 0.6?
= 0.6?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
26
Consider sampling from a population whose proportion of successes is p = 0.1. As the sample size, n, increases, some characteristics of the sampling distribution of 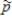 change. Which of the following characteristics will change as n increases, and what is the nature of the change?
change. Which of the following characteristics will change as n increases, and what is the nature of the change?
a)The mean of the sampling distribution of b)The standard deviation of the sampling distribution of
b)The standard deviation of the sampling distribution of 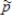 c)The shape of the sampling distribution of
c)The shape of the sampling distribution of 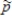
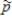 change. Which of the following characteristics will change as n increases, and what is the nature of the change?
change. Which of the following characteristics will change as n increases, and what is the nature of the change?a)The mean of the sampling distribution of
 b)The standard deviation of the sampling distribution of
b)The standard deviation of the sampling distribution of 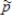 c)The shape of the sampling distribution of
c)The shape of the sampling distribution of 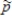

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
27
When the sample size is "large enough," the statistic p has an approximately normal sampling distribution. How does one determine if a sample size is large enough?

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
28
One method for estimating the availability of office space in large cities is to conduct a random sample of offices, and calculate the proportion of offices currently being used. Suppose that real estate agents believe that p = 0.70 of all offices are currently occupied, and decide to take a sample to assess their belief. They are considering a sample size of n = 40.
a)Show that this sample size is large enough to justify using the normal approximation to the sampling distribution of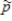 .
.
b)What is the mean of the sampling distribution of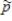 if the real estate agents are correct?
if the real estate agents are correct?
c)What is the standard deviation of the sampling distribution of if the real estate agents are correct?
if the real estate agents are correct?
d)If the real estate agents are correct, what is the probability that a sample proportion,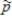 , would differ from p = 0.70 by as much as 0.05?
, would differ from p = 0.70 by as much as 0.05?
a)Show that this sample size is large enough to justify using the normal approximation to the sampling distribution of
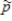 .
.b)What is the mean of the sampling distribution of
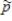 if the real estate agents are correct?
if the real estate agents are correct?c)What is the standard deviation of the sampling distribution of
 if the real estate agents are correct?
if the real estate agents are correct?d)If the real estate agents are correct, what is the probability that a sample proportion,
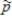 , would differ from p = 0.70 by as much as 0.05?
, would differ from p = 0.70 by as much as 0.05?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the following "population": {1, 1, 3, 4}. Suppose that a random sample of size n = 2 is to be selected without replacement from this population. There are 6 possible samples (since the order of selection does not matter). Compute the sample mean for each of these samples and use that information to construct the sampling distribution of  . (Display it in table form.)
. (Display it in table form.)
 . (Display it in table form.)
. (Display it in table form.)
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
30
Consider sampling from a skewed population. As the sample size, n, increases, some characteristics of the sampling distribution of 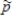 change. Does an increasing sample size cause changes in the characteristics of the sampling distribution shown below? If so, specifically how does the sampling distribution change?
change. Does an increasing sample size cause changes in the characteristics of the sampling distribution shown below? If so, specifically how does the sampling distribution change?
a)The mean of the sampling distribution of b)The standard deviation of the sampling distribution of
b)The standard deviation of the sampling distribution of 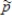 c)The shape of the sampling distribution of
c)The shape of the sampling distribution of 
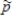 change. Does an increasing sample size cause changes in the characteristics of the sampling distribution shown below? If so, specifically how does the sampling distribution change?
change. Does an increasing sample size cause changes in the characteristics of the sampling distribution shown below? If so, specifically how does the sampling distribution change?a)The mean of the sampling distribution of
 b)The standard deviation of the sampling distribution of
b)The standard deviation of the sampling distribution of 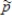 c)The shape of the sampling distribution of
c)The shape of the sampling distribution of 

Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
31
One method for estimating abundance of animals is known as line-intercept sampling. The theory of this method, when applied to Alaskan wolverines, predicts that p = 0.453 of attempts to locate wolverine tracks should be successful. Suppose that biologists will make 100 attempts to locate wolverine tracks in random locations in Alaska.
a)Show that this sample size is large enough to justify using the normal approximation to the sampling distribution of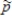 .
.
b)What is the mean of the sampling distribution of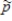 ?
?
c)What is the standard deviation of the sampling distribution of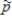 ?
?
d)What is the probability that a sample proportion, , would differ from p = 0.453 by as much as 0.05?
, would differ from p = 0.453 by as much as 0.05?
a)Show that this sample size is large enough to justify using the normal approximation to the sampling distribution of
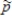 .
.b)What is the mean of the sampling distribution of
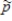 ?
?c)What is the standard deviation of the sampling distribution of
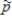 ?
?d)What is the probability that a sample proportion,
 , would differ from p = 0.453 by as much as 0.05?
, would differ from p = 0.453 by as much as 0.05?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
32
Some biologists believe the evolution of handedness is linked to complex behaviors such as tool-use. Under this theory, handedness would be genetically passed on from parents to children. That is, left-handed parents would be more likely to have left-handed children than right-handed parents. An alternate theory asserts that handedness should be random, with left- and right-handedness equally likely. In a recent study using a simple random sample of n = 76 right-handed parents, 50 of the children born were right-handed. ( 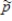 = 0.658.) Suppose handedness is a random occurrence with either hand equally likely to be dominant, implying that the probability of a right-handed offspring is p = 0.50.
= 0.658.) Suppose handedness is a random occurrence with either hand equally likely to be dominant, implying that the probability of a right-handed offspring is p = 0.50.
a)Show that it is reasonable to approximate the sampling distribution of p using a normal distribution.
b)Assuming left- and right-handed children are equally likely from right-handed parents, what is the probability of observing a sample proportion of at least = 0.658?
= 0.658?
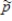 = 0.658.) Suppose handedness is a random occurrence with either hand equally likely to be dominant, implying that the probability of a right-handed offspring is p = 0.50.
= 0.658.) Suppose handedness is a random occurrence with either hand equally likely to be dominant, implying that the probability of a right-handed offspring is p = 0.50.a)Show that it is reasonable to approximate the sampling distribution of p using a normal distribution.
b)Assuming left- and right-handed children are equally likely from right-handed parents, what is the probability of observing a sample proportion of at least
 = 0.658?
= 0.658?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose that the actual proportion of people at a particular company who use their bicycles to travel to job is 0.35. In a study of bicycle parking places needs, administration would like to estimate this proportion. They plan to take a random sample of 50 employees and use the sample proportion who use bicycles, 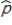 , as an estimate of the population proportion. Estimate the standard deviation of the sample distribution. Suppose that another sample of different size has been selected, and the standard deviation of this new sample is
, as an estimate of the population proportion. Estimate the standard deviation of the sample distribution. Suppose that another sample of different size has been selected, and the standard deviation of this new sample is 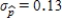 . Would you expect more or less sample-to-sample variability in the sample proportions than for when
. Would you expect more or less sample-to-sample variability in the sample proportions than for when 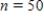 ? Is the sample size that resulted in
? Is the sample size that resulted in 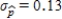 larger or smaller than 50?
larger or smaller than 50?
A)The standard deviation for the initial sample of the size is
is  .Since the standard deviation
.Since the standard deviation 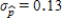 is greater than
is greater than 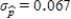 , sample-to-sample variability is less and the new sample size is smaller.
, sample-to-sample variability is less and the new sample size is smaller.
B)The standard deviation for the initial sample of the size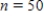 is
is 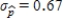 .Since the standard deviation
.Since the standard deviation 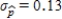 is less than
is less than 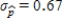 , sample-to-sample variability is more and the new sample size is larger.
, sample-to-sample variability is more and the new sample size is larger.
C)The standard deviation for the initial sample of the size is
is 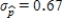 .Since the standard deviation
.Since the standard deviation 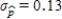 is greater than
is greater than 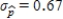 , sample-to-sample variability is more and the new sample size is smaller.
, sample-to-sample variability is more and the new sample size is smaller.
D)The standard deviation for the initial sample of the size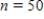 is
is 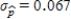 .Since the standard deviation
.Since the standard deviation 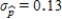 is greater than
is greater than 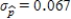 , sample-to-sample variability is more and the new sample size is smaller.
, sample-to-sample variability is more and the new sample size is smaller.
E)The standard deviation for the initial sample of the size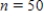 is
is 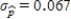 .Since the standard deviation
.Since the standard deviation  is greater than
is greater than 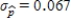 , sample-to-sample variability is less and the new sample size is larger.
, sample-to-sample variability is less and the new sample size is larger.
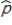 , as an estimate of the population proportion. Estimate the standard deviation of the sample distribution. Suppose that another sample of different size has been selected, and the standard deviation of this new sample is
, as an estimate of the population proportion. Estimate the standard deviation of the sample distribution. Suppose that another sample of different size has been selected, and the standard deviation of this new sample is 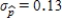 . Would you expect more or less sample-to-sample variability in the sample proportions than for when
. Would you expect more or less sample-to-sample variability in the sample proportions than for when 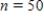 ? Is the sample size that resulted in
? Is the sample size that resulted in 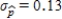 larger or smaller than 50?
larger or smaller than 50?A)The standard deviation for the initial sample of the size
 is
is  .Since the standard deviation
.Since the standard deviation 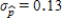 is greater than
is greater than 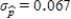 , sample-to-sample variability is less and the new sample size is smaller.
, sample-to-sample variability is less and the new sample size is smaller.B)The standard deviation for the initial sample of the size
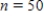 is
is 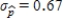 .Since the standard deviation
.Since the standard deviation 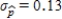 is less than
is less than 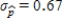 , sample-to-sample variability is more and the new sample size is larger.
, sample-to-sample variability is more and the new sample size is larger.C)The standard deviation for the initial sample of the size
 is
is 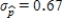 .Since the standard deviation
.Since the standard deviation 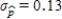 is greater than
is greater than 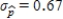 , sample-to-sample variability is more and the new sample size is smaller.
, sample-to-sample variability is more and the new sample size is smaller.D)The standard deviation for the initial sample of the size
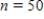 is
is 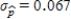 .Since the standard deviation
.Since the standard deviation 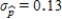 is greater than
is greater than 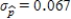 , sample-to-sample variability is more and the new sample size is smaller.
, sample-to-sample variability is more and the new sample size is smaller.E)The standard deviation for the initial sample of the size
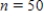 is
is 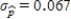 .Since the standard deviation
.Since the standard deviation  is greater than
is greater than 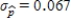 , sample-to-sample variability is less and the new sample size is larger.
, sample-to-sample variability is less and the new sample size is larger.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
34
How are the quantities, p and 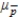 , related?
, related?
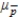 , related?
, related?
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck
35
The principal at Thomas Jefferson High School has been asked to estimate the proportion of students at KHS who drive to school and use the school parking lot. He takes a random sample of size n = 32 students and calculates a sample proportion, 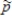 = 0.8. "Now," he exclaims, "since my sample size is greater than 30, the sampling distribution of the sample proportion is approximately normal." Write a short paragraph that explains why his statement is not correct.
= 0.8. "Now," he exclaims, "since my sample size is greater than 30, the sampling distribution of the sample proportion is approximately normal." Write a short paragraph that explains why his statement is not correct.
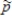 = 0.8. "Now," he exclaims, "since my sample size is greater than 30, the sampling distribution of the sample proportion is approximately normal." Write a short paragraph that explains why his statement is not correct.
= 0.8. "Now," he exclaims, "since my sample size is greater than 30, the sampling distribution of the sample proportion is approximately normal." Write a short paragraph that explains why his statement is not correct.
Unlock Deck
Unlock for access to all 35 flashcards in this deck.
Unlock Deck
k this deck



