Deck 9: Inferences From Two Samples
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/58
Play
Full screen (f)
Deck 9: Inferences From Two Samples
1
Find Consider the set of differences between two dependent sets: 84,85,83,63,61,100,98 . Round to the nearest tenth.
A) 15.3
B) 16.2
C) 15.7
D) 13.1
A) 15.3
B) 16.2
C) 15.7
D) 13.1
15.3
2
When performing a hypothesis test for the ratio of two population variances, the upper critical F value is denoted 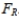 The lower critical F value,
The lower critical F value, 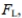 can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5.
can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5. 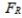 can be denoted
can be denoted 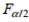 and
and 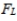 can be denoted
can be denoted 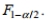
Find the critical values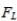 and
and 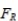 for a two-tailed hypothesis test based on the following values:
for a two-tailed hypothesis test based on the following values: 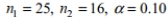
A) 0.7351,2.2378
B) 0.5327,2.2878
C) 0.4745,2.2878
D) 0.4745,2.4371
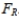 The lower critical F value,
The lower critical F value, 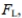 can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5.
can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5. 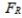 can be denoted
can be denoted 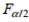 and
and 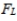 can be denoted
can be denoted 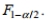
Find the critical values
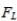 and
and 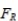 for a two-tailed hypothesis test based on the following values:
for a two-tailed hypothesis test based on the following values: 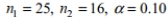
A) 0.7351,2.2378
B) 0.5327,2.2878
C) 0.4745,2.2878
D) 0.4745,2.4371
0.4745,2.2878
3
Assume that you plan to use a significance level of 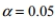
to test the claim that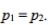 Use the given sample sizes and numbers of successes to find the pooled estimate
Use the given sample sizes and numbers of successes to find the pooled estimate 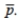 Round your answer to the nearest thousandth.
Round your answer to the nearest thousandth.
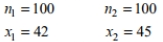
A) 0.479
B) 0.435
C) 0.305
D) 0.392
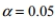
to test the claim that
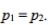 Use the given sample sizes and numbers of successes to find the pooled estimate
Use the given sample sizes and numbers of successes to find the pooled estimate 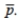 Round your answer to the nearest thousandth.
Round your answer to the nearest thousandth.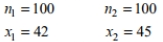
A) 0.479
B) 0.435
C) 0.305
D) 0.392
0.435
4
Determine whether the samples are independent or dependent. The effectiveness of a headache medicine is tested by measuring the intensity of a headache in patients before and after drug
Treatment. The data consist of before and after intensities for each patient.

A)Independent samples
B)Dependent samples
Treatment. The data consist of before and after intensities for each patient.

A)Independent samples
B)Dependent samples

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
5
Assume that two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal.
Which distribution is used to test the claim that women have a higher mean resting heart rate
Than men?
A)Normal
B)t
C)chi-square
D)F
Which distribution is used to test the claim that women have a higher mean resting heart rate
Than men?
A)Normal
B)t
C)chi-square
D)F

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether the following statement regarding the hypothesis test for two population
proportions is true or false:
However small the difference between two population proportions, for sufficiently large
sample sizes, the null hypothesis of equal population proportions is likely to be rejected.
proportions is true or false:
However small the difference between two population proportions, for sufficiently large
sample sizes, the null hypothesis of equal population proportions is likely to be rejected.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
7
Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from normally distributed populations. Do not assume that the population standard deviations are equal. Independent samples from two different populations yield the following data.
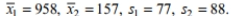
The sample size is 478 for both samples. Find the 85 % confidence interval for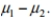
A)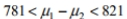
B)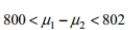
C)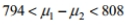
D)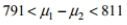
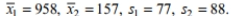
The sample size is 478 for both samples. Find the 85 % confidence interval for
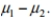
A)
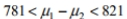
B)
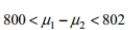
C)
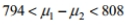
D)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
8
Find sd. The differences between two sets of dependent data are 0.4, 0.24, 0.22, 0.26, 0.34._ Round to the nearest hundredth.
A)0.08
B)0.12
C)0.04
D)0.24
A)0.08
B)0.12
C)0.04
D)0.24

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
9
A paint manufacturer made a modification to a paint to speed up its drying time. Independent_ simple random samples of 11 cans of type A (the original paint)and 9 cans of type B (the
Modified paint)were selected and applied to similar surfaces. The drying times, in hours, were
Recorded. The summary statistics are as follows.
Modified paint)were selected and applied to similar surfaces. The drying times, in hours, were
Recorded. The summary statistics are as follows.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
10
Construct the indicated confidence interval for the difference between the two population_ means. Assume that the two samples are independent simple random samples selected from
Normally distributed populations. Do not assume that the population standard deviations are
Equal. A paint manufacturer wished to compare the drying times of two different types of
Paint. Independent simple random samples of 11 cans of type A and 9 cans of type B were
Selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.
Construct a confidence interval for , the difference between the mean drying time for paint of type and the mean drying time for paint of type .
A)
B)
C)
D)
Normally distributed populations. Do not assume that the population standard deviations are
Equal. A paint manufacturer wished to compare the drying times of two different types of
Paint. Independent simple random samples of 11 cans of type A and 9 cans of type B were
Selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.
Construct a confidence interval for , the difference between the mean drying time for paint of type and the mean drying time for paint of type .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
11
Assume that you plan to use a significance level of 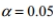 to test the claim that
to test the claim that 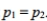 Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.

A) 0.7794
B) 0.3897
C) 0.6103
D) 0.2206
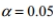 to test the claim that
to test the claim that 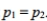 Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
A) 0.7794
B) 0.3897
C) 0.6103
D) 0.2206

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
12
The two data sets are dependent. Find 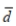 to the nearest tenth.
to the nearest tenth.
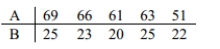
A) 50.7
B) 23.4
C) 48.8
D) 39.0
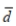 to the nearest tenth.
to the nearest tenth.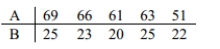
A) 50.7
B) 23.4
C) 48.8
D) 39.0

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
13
When testing the claim that 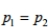 , a test statistic of z=2.04 is obtained. Find the P -value obtained from this test statistic.
, a test statistic of z=2.04 is obtained. Find the P -value obtained from this test statistic.
A) 0.9586
B) 0.0207
C) 0.9793
D) 0.0414
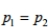 , a test statistic of z=2.04 is obtained. Find the P -value obtained from this test statistic.
, a test statistic of z=2.04 is obtained. Find the P -value obtained from this test statistic.A) 0.9586
B) 0.0207
C) 0.9793
D) 0.0414

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
14
Determine the decision criterion for rejecting the null hypothesis in the given hypothesis test; i.e., describe the values of the test statistic that would result in rejection of the null hypothesis. We wish to compare the means of two populations using paired observations. Suppose that 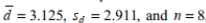 and that you wish to test the following hypothesis at the
and that you wish to test the following hypothesis at the
10 % level of significance:
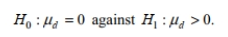
What decision rule would you use?
A) Reject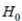 if the test statistic is less than 1.415 .
if the test statistic is less than 1.415 .
B) Reject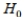 if the test statistic is greater than -1.145 .
if the test statistic is greater than -1.145 .
C) Reject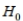 if the test statistic is greater than -1.145 or less than 1.415 .
if the test statistic is greater than -1.145 or less than 1.415 .
D) Reject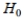 if the test statistic is greater than 1.415 .
if the test statistic is greater than 1.415 .
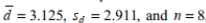 and that you wish to test the following hypothesis at the
and that you wish to test the following hypothesis at the10 % level of significance:
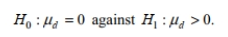
What decision rule would you use?
A) Reject
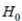 if the test statistic is less than 1.415 .
if the test statistic is less than 1.415 . B) Reject
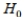 if the test statistic is greater than -1.145 .
if the test statistic is greater than -1.145 .C) Reject
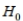 if the test statistic is greater than -1.145 or less than 1.415 .
if the test statistic is greater than -1.145 or less than 1.415 .D) Reject
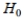 if the test statistic is greater than 1.415 .
if the test statistic is greater than 1.415 .
Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
15
Which distribution is used to test the claim that the standard deviation of the ages (in years)of when girls first learn to ride a bike is equal to the standard deviation of the ages (in years)
When boys first lean to ride a bike?
A)Normal
B)t
C)chi-square
D)F
When boys first lean to ride a bike?
A)Normal
B)t
C)chi-square
D)F

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
16
Determine the decision criterion for rejecting the null hypothesis in the given hypothesis test; i.e., describe the values of the test statistic that would result in rejection of the null hypothesis. Suppose you wish to test the claim that 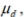 the mean value of the differences d for a population of paired data, is greater than 0 . Given a sample of n=15 and a significance level of
the mean value of the differences d for a population of paired data, is greater than 0 . Given a sample of n=15 and a significance level of 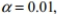 what criterion would be used for rejecting the null hypothesis?
what criterion would be used for rejecting the null hypothesis?
A) Reject null hypothesis if test statistic <2.624 .
B) Reject null hypothesis if test statistic >2.602 .
C) Reject null hypothesis if test statistic >2.624 .
D) Reject null hypothesis if test statistic >2.977 or <-2.977 .
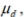 the mean value of the differences d for a population of paired data, is greater than 0 . Given a sample of n=15 and a significance level of
the mean value of the differences d for a population of paired data, is greater than 0 . Given a sample of n=15 and a significance level of 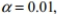 what criterion would be used for rejecting the null hypothesis?
what criterion would be used for rejecting the null hypothesis?A) Reject null hypothesis if test statistic <2.624 .
B) Reject null hypothesis if test statistic >2.602 .
C) Reject null hypothesis if test statistic >2.624 .
D) Reject null hypothesis if test statistic >2.977 or <-2.977 .

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
17
Assume that the following confidence interval for the difference in the mean length of male (sample 1) and female babies (sample 2) at birth was constructed using independent simple random samples. -0.2 in 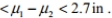
What does the confidence interval suggest about the difference in length between male babies and female babies?
A) Male babies are longer.
B) Female babies are longer.
C) There is no difference in the length between male and female babies.
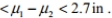
What does the confidence interval suggest about the difference in length between male babies and female babies?
A) Male babies are longer.
B) Female babies are longer.
C) There is no difference in the length between male and female babies.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
18
If the heights of male college basketball players and female basketball players are used to construct a 95 % confidence interval for the difference between the two population means, the result is 15.35 cm 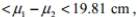
where heights of male players correspond to population 1 and heights of female players correspond to population 2. Express the confidence interval with heights of female basketball players being population 1 and heights of male basketball players being population 2 .
A)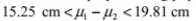
B)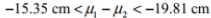
C)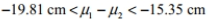
D) This cannot be determined without having the original data values.
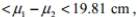
where heights of male players correspond to population 1 and heights of female players correspond to population 2. Express the confidence interval with heights of female basketball players being population 1 and heights of male basketball players being population 2 .
A)
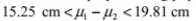
B)
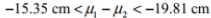
C)
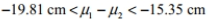
D) This cannot be determined without having the original data values.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
19
Express the alternative hypothesis in symbolic form. of time (in hours)sophomores spent studying for the statistics final exam is more than that of
Freshmen. Assume that the two samples are independent. Let the freshmen be the first
Population and the sophomores be the second population.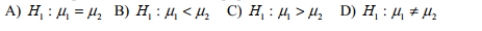
Freshmen. Assume that the two samples are independent. Let the freshmen be the first
Population and the sophomores be the second population.
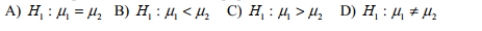

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
20
Assume that you plan to use a significance level of 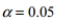 to test the claim that
to test the claim that 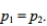 Use the given sample sizes and numbers of successes to find the pooled estimate
Use the given sample sizes and numbers of successes to find the pooled estimate 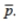 Round your answer to the nearest thousandth.
Round your answer to the nearest thousandth.

A) 0.163
B) 0.452
C) 0.204
D) 0.408
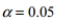 to test the claim that
to test the claim that 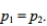 Use the given sample sizes and numbers of successes to find the pooled estimate
Use the given sample sizes and numbers of successes to find the pooled estimate 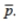 Round your answer to the nearest thousandth.
Round your answer to the nearest thousandth.
A) 0.163
B) 0.452
C) 0.204
D) 0.408

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
21
Assume that you plan to use a significance level of 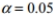 to test the claim that
to test the claim that  Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
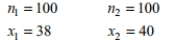
A) 0.1610
B) 0.2130
C) 0.0412
D) 0.7718
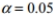 to test the claim that
to test the claim that  Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.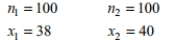
A) 0.1610
B) 0.2130
C) 0.0412
D) 0.7718

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
22
In the context of a hypothesis test for two proportions, which of the following statements about the pooled sample proportion, 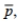 is/are true?
is/are true?
I. It estimates the common value of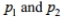 under the assumption of equal proportions.
under the assumption of equal proportions.
II. It is obtained by averaging the two sample proportions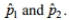
III. It is equal to the proportion of successes in both samples combined.
A) I and II
B) III only
C) I, II, and III
D) I and III
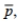 is/are true?
is/are true?I. It estimates the common value of
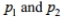 under the assumption of equal proportions.
under the assumption of equal proportions.II. It is obtained by averaging the two sample proportions
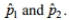
III. It is equal to the proportion of successes in both samples combined.
A) I and II
B) III only
C) I, II, and III
D) I and III

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
23
Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is 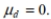
Compute the value of the t test statistics. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.
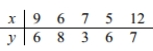
A) t=0.578
B) t=2.890
C) t=1.292
D) t=0.415
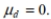
Compute the value of the t test statistics. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.
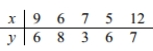
A) t=0.578
B) t=2.890
C) t=1.292
D) t=0.415

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
24
Find the number of successes x suggested by the given statement. A computer manufacturer_ randomly selects 2680 of its computers for quality assurance and finds that 1.98% of these
Computers are found to be defective.
A)56
B)51
C)58
D)53
Computers are found to be defective.
A)56
B)51
C)58
D)53

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
25
A test of abstract reasoning is given to a random sample of students before and after they_ completed a formal logic course. The results are given below. Construct a 95% confidence
Interval for the mean difference between the before and after scores.
A)
B)
C)
D)
Interval for the mean difference between the before and after scores.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
26
Determine whether the samples are dependent or independent. The effectiveness of a_ headache medicine is tested by measuring the intensity of a headache in patients before and
After drug treatment. The data consist of before and after intensities for each patient.
A)Dependent samples
B)Independent samples
After drug treatment. The data consist of before and after intensities for each patient.
A)Dependent samples
B)Independent samples

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
27
When performing a hypothesis test for the ratio of two population variances, the upper critical F value is denoted 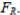 The lower critical F value,
The lower critical F value,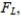 can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5.
can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5. 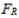 can be denoted
can be denoted 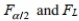
can be denoted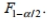
Find the critical values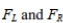
for a two-tailed hypothesis test based on the following values: n1=9, n2 -7 ,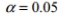
A) 0.2150,5.5996
B) 0.2150,4.8232
C) 0.3931,4.1468
D) 0.2411,4.1468
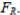 The lower critical F value,
The lower critical F value,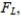 can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5.
can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in Table A-5. 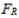 can be denoted
can be denoted 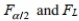
can be denoted
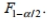
Find the critical values
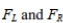
for a two-tailed hypothesis test based on the following values: n1=9, n2 -7 ,
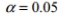
A) 0.2150,5.5996
B) 0.2150,4.8232
C) 0.3931,4.1468
D) 0.2411,4.1468

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
28
Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is 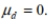 Compute the value of the t test statistic. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.
Compute the value of the t test statistic. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.

A) 9.468
B) 3.156
C) 0.351
D) 1.052
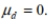 Compute the value of the t test statistic. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.
Compute the value of the t test statistic. Round intermediate calculations to four decimal places as needed and final answers to three decimal places as needed.
A) 9.468
B) 3.156
C) 0.351
D) 1.052

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
29
Assume that the following confidence interval for the difference in the mean time (in minutes) for male students to complete a statistics test (sample 1) and the mean time for female students to complete a statistics test (sample 2) was constructed using independent simple random samples. -0.2 minutes 
What does the confidence interval suggest about the difference in length between male and female test completion times?
A) Male students take longer to complete a statistics test.
B) Female students take longer to complete a statistics test.
C) There is no difference in the length of time for statistics test completion between male and female students.

What does the confidence interval suggest about the difference in length between male and female test completion times?
A) Male students take longer to complete a statistics test.
B) Female students take longer to complete a statistics test.
C) There is no difference in the length of time for statistics test completion between male and female students.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
30
Construct a confidence interval for 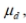 the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct a 90 % confidence interval for the population mean of all differences.
the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct a 90 % confidence interval for the population mean of all differences.
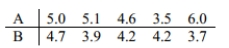
A)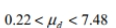
B)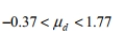
C)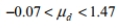
D)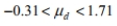
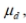 the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct a 90 % confidence interval for the population mean of all differences.
the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. Using the sample paired data below, construct a 90 % confidence interval for the population mean of all differences.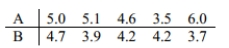
A)
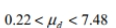
B)
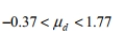
C)
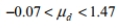
D)
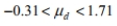

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
31
Assume that two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal.
Which distribution is used to test the claim that mothers spend more time (in minutes)
Driving their kids to activities than fathers do?
A)Normal
B)t
C)chi-square
D)F
Which distribution is used to test the claim that mothers spend more time (in minutes)
Driving their kids to activities than fathers do?
A)Normal
B)t
C)chi-square
D)F

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
32
Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from
Normally distributed populations. Also assume that the population standard deviations are
Equal , so that the standard error of the difference between means is obtained by
Pooling the sample variances. A paint manufacturer wanted to compare the drying times of
Two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours,
Were recorded. The summary statistics are as follows.
Construct a confidence interval for , the difference between the mean drying time for paint type and the mean drying time for paint type .
A)
B)
C)
D)
Normally distributed populations. Also assume that the population standard deviations are
Equal , so that the standard error of the difference between means is obtained by
Pooling the sample variances. A paint manufacturer wanted to compare the drying times of
Two different types of paint. Independent simple random samples of 11 cans of type A and 9
Cans of type B were selected and applied to similar surfaces. The drying times, in hours,
Were recorded. The summary statistics are as follows.
Construct a confidence interval for , the difference between the mean drying time for paint type and the mean drying time for paint type .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
33
Construct a confidence interval for 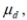 the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. A test of writing ability is given to a random sample of students before and after they completed a formal writing course. The results are given below. Construct a 99 % confidence interval for the mean difference between the before and after scores.
the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. A test of writing ability is given to a random sample of students before and after they completed a formal writing course. The results are given below. Construct a 99 % confidence interval for the mean difference between the before and after scores.
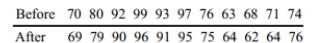
A)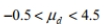
B)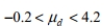
C)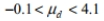
D)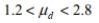
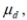 the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. A test of writing ability is given to a random sample of students before and after they completed a formal writing course. The results are given below. Construct a 99 % confidence interval for the mean difference between the before and after scores.
the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed. A test of writing ability is given to a random sample of students before and after they completed a formal writing course. The results are given below. Construct a 99 % confidence interval for the mean difference between the before and after scores.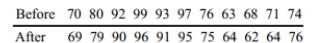
A)
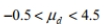
B)
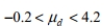
C)
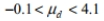
D)
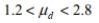

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
34
Determine whether the samples are dependent or independent. The effectiveness of a new_ headache medicine is tested by measuring the amount of time before the headache is cured
For patients who use the medicine and another group of patients who use a placebo drug.
A)Dependent samples
B)Independent samples
For patients who use the medicine and another group of patients who use a placebo drug.
A)Dependent samples
B)Independent samples

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
35
If the lengths of male skis and female skis are used to construct a 95 % confidence interval for the difference between the two population means, the result is
14.32 cm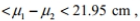
where lengths of male skis correspond to population 1 and lengths of female skis correspond to population 2. Express the confidence interval with the lengths of female skis being population 1 and lengths of male skis being population
A)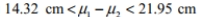
B)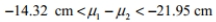
C)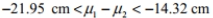
D) This cannot be determined without having the original data values.
14.32 cm
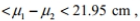
where lengths of male skis correspond to population 1 and lengths of female skis correspond to population 2. Express the confidence interval with the lengths of female skis being population 1 and lengths of male skis being population
A)
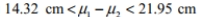
B)
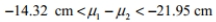
C)
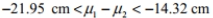
D) This cannot be determined without having the original data values.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
36
Which distribution is used to test the claim that the standard deviation of the lengths (in cm)18)___________ of male babies at birth is equal to the standard deviation of the lengths (in cm)of female
Babies at birth?
A)Normal
B)t
C)chi-square
D)F
Babies at birth?
A)Normal
B)t
C)chi-square
D)F

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
37
Assume that you plan to use a significance level of 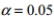 to test the claim that
to test the claim that 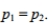 Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
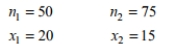
A) 0.1201
B) 0.0032
C) 0.0001
D) 0.0146
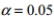 to test the claim that
to test the claim that 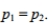 Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.
Use the given sample sizes and numbers of successes to find the P -value for the hypothesis test.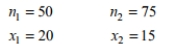
A) 0.1201
B) 0.0032
C) 0.0001
D) 0.0146

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
38
A researcher wishes to compare how students at two different schools perform on a math test._
He randomly selects 40 students from each school and obtains their test scores. He pairs the
first score from school A with the first school from school B, the second score from school A
with the second school from school B and so on. He then performs a hypothesis test for
matched pairs. Is this approach valid? Why or why not? If it is not valid, how should the
researcher have proceeded?
He randomly selects 40 students from each school and obtains their test scores. He pairs the
first score from school A with the first school from school B, the second score from school A
with the second school from school B and so on. He then performs a hypothesis test for
matched pairs. Is this approach valid? Why or why not? If it is not valid, how should the
researcher have proceeded?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
39
Construct the indicated confidence interval for the difference between the two population means. Assume that the two samples are independent simple random samples selected from
Normally distributed populations. Do not assume that the population standard deviations are
Equal. A paint manufacturer wished to compare the drying times of two different types of
Paint .Independent simple random samples of 11 cans of type A and 9 cans of type B were
Selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.
Construct a confidence interval for , the difference between the mean drying time for paint type A and the mean drying time for paint type .
A)
B)
C)
D)
Normally distributed populations. Do not assume that the population standard deviations are
Equal. A paint manufacturer wished to compare the drying times of two different types of
Paint .Independent simple random samples of 11 cans of type A and 9 cans of type B were
Selected and applied to similar surfaces. The drying times, in hours, were recorded. The
Summary statistics are as follows.
Construct a confidence interval for , the difference between the mean drying time for paint type A and the mean drying time for paint type .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
40
Express the alternative hypothesis in symbolic form. An automobile technician claims that the mean amount of time (in hours)per domestic car repair is more than that of foreign cars.
Assume that two samples are independent. Let the domestic car repair times be the first
Population and the foreign car repair times be the second population.
Assume that two samples are independent. Let the domestic car repair times be the first
Population and the foreign car repair times be the second population.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
41
Assume that the two samples are independent simple random samples selected from normally
distributed populations. Do not assume that the population standard deviations are equal. A
researcher wishes to determine whether people can reduce their resting heart rate by following
a particular diet. Construct a 95% confidence interval estimate for the following data. Does
the confidence interval support that the mean resting heart rate for those on the diet is lower
than that of those not on the diet? Explain your reasoning.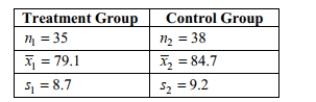
distributed populations. Do not assume that the population standard deviations are equal. A
researcher wishes to determine whether people can reduce their resting heart rate by following
a particular diet. Construct a 95% confidence interval estimate for the following data. Does
the confidence interval support that the mean resting heart rate for those on the diet is lower
than that of those not on the diet? Explain your reasoning.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
42
Assume
marketing survey involves product recognition in New York and California. Of 558 New
Yorkers surveyed, 193 knew the product while 196 out of 614 Californians knew the product.
At the 0.05 significance level, test the claim that the recognition rates are the same in both
states. Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
conclusion about the null hypothesis, and conclusion about the claim in your answer.
marketing survey involves product recognition in New York and California. Of 558 New
Yorkers surveyed, 193 knew the product while 196 out of 614 Californians knew the product.
At the 0.05 significance level, test the claim that the recognition rates are the same in both
states. Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
conclusion about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
43
To test the null hypothesis that the difference between two population proportions is
equal to a nonzero constant c, use the test statistic
equal to a nonzero constant c, use the test statistic


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
44
A Dean of Students conducted a survey to test the claim that women spend more time visiting
the STEM lab than men do. A survey was administered to a simple random sample of 15
female student volunteers and 12 male volunteers that asked, "How many minutes have you
spent in the STEM lab this semester?" The results are shown below.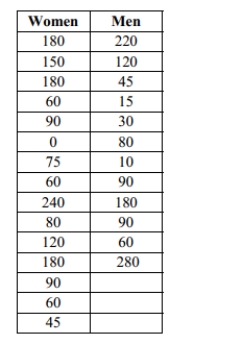 Test the claim at the 1% level of significance. Assume that the number of minutes that
Test the claim at the 1% level of significance. Assume that the number of minutes that
women and men spent in the STEM lab is normally distributed. Do not assume that the
population standard deviations are equal. Include your null and alternative hypotheses, the
test statistic, P-value or critical value(s), conclusion about the null hypothesis, and conclusion
about the claim in your answer.
the STEM lab than men do. A survey was administered to a simple random sample of 15
female student volunteers and 12 male volunteers that asked, "How many minutes have you
spent in the STEM lab this semester?" The results are shown below.
 Test the claim at the 1% level of significance. Assume that the number of minutes that
Test the claim at the 1% level of significance. Assume that the number of minutes thatwomen and men spent in the STEM lab is normally distributed. Do not assume that the
population standard deviations are equal. Include your null and alternative hypotheses, the
test statistic, P-value or critical value(s), conclusion about the null hypothesis, and conclusion
about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
45
Test the given claim about the means of two populations. Assume that two dependent samples
have been randomly selected from normally distributed populations.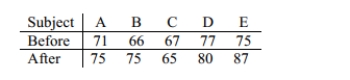 Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math
Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math
scores. Include your null and alternative hypotheses, the test statistic, P-value or critical
value(s), conclusion about the null hypothesis, and conclusion about the claim in your answer.
have been randomly selected from normally distributed populations.
 Using a 0.01 level of significance, test the claim that the tutoring has an effect on the math
Using a 0.01 level of significance, test the claim that the tutoring has an effect on the mathscores. Include your null and alternative hypotheses, the test statistic, P-value or critical
value(s), conclusion about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
46
A researcher wishes to determine whether the blood pressure of vegetarians is, on average,_
lower than the blood pressure of nonvegetarians. Independent simple random samples of 85
vegetarians and 75 nonvegetarians yielded the following sample statistics for systolic blood
pressure: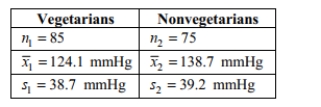 Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of
Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of
vegetarians is lower than the mean systolic blood pressure of nonvegetarians. Include your null
and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the
null hypothesis, and conclusion about the claim in your answer.
lower than the blood pressure of nonvegetarians. Independent simple random samples of 85
vegetarians and 75 nonvegetarians yielded the following sample statistics for systolic blood
pressure:
 Use a significance level of 0.01 to test the claim that the mean systolic blood pressure of
Use a significance level of 0.01 to test the claim that the mean systolic blood pressure ofvegetarians is lower than the mean systolic blood pressure of nonvegetarians. Include your null
and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the
null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
47
Test the indicated claim about the variances or standard deviations of two populations.
Assume that both samples are independent simple random samples from populations having
normal distributions. A random sample of 16 women resulted in blood pressure levels with a
standard deviation of 23 mm Hg. A random sample of 17 men resulted in blood pressure
levels with a standard deviation of 19.2 mm Hg. Use a 0.05 significance level to test the claim
that blood pressure levels for women vary more than blood pressure levels for men. Include
your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion
about the null hypothesis, and conclusion about the claim in your answer.
Assume that both samples are independent simple random samples from populations having
normal distributions. A random sample of 16 women resulted in blood pressure levels with a
standard deviation of 23 mm Hg. A random sample of 17 men resulted in blood pressure
levels with a standard deviation of 19.2 mm Hg. Use a 0.05 significance level to test the claim
that blood pressure levels for women vary more than blood pressure levels for men. Include
your null and alternative hypotheses, the test statistic, P-value or critical value(s), conclusion
about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
48
Brian wants to obtain a confidence interval estimate of 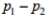 where
where 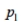 represents the proportion of American women who smoke and
represents the proportion of American women who smoke and 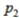 represents the proportion of American men who smoke. He randomly selects 100 married couples. Among the 100 women in the sample are 21 smokers. Among the 100 men are 29 smokers. Are the requirements for obtaining a confidence interval estimate of
represents the proportion of American men who smoke. He randomly selects 100 married couples. Among the 100 women in the sample are 21 smokers. Among the 100 men are 29 smokers. Are the requirements for obtaining a confidence interval estimate of 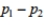 satisfied? If not, which requirement is not satisfied?
satisfied? If not, which requirement is not satisfied?
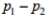 where
where 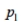 represents the proportion of American women who smoke and
represents the proportion of American women who smoke and 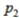 represents the proportion of American men who smoke. He randomly selects 100 married couples. Among the 100 women in the sample are 21 smokers. Among the 100 men are 29 smokers. Are the requirements for obtaining a confidence interval estimate of
represents the proportion of American men who smoke. He randomly selects 100 married couples. Among the 100 women in the sample are 21 smokers. Among the 100 men are 29 smokers. Are the requirements for obtaining a confidence interval estimate of 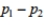 satisfied? If not, which requirement is not satisfied?
satisfied? If not, which requirement is not satisfied?
Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
49
Test the indicated claim about the means of two populations. Assume that the two samples are
independent simple random samples selected from normally distributed populations. Do not
assume that the population standard deviations are equal. A researcher wishes to determine
whether people with high blood pressure can reduce their blood pressure, measured in mm Hg,
by following a particular diet. Use a significance level of 0.01 to test the claim that the treatment
group is from a population with a smaller mean than the control group. Include your null and
alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.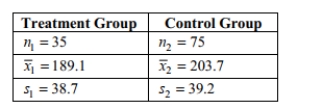
independent simple random samples selected from normally distributed populations. Do not
assume that the population standard deviations are equal. A researcher wishes to determine
whether people with high blood pressure can reduce their blood pressure, measured in mm Hg,
by following a particular diet. Use a significance level of 0.01 to test the claim that the treatment
group is from a population with a smaller mean than the control group. Include your null and
alternative hypotheses, the test statistic, P-value or critical value(s), conclusion about the null
hypothesis, and conclusion about the claim in your answer.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
50
Test the given claim about the means of two populations. Assume that two dependent samples_
have been randomly selected from normally distributed populations. A test of abstract reasoning
is given to a random sample of students before and after they completed a formal logic course.
The results are given below. At the 0.05 significance level, test the claim that the mean score is
not affected by the course. Include your null and alternative hypotheses, the test statistic, P-value
or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your
answer.
have been randomly selected from normally distributed populations. A test of abstract reasoning
is given to a random sample of students before and after they completed a formal logic course.
The results are given below. At the 0.05 significance level, test the claim that the mean score is
not affected by the course. Include your null and alternative hypotheses, the test statistic, P-value
or critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your
answer.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
51
Test the indicated claim about the means of two populations. Assume that the two samples are
independent simple random samples selected from normally distributed populations. Do not
assume that the population standard deviations are equal.
independent simple random samples selected from normally distributed populations. Do not
assume that the population standard deviations are equal.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
52
When testing for a difference between the means of a treatment group and a placebo group, the
computer display below is obtained. Using a 0.05 significance level, is there sufficient evidence
to support the claim that the treatment group (variable 1)comes from a population with a mean
that is less than the mean for the placebo population? Explain.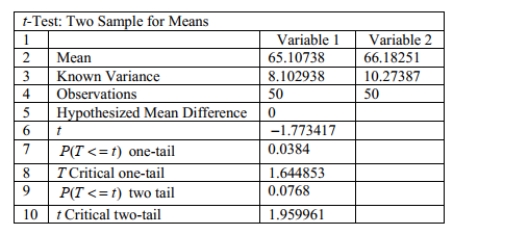
computer display below is obtained. Using a 0.05 significance level, is there sufficient evidence
to support the claim that the treatment group (variable 1)comes from a population with a mean
that is less than the mean for the placebo population? Explain.


Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
53
Identify the test statistic that should be used for testing the following given claims.
a. The mean of the differences between IQ scores of brothers and IQ scores of their sisters is
equal to 0.
b. The proportion of offices with windows is equal to the proportion of offices without
windows.
c. The variation among temperature inside buildings in winter is equal to the variation in the
temperature inside building in summer.
d. The mean age of female math professors is equal to the mean age of male math professors.
a. The mean of the differences between IQ scores of brothers and IQ scores of their sisters is
equal to 0.
b. The proportion of offices with windows is equal to the proportion of offices without
windows.
c. The variation among temperature inside buildings in winter is equal to the variation in the
temperature inside building in summer.
d. The mean age of female math professors is equal to the mean age of male math professors.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
54
Test the given claim about the means of two populations. Assume that two dependent samples_
have been randomly selected from normally distributed populations. A coach uses a new
technique to train gymnasts. 7 gymnasts were randomly selected and their competition scores
were recorded before and after the training. The results are shown below. Using a 0.01 level of significance, test the claim that the training technique is effective in raising
Using a 0.01 level of significance, test the claim that the training technique is effective in raising
the gymnasts' scores. Include your null and alternative hypotheses, the test statistic, P-value or
critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your
answer.
have been randomly selected from normally distributed populations. A coach uses a new
technique to train gymnasts. 7 gymnasts were randomly selected and their competition scores
were recorded before and after the training. The results are shown below.
 Using a 0.01 level of significance, test the claim that the training technique is effective in raising
Using a 0.01 level of significance, test the claim that the training technique is effective in raisingthe gymnasts' scores. Include your null and alternative hypotheses, the test statistic, P-value or
critical value(s), conclusion about the null hypothesis, and conclusion about the claim in your
answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
55
Suppose you wish to test a claim about the mean of the differences from dependent samples or_
to construct a confidence interval estimate of the mean of the differences from dependent
samples. What are the requirements?
to construct a confidence interval estimate of the mean of the differences from dependent
samples. What are the requirements?

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
56
Test the indicated claim about the means of two populations. Assume that the two samples are
independent simple random samples selected from normally distributed populations. Do not
assume that the population standard deviations are equal.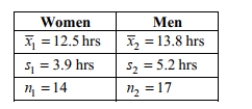 Use a 0.05 significance level to test the claim that the mean amount of time spent watching
Use a 0.05 significance level to test the claim that the mean amount of time spent watching
television by women is smaller than the mean amount of time spent watching television by
men. Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
conclusion about the null hypothesis, and conclusion about the claim in your answer.
independent simple random samples selected from normally distributed populations. Do not
assume that the population standard deviations are equal.
 Use a 0.05 significance level to test the claim that the mean amount of time spent watching
Use a 0.05 significance level to test the claim that the mean amount of time spent watchingtelevision by women is smaller than the mean amount of time spent watching television by
men. Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
conclusion about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
57
In a random sample of 300 women, 45% favored stricter DUI legislation. In a random
sample of 200 men, 25% favored stricter DUI legislation. Construct a 95% confidence
interval for the difference between the population proportions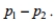 . Assume that the
. Assume that the
samples are independent and that they have been randomly selected.
sample of 200 men, 25% favored stricter DUI legislation. Construct a 95% confidence
interval for the difference between the population proportions
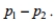 . Assume that the
. Assume that thesamples are independent and that they have been randomly selected.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck
58
A random sample of 10 employees of an engineering company was selected. Each employee
was asked to report the number of sick days he/she claimed on Wednesdays and Fridays of
the previous calendar year. Use this information to test the employer's claim that more
employees call in sick on Fridays than on Wednesdays. Assume that the
Assume that the
differences between Wednesday's and Friday's sick day counts is normally distributed.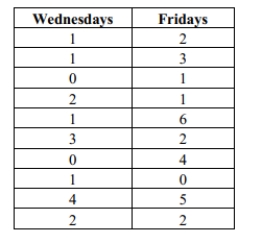 Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
conclusion about the null hypothesis, and conclusion about the claim in your answer.
was asked to report the number of sick days he/she claimed on Wednesdays and Fridays of
the previous calendar year. Use this information to test the employer's claim that more
employees call in sick on Fridays than on Wednesdays.
 Assume that the
Assume that thedifferences between Wednesday's and Friday's sick day counts is normally distributed.
 Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),
Include your null and alternative hypotheses, the test statistic, P-value or critical value(s),conclusion about the null hypothesis, and conclusion about the claim in your answer.

Unlock Deck
Unlock for access to all 58 flashcards in this deck.
Unlock Deck
k this deck



