Deck 3: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/283
Play
Full screen (f)
Deck 3: Probability
1
A bag of colored candies contains 20 red, 25 yellow, and 35 orange candies. An experiment consists of randomly choosing one candy from the bag and recording its color. What is the sample space for this experiment?
A) {red, yellow, orange}
B) {20, 25, 35}
C) {1/4, 5/16, 7/16}
D) {80}
A) {red, yellow, orange}
B) {20, 25, 35}
C) {1/4, 5/16, 7/16}
D) {80}
A
2
A bag of candy was opened and the number of pieces was counted. The results are shown in the table below: Find the probability that a randomly chosen piece of candy is not blue or red.
A) 0.40
B) 0.85
C) 0.15
D) 0.60
A) 0.40
B) 0.85
C) 0.15
D) 0.60
0.60
3
Fill in the blank. A(n) ______ is a process that leads to a single outcome that cannot be predicted with certainty.
A) experiment
B) event
C) sample point
D) sample space
A) experiment
B) event
C) sample point
D) sample space
A
4
In any experiment with exactly four sample points in the sample space, the probability of each sample point is .25.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
5
Which number could be the probability of an event that rarely occurs?
A) .01
B) -.01
C) .51
D) .99
A) .01
B) -.01
C) .51
D) .99

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
6
An experiment consists of randomly choosing a number between 1 and 10. Let E be the event that the number chosen is even. List the sample points in E.
A) {2, 4, 6, 8, 10}
B) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
C) {1, 3, 5, 7, 9}
D) {5}
A) {2, 4, 6, 8, 10}
B) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
C) {1, 3, 5, 7, 9}
D) {5}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following assignments of probabilities to the sample points A, B, and C is valid if A, B, and C are the only sample points in the experiment? 


Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
8
An experiment consists of rolling two dice and summing the resulting values. Which of the following is not a sample point for this experiment?
A) 1
B) 2
C) 6
D) 7
A) 1
B) 2
C) 6
D) 7

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
9
A statistical experiment can be almost any act of observation as long as the outcome is uncertain.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
10
The outcome of an experiment is the number of resulting heads when a nickel and a dime are flipped simultaneously. What is the sample space for this experiment?
A) {0, 1, 2}
B) {HH, HT, TT}
C) {HH, HT, TH, TT}
D) {nickel, dime}
A) {0, 1, 2}
B) {HH, HT, TT}
C) {HH, HT, TH, TT}
D) {nickel, dime}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
11
Which number could be the probability of an event that occurs about as often as it does not occur?
A) .51
B) -.51
C) 0
D) 1
A) .51
B) -.51
C) 0
D) 1

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
12
Suppose that an experiment has five equally likely outcomes. What probability is assigned to each of the sample points?
A) .2
B) .5
C) .05
D) 1
A) .2
B) .5
C) .05
D) 1

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
13
A bag of candy was opened and the number of pieces was counted. The results are shown in the table below: List the sample space for this problem.
A) {25, 20, 20, 15, 10, 10}
B) {0.25, 0.20, 0.20, 0.15, 0.10, 0.10}
C) {Red, Brown, Green, Blue, Yellow, Orange}
D) {Red}
A) {25, 20, 20, 15, 10, 10}
B) {0.25, 0.20, 0.20, 0.15, 0.10, 0.10}
C) {Red, Brown, Green, Blue, Yellow, Orange}
D) {Red}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
14
Which number could be the probability of an event that is almost certain to occur?
A) .99
B) 1.01
C) .51
D) .01
A) .99
B) 1.01
C) .51
D) .01

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
15
If sample points A, B, C, and D are the only possible outcomes of an experiment, find the probability of D using the table below. . 


Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
16
Fill in the blank. A(n) __________ is the most basic outcome of an experiment.
A) sample point
B) event
C) experiment
D) sample space
A) sample point
B) event
C) experiment
D) sample space

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
17
The probability of a sample point is usually taken to be the relative frequency of the occurrence of the sample point in a very long series of repetitions of the experiment.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
18
Fill in the blank. A(n) __________ is a collection of sample points.
A) event
B) Venn diagram
C) sample space
D) experiment
A) event
B) Venn diagram
C) sample space
D) experiment

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
19
Fill in the blank. The __________ is the collection of all the sample points in an experiment.
A) sample space
B) Venn diagram
C) event
D) union
A) sample space
B) Venn diagram
C) event
D) union

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
20
In some experiments, we assign subjective probabilities, which can be interpreted as our degree of belief in the outcome.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
21
The probability of an event can be calculated by finding the sum of the probabilities of the individual sample points in the event and dividing by the number of sample points in the event.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
22
In a sample of 750 of its online customers, a department store found that 420 were men. Use this information to estimate the probability that a randomly selected online customer is a man.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
23
A college has 85 male and 75 female fulltime faculty members. Suppose one fulltime faculty member is selected at random and the faculty member's gender is observed. a. List the sample points for this experiment. b. Assign probabilities to the sample points.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
24
An event may contain sample points that are not in the original sample space of the experiment. For example, the experiment of rolling two dice has the following sample space: {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)} However, the event of rolling a sum of at least 11 on the two dice is {11, 12}.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
25
A hospital reports that two patients have been admitted who have contracted Crohn's disease. Suppose our experiment consists of observing whether each patient survives or dies as a result of the disease. The simple events and probabilities of their occurrences are shown in the table (where S in the first position means that patient 1 survives, D in the first position means that patient 1 dies, etc.). 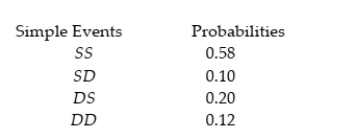 Find the probability that neither patient survives.
Find the probability that neither patient survives.
 Find the probability that neither patient survives.
Find the probability that neither patient survives.
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
26
An experiment consists of randomly choosing a number between 1 and 10. Let A be the event that the number chosen is less than or equal to 7. List the sample points in A.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
27
An economy pack of highlighters contains 12 yellow, 6 blue, 4 green, and 3 orange highlighters. An experiment consists of randomly selecting one of the highlighters. Find the probability that a blue highlighter is chosen.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
28
Probabilities of different types of vehicle-to-vehicle accidents are shown below: Find the probability that an accident involves a car.
A) 0.84
B) 0.66
C) 0.18
D) 0.16
A) 0.84
B) 0.66
C) 0.18
D) 0.16

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
29
At a community college with 500 students, 120 students are age 30 or older. Find the probability that a randomly selected student is age 30 or older.
A) .24
B) .76
C) .12
D) .30
A) .24
B) .76
C) .12
D) .30

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
30
A clothing vendor estimates that 78 out of every 100 of its online customers do not live within 50 miles of one of its physical stores. Using this estimate, what is the probability that a randomly selected online customer does not live within 50 miles of a physical store?
A) .78
B) .22
C) .50
D) .28
A) .78
B) .22
C) .50
D) .28

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
31
The manager of a warehouse club estimates that 7 out of 10 customers will donate a dollar to help a children's hospital during an annual drive to benefit the hospital. Using the manager's estimate, what is the probability that a randomly selected customer will donate a dollar?

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
32
A bag of candy was opened and the number of pieces was counted. The results are shown in the table below: Find the probability that a randomly selected piece is either yellow or orange in color.
A) 20
B) 0.20
C) 10
D) 0.10
A) 20
B) 0.20
C) 10
D) 0.10

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
33
A music store has 8 male and 12 female employees. Suppose one employee is selected at random and the employee's gender is observed. List the sample points for this experiment, and assign probabilities to the sample points.
A) {male, female}; P(male) = .4 and P(female) = .6
B) {male, female}; P(male) = .8 and P(female) = .12
C) {8, 12}; P(8) = .5 and P(12) = .6
D) {8, 12}; P(8) = .8 and P(12) = .12
A) {male, female}; P(male) = .4 and P(female) = .6
B) {male, female}; P(male) = .8 and P(female) = .12
C) {8, 12}; P(8) = .5 and P(12) = .6
D) {8, 12}; P(8) = .8 and P(12) = .12

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
34
A hospital reports that two patients have been admitted who have contracted Crohn's disease. Suppose our experiment consists of observing whether each patient survives or dies as a result of the disease. The simple events and probabilities of their occurrences are shown in the table (where S in the first position means that patient 1 survives, D in the first position means that patient 1 dies, etc.). Find the probability that both patients survive.
A) 0.52
B) 0.2704
C) 0.14
D) 0.34
A) 0.52
B) 0.2704
C) 0.14
D) 0.34

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose that an experiment has eight equally likely outcomes. What probability is assigned to each of the sample points?

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
37
The accompanying Venn diagram describes the sample space of a particular experiment and events A and B. Suppose the sample points are equally likely. Find P(A) and P(B). 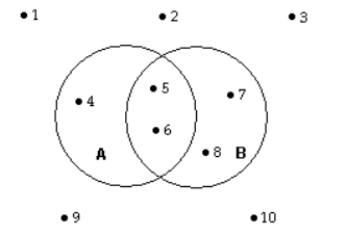


Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
38
A package of self-sticking notepads contains 6 yellow, 6 blue, 6 green, and 6 pink notepads. An experiment consists of randomly selecting one of the notepads and recording its color. Find the sample space for the experiment.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
39
A hospital reports that two patients have been admitted who have contracted Crohn's disease. Suppose our experiment consists of observing whether each patient survives or dies as a result of the disease. The simple events and probabilities of their occurrences are shown in the table (where S in the first position means that patient 1 survives, D in the first position means that patient 1 dies, etc.). Find the probability that at least one of the patients does not survive.
A) 0.41
B) 0.21
C) 0.20
D) 0.11
A) 0.41
B) 0.21
C) 0.20
D) 0.11

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
40
At a small private college with 800 students, 240 students receive some form of government-sponsored financial aid. Find the probability that a randomly selected student receives some form of government-sponsored financial aid.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
41
The table shows the number of each type of book found at an online auction site during a recent search. Suppose that Juanita randomly chose one book to bid on and then noted its type. 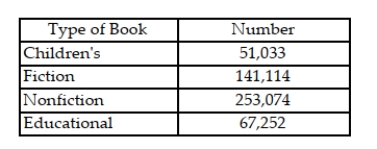 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the book was nonfiction or educational?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the book was nonfiction or educational?
 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the book was nonfiction or educational?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the book was nonfiction or educational?
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
42
The table displays the probabilities for each of the outcomes when three fair coins are tossed and the number of heads is counted. Find the probability that the number of heads on a single toss of the three coins is at most 2.
A) .875
B) .125
C) .500
D) .750
A) .875
B) .125
C) .500
D) .750

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
43
An experiment consists of randomly choosing a number between 1 and 10. Let E be the event that the number chosen is even. Assuming that each of the numbers between 1 and 10 is equally likely to be chosen, find P(E).
A) .5
B) .1
C) .2
D) .8
A) .5
B) .1
C) .2
D) .8

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
44
The table shows the number of each car sold in the United States in June. Suppose the sales record for one of these cars is randomly selected and the type of car is identified. 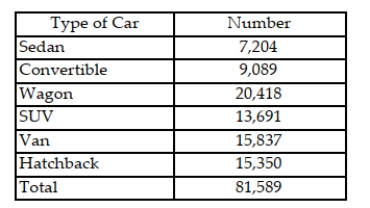 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the car was a Van or an SUV?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the car was a Van or an SUV?
 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the car was a Van or an SUV?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the car was a Van or an SUV?
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
45
The data show the total number of medals (gold, silver, and bronze) won by each country winning at least one gold medal in the Winter Olympics. Suppose that one of the countries represented is chosen at random and the total numbers of medals won by that country is noted. 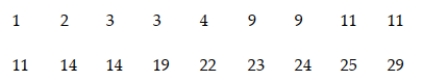 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the country won at least 20 total medals?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the country won at least 20 total medals?
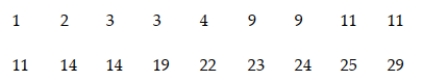 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the country won at least 20 total medals?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the country won at least 20 total medals?
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
46
The table displays the probabilities for each of the six outcomes when rolling a particular unfair die. Find the probability that the number rolled on a single roll of this die is less than 4.
A) .3
B) .2
C) .5
D) .7
A) .3
B) .2
C) .5
D) .7

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
47
Three companies (A, B, and C) are to be ranked first, second, and third in a list of companies with the highest customer satisfaction. a. List all the possible sets of rankings for these top three companies. b. Assuming that all sets of rankings are equally likely, what is the probability that Company A will be ranked first, Company B second, and Company C third? c. Assuming that all sets of rankings are equally likely, what is the probability that Company B will be ranked first?

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
48
A) 1
B) 6
C) 7
D) 720

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
49
In an exit poll, 45% of voters said that the main issue affecting their choices of candidates was the economy, 35% said national security, and the remaining 20% were not sure. Suppose we select one of the voters who participated in the exit poll at random and ask for the main issue affecting his or her choices of candidates. a. List the sample points for this experiment. b. Assign reasonable probabilities to the sample points. c. Find the probability that the main issue affecting his or her choices was either the economy or national security.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
50
A) 9
B) 8
C) 362,880
D) 1

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
51
n = 3, N = 8
A) 56
B) 336
C) 3
D) 120
A) 56
B) 336
C) 3
D) 120

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
52
The data below show the types of medals won by athletes representing the United States in the Winter Olympics. Suppose that one medal is chosen at random and the type of medal noted.  a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the medal was not bronze?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the medal was not bronze?
 a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the medal was not bronze?
a. List the sample points for this experiment. b. Find the probability of each sample point. c. What is the probability that the medal was not bronze?
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
53
Two chips are drawn at random and without replacement from a bag containing four blue chips and three red chips. Find the probability of drawing two red chips. 


Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
54
Two chips are drawn at random and without replacement from a bag containing three blue chips and one red chip. a. List the sample points for this experiment. b. Assign probabilities to the sample points. c. Find the probability of the event A = {Two blue chips are drawn}. d. Find the probability of the event B = {A blue chip and a red chip are drawn}. e. Find the probability of the event C = {Two red chips are drawn}.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
55
A) 45
B) 90
C) 19
D) 8

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
56
At a certain university, one out of every 20 students is enrolled in a statistics course. If one student at the university is chosen at random, what is the probability that the student is enrolled in a statistics course? 


Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
57
The following data represent the scores of 50 students on a statistics exam. Suppose that one of the 50 students is chosen at random and that student's score is noted. 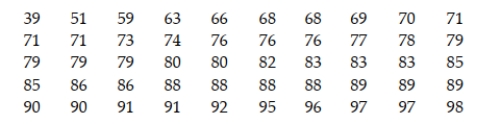 a. What is the probability that the student's score is 88? b. What is the probability that the student's score is less than 60? c. What is the probability that the student's score is between 70 and 79, inclusive?
a. What is the probability that the student's score is 88? b. What is the probability that the student's score is less than 60? c. What is the probability that the student's score is between 70 and 79, inclusive?
 a. What is the probability that the student's score is 88? b. What is the probability that the student's score is less than 60? c. What is the probability that the student's score is between 70 and 79, inclusive?
a. What is the probability that the student's score is 88? b. What is the probability that the student's score is less than 60? c. What is the probability that the student's score is between 70 and 79, inclusive?
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
58
A) 28
B) 56
C) 4
D) 720

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
59
A) 1
B) 7
C) 8
D) 5040

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
60
Three fair coins are tossed and either heads (H) or tails (T) is observed for each coin. a. List the sample points for this experiment. b. Assign probabilities to the sample points. c. Find the probability of the event A = {Three heads are observed}. d. Find the probability of the event B = {Exactly two heads are observed}. e. Find the probability of the event C = {At least two heads are observed}.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
61
A number between 1 and 10, inclusive, is randomly chosen. Events A and B are defined as follows. A: {The number is even} B: {The number is less than 7} Identify the sample points in the event A ∪ B.
A) {1, 2, 3, 4, 5, 6, 8, 10}
B) {2, 4, 6}
C) {1, 2, 3, 4, 5, 6, 7, 8, 10}
D) {1, 2, 3, 4, 5, 6, 7, 9}
A) {1, 2, 3, 4, 5, 6, 8, 10}
B) {2, 4, 6}
C) {1, 2, 3, 4, 5, 6, 7, 8, 10}
D) {1, 2, 3, 4, 5, 6, 7, 9}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
62
Evaluate .
A) 28
B) 16
C) 56
D) 4
A) 28
B) 16
C) 56
D) 4

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
63
A pair of fair dice is tossed. Events A and B are defined as follows. A: {The sum of the numbers on the dice is 3} B: {At least one of the dice shows a 2} Identify the sample points in the event A ∩ B.
A) {(1, 2), (2, 1)}
B) {(1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}
C) {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)}
D) {(2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}
A) {(1, 2), (2, 1)}
B) {(1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}
C) {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)}
D) {(2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
64
Compute 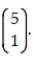 .
.
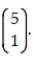 .
.
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
65
Compute 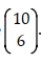 .
.
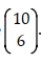 .
.
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
66
Evaluate .
A) 1
B) 6
C) 0
D) undefined
A) 1
B) 6
C) 0
D) undefined

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
67
A pair of fair dice is tossed. Events A and B are defined as follows. A: {The sum of the numbers on the dice is 3} B: {At least one of the dice shows a 2} Identify the sample points in the event A ∪ B.
A) {(1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}
B) {(1, 2), (2, 1)}
C) {(1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)}
D) {(2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}
A) {(1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}
B) {(1, 2), (2, 1)}
C) {(1, 2), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)}
D) {(2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (4, 2), (5, 2), (6, 2)}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
68
Compute the number of ways you can select n elements from N elements for n = 6 and N = 15.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
69
Compute the number of ways you can select 3 elements from 7 elements.
A) 35
B) 21
C) 10
D) 343
A) 35
B) 21
C) 10
D) 343

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
70
The quantity 0! is defined to be equal to 0.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
71
In how many ways can a manager choose 3 of his 8 employees to work overtime helping with inventory?

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate .
A) 1
B) 7
C) 14
D) 49
A) 1
B) 7
C) 14
D) 49

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
73
The combinations rule applies to situations in which the experiment calls for selecting n elements from a total of N elements, without replacing each element before the next is selected.

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
74
Which quantity is represented on the screen below? 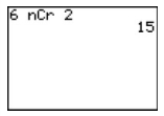
A) The number of ways two coins can be chosen from six coins
B) The number of sample points when a die is rolled and a coin is flipped
C) The number of ways two dice can be rolled
D) The number of sample points when a coin is flipped six times

A) The number of ways two coins can be chosen from six coins
B) The number of sample points when a die is rolled and a coin is flipped
C) The number of ways two dice can be rolled
D) The number of sample points when a coin is flipped six times

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
75
n = 4, N = 10
A) 210
B) 5040
C) 34
D) 6
A) 210
B) 5040
C) 34
D) 6

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
76
Kim submitted a list of 12 movies to an online movie rental company. The company will choose 3 of the movies and ship them to her. If all movies are equally likely to be chosen, what is the probability that Kim will receive the three movies that she most wants to watch? Express the probability as a fraction.  Answer the question True or False.
Answer the question True or False.
 Answer the question True or False.
Answer the question True or False.
Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
77
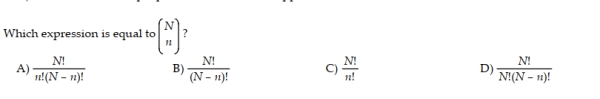

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
78
A number between 1 and 10, inclusive, is randomly chosen. Events A and B are defined as follows. A: {The number is even} B: {The number is less than 7} Identify the sample points in the event A ∩ B.
A) {2, 4, 6}
B) {1, 2, 3, 4, 5, 6, 8, 10}
C) {1, 2, 3, 4, 5, 6, 7, 8, 10}
D) {1, 2, 3, 4, 5, 6, 7, 9}
A) {2, 4, 6}
B) {1, 2, 3, 4, 5, 6, 8, 10}
C) {1, 2, 3, 4, 5, 6, 7, 8, 10}
D) {1, 2, 3, 4, 5, 6, 7, 9}

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
79
There are 10 movies that Greg would like to rent but the store only allows him to have 4 movies at one time. In how many ways can Greg choose 4 of the 10 movies?
A) 210
B) 40
C) 10,000
D) 5040
A) 210
B) 40
C) 10,000
D) 5040

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck
80
The manager of an advertising department has asked her creative team to propose six new ideas for an advertising campaign for a major client. She will choose three of the six proposals to present to the client. (We will refer to the six proposals as A, B, C, D, E, and F.) a. In how many ways can the manager select the three of the six proposals? List the possibilities. b. It is unlikely that the manager will randomly select three of the six proposals, but if she does what is the probability that she selects proposals A, D, and E?

Unlock Deck
Unlock for access to all 283 flashcards in this deck.
Unlock Deck
k this deck



